Aufgaben:Exercise 3.6Z:Optimum Nyquist Equalizer for Exponential Pulse

• Return to book

Beidseitiger Exponentialimpuls

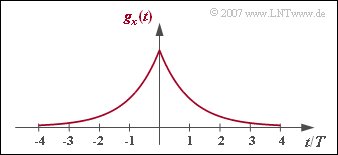
Wie in Aufgabe 3.6 betrachten wir wieder den optimalen Nyquistentzerrer, wobei nun als Eingangsimpuls $g_x(t)$ eine beidseitig abfallende Exponentialfunktion anliegt:

$$g_x(t) = {\rm e }^{ - |t|/T}\hspace{0.05cm}.$$

Durch ein Transversalfilter $N$–ter Ordnung mit der Impulsantwort

$$h_{\rm TF}(t) = \sum_{\lambda = -N}^{+N} k_\lambda \cdot \delta(t - \lambda \cdot T)$$

ist es immer möglich, dass der Ausgangsimpuls $g_y(t)$ Nulldurchgänge bei $t/T = ±1, \ ... \ , \ t/T = ±N$ aufweist und $g_y(t = 0) = 1$ ist. Im allgemeinen Fall führen dann allerdings die Vorläufer und Nachläufer mit $| \nu | > N$ zu Impulsinterferenzen.

Hinweis:

• Die Aufgabe bezieht sich auf das Kapitel Lineare Nyquistentzerrung.

Fragebogen

1

Geben Sie die Signalwerte $g_x(\nu) = g_x(t = \nu T)$ bei Vielfachen von $T$ an.

$g_x(0)$ =

$g_x(1)$ =

$g_x(2)$ =

2

Berechnen Sie die optimalen Filterkoeffizienten für $N = 1$.

$k_0$ =

$k_1$ =

3

Berechnen Sie die Ausgangswerte $g_2 = g_{\rm \nu}(t = 2T)$ und $g_3 = g_{\rm \nu}(t = 3T)$.

$g_2$ =

$g_3(0)$ =

4

Welche der nachfolgenden Aussagen sind zutreffend?

	Beim gegebenen Eingangsimpuls $g_x(t)$ ist mit einem Transversalfilter zweiter Ordnung keine Verbesserung möglich.
	Die erste Aussage ist unabhängig vom Eingangsimpuls $g_x(t)$.
	Beim gegebenen Eingangsimpuls ergibt sich mit einem unendlichen Transversalfilter eine weitere Verbesserung.

Musterlösung

Solution

(1)  (2)  (3)  (4)  (5)