Aufgaben:Exercise 3.8Z: Optimal Detection Time for DFE

• Return to book

Tabelle der Grundimpulswerte

Wir betrachten wie in der Aufgabe 3.8 das bipolare Binärsystem mit Entscheidungsrückkopplung. Im Englischen bezeichnet man diese Konstellation als Decision Feedback Equalization (DFE).

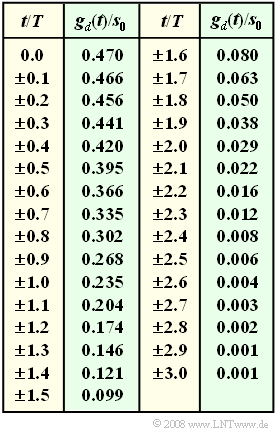
Der vorentzerrte Grundimpuls $g_d(t)$ am Eingang der DFE entspricht der Rechteckantwort eines Gaußtiefpasses mit der Grenzfrequenz $f_{\rm G} \cdot T = 0.25$.

In der Tabelle sind die auf $s_0$ normierten Abtastwerte von $g_d(t)$ angegeben. Auf der Angabenseite zu Aufgabe 3.8 ist $g_d(t)$ skizziert.

Bei der idealen DFE wird ein Kompensationsimpuls $g_w(t)$ gebildet, der für alle Zeiten $t ≥ T_{\rm D} + T_{\rm V}$ genau gleich dem Eingangsimpuls $g_d(t)$ ist, so dass für den korrigierten Grundimpuls gilt:

$$g_k(t) \ = \ g_d(t) - g_w(t) = \ \left\{ \begin{array}{c} g_d(t) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\\ {\rm{f\ddot{u}r}} \\ \end{array} \begin{array}{*{20}c} t < T_{\rm D} + T_{\rm V}, \\ t \ge T_{\rm D} + T_{\rm V}, \\ \end{array}$$

Hierbei bezeichnet $T_{\rm D}$ den Detektionszeitpunkt, der eine optimierbare Systemgröße darstellt. $T_{\rm D} = 0$ bedeutet eine Symboldetektion in Impulsmitte.

Bei einem System mit DFE ist jedoch $g_k(t)$ stark unsymmetrisch, so dass ein Detektionszeitpunkt $T_{\rm D} < 0$ günstiger ist. Die Verzögerungszeit $T_{\rm V} = T/2$ gibt an, dass die DFE erst eine halbe Symboldauer nach der Detektion wirksam wird. Zur Lösung dieser Aufgabe ist $T_{\rm V}$ allerdings nicht relevant.

Eine aufwandsgünstige Realisierung der DFE ist mit einem Laufzeitfilter möglich, wobei die Filterordnung bei dem gegebenen Grundimpuls mindestens $N = 3$ betragen muss. Die Filterkoeffizienten sind dabei wie folgt zu wählen:

$$k_1 = g_d(T_{\rm D} + T),\hspace{0.2cm}k_2 = g_d(T_{\rm D} + 2T),\hspace{0.2cm}k_3 = g_d(T_{\rm D} + 3T) \hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe behandelt die theoretischen Grundlagen des Kapitels Entscheidungsrückkopplung.
• Beachten Sie auch, dass die Entscheidungsrückkopplung nicht mit einer Erhöhung der Rauschleistung verbunden ist, so dass eine Vergrößerung der (halben) Augenöffnung um den Faktor $K$ gleichzeitig einen Störabstandsgewinn von $20 \cdot {\rm lg} \, K$ zur Folge hat.
• Der vorentzerrte Grundimpuls $g_d(t)$ am Eingang der DFE entspricht der Rechteckantwort eines Gaußtiefpasses mit der Grenzfrequenz $f_{\rm G} \cdot T = 0.25$. In der Tabelle sind die auf $s_0$ normierten Abtastwerte von $g_d(t)$ angegeben. Auf der Angabenseite zu Aufgabe A3.8 ist $g_d(t)$ skizziert.

Fragebogen

1

Berechnen Sie die halbe Augenöffnung für $T_{\rm D} = 0$ und ideale DFE.

$100\% \ {\rm DFE} \text{:} \hspace{0.2cm} \ddot{o}(T_{\rm D} = 0)/(2s_0)$ =

2

Wie müssen hierzu die Koeffizienten des Laufzeitfilters eingestellt werden?

$k_1$ =

$k_2$ =

$k_3$ =

3

Es gelte weiter $T_{\rm D} = 0$. Welche (halbe) Augenöffnung ergibt sich, wenn die DFE die Nachläufer nur zu $50 \%$ kompensiert?

$50\% \ {\rm DFE} \text{:} \hspace{0.2cm} \ddot{o}(T_{\rm D} = 0)/(2s_0)$ =

4

Bestimmen Sie den optimalen Detektionszeitpunkt und die Augenöffnung bei idealer DFE.

$D_{\rm D, \ opt}/T$ =

$100\% \ {\rm DFE} \text{:} \hspace{0.2cm} \ddot{o}(T_{\rm D} = 0)/(2s_0)$ =

5

Multiple-Choice Frage

	Falsch
	Richtig

6

Input-Box Frage

$\alpha$ =

Musterlösung

Solution

(1)  (2)  (3)  (4)  (5)  (6)