Aufgaben:Exercise 3.11Z: Metric and Accumutated Metric

• Return to book

Berechnung der minimalen Gesamtfehlergrößen

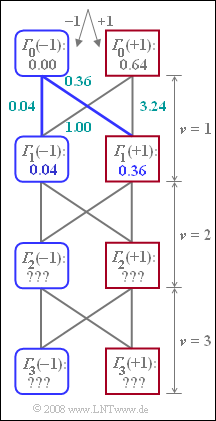
Für die in der Aufgabe A3.11 behandelte Maximum–Likelihood–Konstellation mit bipolaren Amplitudenkoeffizient $a_{\rm \nu} ∈ \{+1, –1\}$ sollen die Fehlergrößen $\epsilon_{\rm \nu}(i)$ und die minimalen Gesamtfehlergrößen ${\it \Gamma}_{\rm \nu}(–1)$, ${\it \Gamma}_{\rm \nu}(+1)$ ermittelt werden.

Der Grundimpuls ist durch die beiden Werte $g_0$ und $g_{\rm –1}$ gegeben. Diese können ebenso wie die Detektionsabtastwerte $d_0$ und $d_1$ aus den nachfolgenden Berechnungen für die Fehlergrößen $\epsilon_{\rm \nu}(i)$ zu den Zeitpunkten $\nu = 0$ und $\nu = 1$ entnommen werden. Anzumerken ist, dass vor der eigentlichen Nachricht ($a_1$, $a_2$, $a_3$) stets das Symbol $a_0 = 0$ gesendet wird. Für den Zeitpunkt $\nu = 0$ gilt:

$$\varepsilon_{0}(+1) \ = \ [-0.4- 0.4]^2=0.64 \hspace{0.05cm},$$

$$\varepsilon_{0}(-1) \ = \ [-0.4+ 0.4]^2=0.00 \hspace{0.05cm}.$$

Daraus könnte bereits zum Zeitpunkt $\nu = 0$ geschlossen werden, dass mit großer Wahrscheinlichkeit $a_1 = \ –1$ ist. Für den Zeitpunkt $\nu = 1$ ergeben sich folgende Fehlergrößen:

$$\varepsilon_{1}(+1, +1) \ = \ [-0.8- 0.6 -0.4]^2=3.24

\hspace{0.05cm},$$

$$\varepsilon_{1}(+1, -1) \ = \ [-0.8- 0.6 +0.4]^2=1.00

\hspace{0.05cm},$$

$$\varepsilon_{1}(-1, +1) \ = \ [-0.8+ 0.6 -0.4]^2=0.36

\hspace{0.05cm},$$

$$ \varepsilon_{1}(-1, -1) \ = \ [-0.8+ 0.6 +0.4]^2=0.04

 \hspace{0.05cm}.$$

Die minimalen Gesamtfehlergrößen ${\it \Gamma}_{\rm \nu}(–1)$ und ${\it \Gamma}_{\rm \nu}(+1)$, die mit diesen sechs Fehlergrößen berechnet werden können, sind bereits in der Grafik eingezeichnet. Die weiteren Detektionsabtastwerte sind

$$d_{2}=0.1 \hspace{0.05cm},\hspace{0.2cm}

d_{3}=0.5 \hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Themengebiet von Kapitel Decision Feedback Equalization mit Laufzeitfilter.
• Alle Größen sind hier normiert zu verstehen.
• Die hier angesprochene Thematik wird auch im folgenden Interaktionsmodul behandelt: Eigenschaften des Viterbi–Empfängers.

Fragebogen

1 Von welchen Detektionsabtastwerten $d_0$ und $d_1$ wurde ausgegangen?

$d_0$ =

$d_1$ =

2 Welche Grundimpulswerte wurden dabei vorausgesetzt?

$g_0$ =

$g_{\rm –1}$ =

3 Welche der aufgeführten Detektionsabtastwerte sind für $\nu ≥ 1$ möglich?

	$±0.2,$
	$±0.4,$
	$±0.6,$
	$±1.0.$

4 Gegen Sie die minimalen Gesamtfehlergrößen für die Zeit $\nu = 2$ an ($d_2 = 0.1$).

${\it \Gamma}_2(+1)$ =

${\it \Gamma}_2(–1)$ =

5 Berechnen Sie die minimalen Gesamtfehlergrößen für die Zeit $\nu = 3$ ($d_3 = 0.5$).

${\it \Gamma}_3(+1)$ =

${\it \Gamma}_3(–1)$ =

Musterlösung

Solution

(1)  (2)  (3)  (4)  (5)