Aufgaben:Exercise 4.06Z: Signal Space Constellations

• Return to book

Drei Signalraumkonstellationen

Die (mittlere) Fehlerwahrscheinlichkeit eines optimalen Binärsystems lautet:

$$p_{\rm S} = {\rm Pr}({ \cal E} ) = {\rm Q} \left ( \frac{d/2}{\sigma_n} \right )\hspace{0.05cm}.$$

Hierzu ist anzumerken:

• ${\rm Q}(x)$ bezeichnet die komplementäre Gaußsche Fehlerfunktion (Definition und Approximation):

$${\rm Q}(x) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{\sqrt{2\pi}} \int_{x}^{\infty} {\rm e}^{-u^2/2} \,{\rm d} u \approx$$

$$\hspace{-0.1cm} \ \approx \ \hspace{-0.1cm} \frac{1}{\sqrt{2\pi} \cdot x} \cdot {\rm e}^{-x^2/2} \hspace{0.05cm}.$$

• $d$ gibt den Abstand der beiden Sendesignalpunkte $s_0$ und $s_1$ im vorgegebenen Vektorraum an:

$$d = \sqrt{ || \boldsymbol{ s }_1 - \boldsymbol{ s }_0||^2} \hspace{0.05cm}.$$

• $\sigma_n^2$ ist die Varianz des AWGN–Rauschens nach dem Detektor, der zum Beispiel als Matched–Filter realisiert sein kann. Es gelte $\sigma_n^2 = N_0/2$.

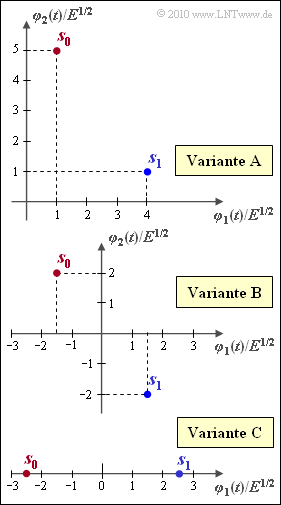
Durch die Grafik sind drei unterschiedliche Signalraumkonstellationen gegeben, nämlich

• Variante A : $s_0 = (+1, \ \, +5), \hspace{0.4cm} s_1 = (+4, \ \, +1)$,
• Variante B : $s_0 = (–1.5, \ \, +2), \, s_1 = (+1.5, \ \, –2)$,
• Variante C : $s_0 = (–2.5, \ \, 0), \hspace{0.65cm} s_1 = (+2.5, \ \, 0)$.

Die jeweils mittlere Energie pro Symbol ($E_{\rm S}$) kann nach folgender Gleichung berechnet werden:

$$E_{\rm S} = {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_0) \cdot || \boldsymbol{ s }_0||^2 + {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_1) \cdot || \boldsymbol{ s }_1||^2\hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Themengebiet von Kapitel Approximation der Fehlerwahrscheinlichkeit.
• Wenn bei einer Teilaufgabe keine anderslautende Angabe gemacht ist, so kann von gleichwahrscheinlichen Symbolen ausgegangen werden:

$${\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_0) = {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_1) = 0.5\hspace{0.05cm}.$$

• Die Normierungsenergie $E$ ist hier stillschweigend zu $1$ gesetzt.

Fragebogen

1

Welche Voraussetzungen müssen unbedingt (auf jeden Fall) erfüllt sein, damit die angegebene Fehlerwahrscheinlichkeitsgleichung gilt?

	additives weißes Gaußsches Rauschen mit Varianz $\sigma_n^2$,
	optimaler Binärempfänger,
	Entscheidungsgrenze in der Mitte zwischen den Symbolen,
	gleischwahrscheinliche Symbole $s_0$ und $s_1$.

2

Welche Aussage gilt für die Fehlerwahrscheinlichkeit mit $\sigma_n^2 = E$?

	Die kleinste Fehlerwahrscheinlichkeit tritt bei Variante A auf.
	Die kleinste Fehlerwahrscheinlichkeit tritt bei Variante B auf.
	Die kleinste Fehlerwahrscheinlichkeit tritt bei Variante C auf.
	Alle Varianten zeigen gleiches Fehlerverhalten.

3

Geben Sie die Fehlerwahrscheinlichkeit für die Variante A mit $\sigma_n^2 = E$ an. Sie können ${\rm Q}(x)$ entsprechend der Näherung berechnen.

$\sigma_n^2 = E, \ {\rm Variante} \ A \text{:} \hspace{0.2cm} p_{\rm S}$ = $\ \cdot 10^{\rm –2}$

4

Es gelte $N_0 = 2 \cdot 10^{\rm –6} \ {\rm W/Hz}$, $E_{\rm S} = 6.25 \cdot 10^{\rm –6} \ \rm Ws$. Welche Wahrscheinlichkeit ergibt sich für die Variante C bei gleichwahrscheinlichen Symbolen?

${\rm Variante} \ C \text{:} \hspace{0.2cm} p_{\rm S}$ = $\ \cdot 10^{\rm –2}$

5

Welche Fehlerwahrscheinlichkeit ergibt sich bei gleichen Voraussetzungen für die Variante B?

${\rm Variante} \ B \text{:} \hspace{0.2cm} p_{\rm S}$ = $\ \cdot 10^{\rm –2}$

6

Wie groß ist bei der Variante A die mittlere Energie pro Symbol ($E_{\rm S}$) zu wählen, um die gleiche Fehlerwahrscheinlichkeit wie bei System C zu erhalten?

${\rm Variante \ \it A} \text{:} \hspace{0.2cm} E_{\rm S}$ = $\ \cdot 10^{\rm –6} \ \rm Ws$

Musterlösung

Solution

(1)  Die drei erstgenannten Voraussetzungen müssen auf jeden Fall erfüllt sein. Die Gleichung gilt dann unabhängig von den Auftrittswahrscheinlichkeiten. Im Fall ${\rm Pr}(\boldsymbol{s} = \boldsymbol{s}_0) ≠ {\rm Pr}(\boldsymbol{s} = \boldsymbol{s}_1)$ kann durch eine Verschiebung der Entscheiderschwelle eine kleinere Fehlerwahrscheinlichkeit erzielt werden.

(2)  Der Rauscheffektivwert $\sigma_n$ und damit auch die Signalenergie $E = \sigma_n^2$ sind für alle drei betrachteten Varianten gleich. Gleiches gilt für die Distanz der Signalraumpunkte. Für die Variante A gilt zum Beispiel:

$$d = \sqrt{ || \boldsymbol{ s }_1 - \boldsymbol{ s }_0||^2} = \sqrt{ E \cdot (4-1)^2 + E \cdot (1-5)^2} = 5 \cdot \sqrt{E}\hspace{0.05cm}.$$

Durch die Verschiebung des Koordinatensystems ändert sich am Absand zwischen $\boldsymbol{s}_0$ und $\boldsymbol{s}_1$ nichts (Variante B), und auch bei Variante C (nach Drehung) ergibt sich der gleiche Abstand.

Richtig ist also der Lösungsvorschlag 4. Durch eine Drehung des Koordinatensystems kann man bei einem Binärsystem ($M = 2$) stets mit einer Basisfunktion ($N = 1$) auskommen. Da das zweidimensionale Rauschen zirkulär symmetrisch ist  ⇒  gleiche Streuung $\sigma_n$ in alle Richtungen, kann auch der Rauschterm wie im Kapitel Fehlerwahrscheinlichkeit bei Basisbandübertragung eindimensional beschrieben werden.

(3)  Für alle hier betrachteten Varianten, also auch für die Variante A, gilt:

$$p_{\rm S} = {\rm Pr}({ \cal E} ) = {\rm Q} \left ( \frac{d/2}{\sigma_n} \right )= {\rm Q} \left ( \frac{5/2 \cdot \sqrt{E}}{\sigma_n} \right ) = {\rm Q}(2.5)\hspace{0.05cm}.$$

Mit der angegebenen Näherung erhält man

$$p_{\rm S} = \frac{1}{\sqrt{2\pi} \cdot 2.5} \cdot {\rm e}^{-2.5^2/2} \hspace{0.1cm} \hspace{0.15cm}\underline {\approx 0.7 \cdot 10^{-2}}\hspace{0.05cm}.$$

(4)  Bei der Variante C ergibt sich für die mittlere Energie pro Symbol:

$$E_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_0) \cdot (-2.5 \cdot \sqrt{E})^2 + {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_1) \cdot (+ 2.5 \cdot \sqrt{E})^2 =$$

$$\hspace{-0.1cm} \ = \ \hspace{-0.1cm} \left [ {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_0) + {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_0) \right ] \cdot 6.25 \cdot E = 6.25 \cdot E$$

$$\Rightarrow \hspace{0.3cm} E = \frac {E_{\rm S}}{6.25} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \sqrt{E}= \frac {\sqrt{E_{\rm S}}}{2.5} \hspace{0.05cm}.$$

Setzt man dieses Ergebnis in die unter (3) gefundene Gleichung ein, so erhält man mit $\sigma_n^2 = N_0/2$:

$$p_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Q} \left ( \frac{2.5 \cdot \sqrt{E}}{\sigma_n} \right )= {\rm Q} \left ( \frac{ \sqrt{E_{\rm S}}}{\sigma_n} \right ) = {\rm Q} \left ( \frac{ \sqrt{2 \cdot E_{\rm S}}}{N_0} \right ) =$$

$$\hspace{-0.1cm} \ = \ \hspace{-0.1cm}{\rm Q} \left ( \sqrt{\frac{ 2 \cdot 6.25 \cdot 10^{-6}\,{\rm Ws}}{2 \cdot 10^{-6}\,{\rm W/Hz}}} \right ) ={\rm Q}(2.5) \hspace{0.1cm} \hspace{0.15cm}\underline {\approx 0.7 \cdot 10^{-2}}\hspace{0.05cm}.$$

(5)  Durch die Drehung des Koordinatensystems ändert sich nichts an den Energieverhältnissen. Aus diesem Grund erhält man wieder $p_{\rm S} \ \underline {\approx 0.007}$.

(6)  Bei der Variante A ist die mittlere Energie pro Symbol

$$E_{\rm S} = {1}/{2} \cdot \left [ (1^2 + 5^2) \cdot E + (4^2 + 1^2) \cdot E \right ] = 21.5 \cdot E \hspace{0.05cm}.$$

Der Abstand von der Schwelle, die bei gleichwahrscheinlichen Symbolen in der Mitte zwischen $\boldsymbol{s}_0$ und $\boldsymbol{s}_1$ liegen sollte, ist wie bei den anderen Varianten $d/2 = 2.5 \cdot E^{\rm 1/2}$. Mit $\sigma_n^2 = N_0/2$ erhält man somit die Bestimmungsgleichung:

$$p_{\rm S} = {\rm Q} \left ( \frac{ 2.5 \cdot \sqrt{E}}{\sqrt{N_0/2}} \right ) ={\rm Q}(2.5)\approx 0.7 \cdot 10^{-2}$$

$$\Rightarrow \hspace{0.3cm} \sqrt{\frac {2E}{N_0}} = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \frac {E}{N_0} = 0.5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\frac {E_{\rm S}}{21.5 \cdot N_0} = 0.5$$

$$\Rightarrow \hspace{0.3cm} {E_{\rm S}} = 0.5 \cdot {21.5 \cdot N_0} \hspace{0.1cm} \hspace{0.15cm}\underline { = 21.5 \cdot 10^{-6}\,{\rm Ws}}\hspace{0.05cm}.$$

Das bedeutet: Bei der Variante A ist gegenüber den beiden anderen Symbolen eine um den Faktor 3.44 größere mittlere Symbolenergie $E_{\rm S}$ erforderlich, um die gleiche Fehlerwahrscheinlichkeit $p_{\rm S} = 0.007$ zu erzielen. Das heißt: Diese Signalraumkonstellation ist sehr ungünstig. Es ergibt sich ein sehr großes $E_{\rm S}$, ohne dass gleichzeitig der Abstand $d$ vergrößert wird.

Mit $E_{\rm S} = 6.25 \cdot 10^{\rm –6} \ \rm Ws$ würde sich dagegen $p_{\rm S} = {\rm Q}(2.5/3.44^{\rm 1/2}) \approx {\rm Q}(1.35) \approx 9\%$ ergeben. Das heißt: Die Fehlerwahrscheinlichkeit würde um mehr als eine Zehnerpotenz größer.