Difference between revisions of "Aufgaben:Exercise 4.09Z: Laplace Distributed Noise"
From LNTwww
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Digitalsignalübertragung/Approximation der Fehlerwahrscheinlichkeit}} Datei:P_ID2044__Dig_A_4_9.png|right|frame|Drei verschiedene…“) |
|||
| Line 2: | Line 2: | ||
{{quiz-Header|Buchseite=Digitalsignalübertragung/Approximation der Fehlerwahrscheinlichkeit}} | {{quiz-Header|Buchseite=Digitalsignalübertragung/Approximation der Fehlerwahrscheinlichkeit}} | ||
| − | [[File: | + | [[File:P_ID2042__Dig_Z_4_9.png|right|frame|2D–Laplace–WDF]] |
| + | Wir betrachten zweidimensionales Rauschen $\boldsymbol{n} = (n_1, n_2)$. | ||
| − | + | Die beiden Rauschvariablen sind „<i>independent and identically distributed</i>”, abgekürzt i.i.d., und besitzen beide jeweils eine Laplace–Wahrscheinlichkeitsdichte: | |
| + | :$$p_{n_1}(x) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} K \cdot {\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm} |x|} \hspace{0.05cm},$$ | ||
| + | :$$ p_{n_2}(y) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} K \cdot {\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm} |y|} \hspace{0.05cm}. $$ | ||
| + | Die 2D–Wahrscheinlichkeitsdichtefunktion $p_{\it \boldsymbol{n})(x, y)$ ist in der Grafik dargestellt. Zur Vereinfachung der Schreibweise werden hier die Realisierungen von $n_1$ und $n_2$ mit $x$ und $y$ bezeichnet. | ||
| + | ''Hinweise:'' | ||
| + | * Die Aufgabe bezieht sich auf das Kapitel [[Digitalsignal%C3%BCbertragung/Approximation_der_Fehlerwahrscheinlichkeit| Approximation der Fehlerwahrscheinlichkeit]]. | ||
| + | * Beachten Sie bitte, dass in Teilaufgabe (6) das sich ergebende Integral aufgrund der Betragsbildung in mehrere Teilintegrale aufgespalten werden muss. | ||
| + | * Weiterhin gilt: | ||
| + | :$$\int_{0}^{\infty} x^2 \cdot {\rm e}^{-a \hspace{0.03cm}\cdot \hspace{0.03cm} x} \,{\rm d} x = {2}/{a^3} \hspace{0.05cm}.$$ | ||
| + | |||
| + | ===Fragebogen=== | ||
| + | <quiz display=simple> | ||
| + | {Multiple-Choice | ||
| + | |type="[]"} | ||
| + | + correct | ||
| + | - false | ||
| + | |||
| + | {Input-Box Frage | ||
| + | |type="{}"} | ||
| + | $xyz$ = { 5.4 3% } $ab$ | ||
| + | </quiz> | ||
| + | |||
| + | ===Musterlösung=== | ||
| + | {{ML-Kopf}} | ||
| + | '''(1)''' | ||
| + | '''(2)''' | ||
| + | '''(3)''' | ||
| + | '''(4)''' | ||
| + | '''(5)''' | ||
| + | {{ML-Fuß}} | ||
[[Category:Aufgaben zu Digitalsignalübertragung|^4.3 BER-Approximation^]] | [[Category:Aufgaben zu Digitalsignalübertragung|^4.3 BER-Approximation^]] | ||
Revision as of 09:21, 8 November 2017
Wir betrachten zweidimensionales Rauschen $\boldsymbol{n} = (n_1, n_2)$.
Die beiden Rauschvariablen sind „independent and identically distributed”, abgekürzt i.i.d., und besitzen beide jeweils eine Laplace–Wahrscheinlichkeitsdichte:
- $$p_{n_1}(x) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} K \cdot {\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm} |x|} \hspace{0.05cm},$$
- $$ p_{n_2}(y) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} K \cdot {\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm} |y|} \hspace{0.05cm}. $$
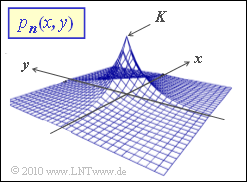
Die 2D–Wahrscheinlichkeitsdichtefunktion $p_{\it \boldsymbol{n})(x, y)$ ist in der Grafik dargestellt. Zur Vereinfachung der Schreibweise werden hier die Realisierungen von $n_1$ und $n_2$ mit $x$ und $y$ bezeichnet.
Hinweise:
- Die Aufgabe bezieht sich auf das Kapitel Approximation der Fehlerwahrscheinlichkeit.
- Beachten Sie bitte, dass in Teilaufgabe (6) das sich ergebende Integral aufgrund der Betragsbildung in mehrere Teilintegrale aufgespalten werden muss.
- Weiterhin gilt:
- $$\int_{0}^{\infty} x^2 \cdot {\rm e}^{-a \hspace{0.03cm}\cdot \hspace{0.03cm} x} \,{\rm d} x = {2}/{a^3} \hspace{0.05cm}.$$
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)