Difference between revisions of "Aufgaben:Exercise 4.17: Non-Coherent On-Off Keying"
| Line 2: | Line 2: | ||
{{quiz-Header|Buchseite=Digitalsignalübertragung/Trägerfrequenzsysteme mit nichtkohärenter Demodulation}} | {{quiz-Header|Buchseite=Digitalsignalübertragung/Trägerfrequenzsysteme mit nichtkohärenter Demodulation}} | ||
| + | [[File:P_ID2078__Dig_A_4_17.png|right|frame|Rayleigh– und Riceverteilung]] | ||
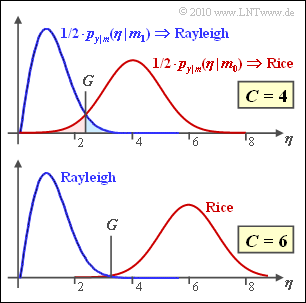
| + | Die Abbildung zeigt die beiden Dichtefunktionen, die sich bei einer nichtkohärenten Demodulation von <i>On–Off–Keying</i> ergeben. Dabei wird vorausgesetzt, dass die zwei OOK–Signalraumpunkte bei $\boldsymbol{s}_0 = C$ (Nachricht $m_0$) und bei $\boldsymbol{s}_1 = 0$ (Nachricht $m_1$) liegen. | ||
| + | |||
| + | Die Symbolfehlerwahrscheinlichkeit dieses Systems wird durch die folgende Gleichung beschrieben: | ||
| + | :$$p_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}({\cal{E}}) = $$ | ||
| + | :$$\hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{ 2} \cdot \int_{0}^{G} p_{y|m} (\eta | m_0) \,{\rm d} \eta | ||
| + | +$$ | ||
| + | :$$ \hspace{-0.1cm} \ + \ \hspace{-0.1cm} {1}/{ 2} \cdot \int_{G}^{\infty} p_{y|m} (\eta | m_1) \,{\rm d} \eta | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | Mit der Streuung $\sigma_n = 1$, die im Folgenden vorausgesetzt wird, lautet die sich für $m = m_1$ ergebende Rayleighverteilung (blaue Kurve): | ||
| + | :$$p_{y|m} (\eta | m_1) = \eta \cdot {\rm e }^{-\eta^2/2} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | Die Riceverteilung (rote Kurve) kann im vorliegenden Fall (wegen $C >> \sigma_n$) durch eine Gaußverteilung angenähert werden: | ||
| + | :$$p_{y|m} (\eta | m_0) = \frac{1}{\sqrt{2\pi}} \cdot {\rm e }^{-(\eta-C)^2/2} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | Die optimale Entscheidergrenze $G_{\rm opt}$ ergibt sich aus dem Schnittpunkt von roter und blauer Kurve. Aus den beiden Skizzen erkennt man, dass $G_{\rm opt}$ von $C$ abhängt. Für die obere Grafik gilt $C = 4$, für die untere $C = 6$. Alle Größen sind normiert und es wird stets $\sigma_n = 1$ vorausgesetzt. | ||
| + | |||
| + | ''Hinweise:'' | ||
| + | * Die Aufgabe gehört zum Themengebiet des Kapitels [[Digitalsignal%C3%BCbertragung/Tr%C3%A4gerfrequenzsysteme_mit_nichtkoh%C3%A4renter_Demodulation| Trägerfrequenzsysteme mit nichtkohärenter Demodulation]]. | ||
| + | * Für das komplementäre Gaußsche Fehlerintegral können Sie folgende Näherungen verwenden: | ||
| + | :$${\rm Q }(1.5) \approx 0.0668\hspace{0.05cm}, \hspace{0.2cm}{\rm Q }(2.5) \approx 0.0062\hspace{0.05cm}, \hspace{0.2cm} | ||
| + | {\rm Q }(2.65) \approx 0.0040 | ||
| + | \hspace{0.05cm}.$$ | ||
| + | * Sie können Ihre Ergebnisse mit folgendem Berechnungstool kontrollieren: [[Nichtkohärentes On–Off–Keying]] | ||
| − | |||
===Fragebogen=== | ===Fragebogen=== | ||
| − | |||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Multiple-Choice | + | {Multiple-Choice |
|type="[]"} | |type="[]"} | ||
| − | + | + correct | |
| − | + | + | - false |
| − | |||
{Input-Box Frage | {Input-Box Frage | ||
|type="{}"} | |type="{}"} | ||
| − | $ | + | $xyz$ = { 5.4 3% } $ab$ |
| − | |||
| − | |||
| − | |||
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' |
| − | '''(2)''' | + | '''(2)''' |
| − | '''(3)''' | + | '''(3)''' |
| − | '''(4)''' | + | '''(4)''' |
| − | '''(5)''' | + | '''(5)''' |
| − | + | {{ML-Fuß}} | |
| − | |||
[[Category:Aufgaben zu Digitalsignalübertragung|^4.5 Inkohärente Demodulation^]] | [[Category:Aufgaben zu Digitalsignalübertragung|^4.5 Inkohärente Demodulation^]] | ||
Revision as of 20:33, 9 November 2017
Die Abbildung zeigt die beiden Dichtefunktionen, die sich bei einer nichtkohärenten Demodulation von On–Off–Keying ergeben. Dabei wird vorausgesetzt, dass die zwei OOK–Signalraumpunkte bei $\boldsymbol{s}_0 = C$ (Nachricht $m_0$) und bei $\boldsymbol{s}_1 = 0$ (Nachricht $m_1$) liegen.
Die Symbolfehlerwahrscheinlichkeit dieses Systems wird durch die folgende Gleichung beschrieben:
- $$p_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}({\cal{E}}) = $$
- $$\hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{ 2} \cdot \int_{0}^{G} p_{y|m} (\eta | m_0) \,{\rm d} \eta +$$
- $$ \hspace{-0.1cm} \ + \ \hspace{-0.1cm} {1}/{ 2} \cdot \int_{G}^{\infty} p_{y|m} (\eta | m_1) \,{\rm d} \eta \hspace{0.05cm}.$$
Mit der Streuung $\sigma_n = 1$, die im Folgenden vorausgesetzt wird, lautet die sich für $m = m_1$ ergebende Rayleighverteilung (blaue Kurve):
- $$p_{y|m} (\eta | m_1) = \eta \cdot {\rm e }^{-\eta^2/2} \hspace{0.05cm}.$$
Die Riceverteilung (rote Kurve) kann im vorliegenden Fall (wegen $C >> \sigma_n$) durch eine Gaußverteilung angenähert werden:
- $$p_{y|m} (\eta | m_0) = \frac{1}{\sqrt{2\pi}} \cdot {\rm e }^{-(\eta-C)^2/2} \hspace{0.05cm}.$$
Die optimale Entscheidergrenze $G_{\rm opt}$ ergibt sich aus dem Schnittpunkt von roter und blauer Kurve. Aus den beiden Skizzen erkennt man, dass $G_{\rm opt}$ von $C$ abhängt. Für die obere Grafik gilt $C = 4$, für die untere $C = 6$. Alle Größen sind normiert und es wird stets $\sigma_n = 1$ vorausgesetzt.
Hinweise:
- Die Aufgabe gehört zum Themengebiet des Kapitels Trägerfrequenzsysteme mit nichtkohärenter Demodulation.
- Für das komplementäre Gaußsche Fehlerintegral können Sie folgende Näherungen verwenden:
- $${\rm Q }(1.5) \approx 0.0668\hspace{0.05cm}, \hspace{0.2cm}{\rm Q }(2.5) \approx 0.0062\hspace{0.05cm}, \hspace{0.2cm} {\rm Q }(2.65) \approx 0.0040 \hspace{0.05cm}.$$
- Sie können Ihre Ergebnisse mit folgendem Berechnungstool kontrollieren: Nichtkohärentes On–Off–Keying
Fragebogen
Musterlösung