Aufgaben:Exercise 4.18: Non-Coherent FSK Demodulation

• Return to book

Nichtkohärente Demodulation

Wir betrachten Frequency Shift Keying (FSK) mit $M = 2$ ⇒ binäre Signalisierung. Die beiden Basisfunktionen im Tiefpassbereich sind in diesem Fall komplex und lauten

$$\xi_1(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{1/T} \cdot {\rm e}^{\hspace{0.05cm}+{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} \pi \hspace{0.03cm}\cdot \hspace{0.03cm} h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},$$

$$ \xi_2(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{1/T} \cdot {\rm e}^{\hspace{0.05cm}-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} \pi \hspace{0.03cm}\cdot \hspace{0.03cm} h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T \hspace{0.05cm}.$$

Für die zwei möglichen Signalformen im Tiefpassbereich gilt dann mit der mittleren Symbolenergie $E_{\rm S}$:

$$m_0 : s_{\rm TP,\hspace{0.05cm}0} = \sqrt{E_{\rm S}} \cdot \xi_1(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\boldsymbol{ s}_{\rm 0} = (\sqrt{E_{\rm S}}, 0)\hspace{0.05cm},$$

$$m_1 : s_{\rm TP,\hspace{0.05cm}1} = \sqrt{E_{\rm S}} \cdot \xi_2(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\boldsymbol{ s}_{\rm 1} = (0, \sqrt{E_{\rm S}})\hspace{0.05cm}.$$

Hierbei gibt $h$ den sog. Modulationsindex an. Dieser muss gewisse Kriterien erfüllen, damit sich auch nach der Demodulation orthogonale Signalformen ergeben. Diese Kriterien hängen allerdings davon ab, ob beim Empfänger ein kohärenter oder ein nichtkohärenter Demodulator verwendet wird.

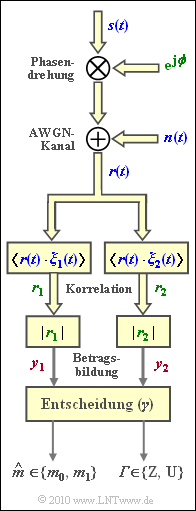
Die Grafik zeigt im unteren Bereich den nichtkohärenten Demodulator für binäres Frequency Shift Keying (FSK). Alle komplexen Signale sind blau beschriftet, komplexe Werte grün und reelle Werte rot.

Gegenüber dem im Theorieteil angegeben Entscheidungsprozess wird nun ein komplizierter Entscheider betrachtet, der außer dem Schätzwert noch ein Sicherheitsflag ${\it \Gamma} = \{„{\rm Z}”, \ „{\rm U}”\}$ ausgibt. „${\rm Z}$” und „${\rm U}$” stehen hierbei für eine zuverlässige bzw. eine unzuverlässige Entscheidung. Es gibt also vier Möglichkeiten der Entscheidung, gesteuert durch den Parameter $\gamma$:

$$\hat{m} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} m_0,\hspace{0.05cm}{\it \Gamma} = {\rm "Z"}, \hspace{0.2cm}{\rm falls} \hspace{0.15cm}y_1 > \gamma \cdot y_2\hspace{0.05cm},$$

$$\hat{m} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} m_0,\hspace{0.05cm}{\it \Gamma} = {\rm "U"}, \hspace{0.2cm}{\rm falls} \hspace{0.15cm}y_2 < y_1 < \gamma \cdot y_2\hspace{0.05cm},$$

$$\hat{m} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} m_1,\hspace{0.05cm}{\it \Gamma} = {\rm "Z"}, \hspace{0.2cm}{\rm falls} \hspace{0.15cm}y_2 > \gamma \cdot y_1\hspace{0.05cm},$$

$$\hat{m} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} m_1,\hspace{0.05cm}{\it \Gamma} = {\rm "U"}, \hspace{0.2cm}{\rm falls} \hspace{0.15cm}y_1 < y_2 < \gamma \cdot y_1\hspace{0.05cm}.$$

In den Fragen zur Aufgabe werden die beiden Werte $\gamma = 1$ und $\gamma = 2$ betrachtet.

Für die Wahrscheinlichkeit, dass sich der Entscheider fälschlicherweise für das Symbol $m_1$ entscheidet und zudem anzeigt, dass diese Entscheidung als zuverlässig zu betrachten ist (besonders verwerflich), gilt

$${\rm Pr}\{\hat{m} = m_1,\hspace{0.05cm}{\it \Gamma} = {\rm "Z"} \hspace{0.05cm}| \hspace{0.05cm}m_0 \} = \frac{1}{1 + \gamma^2} \cdot {\rm exp } \left [ - \frac{\gamma^2 \cdot E_{\rm S}}{(1+\gamma^2) \cdot N_{\rm 0}}\right ] \hspace{0.05cm}.$$

Hinweis:

• Die Aufgabe gehört zum Themengebiet des Kapitels Trägerfrequenzsysteme mit nichtkohärenter Demodulation.

Fragebogen

1

Welche Aussagen sind bei kohärenter Demodulation der FSK zutreffend?

	Orthogonalität ergibt sich, wenn $h$ ganzzahlig ist.
	Auch für $h = 0.5$ ergeben sich orthogonale Signalformen.
	Orthogonalität ist grundsätzlich nicht zu erreichen.
	Beim AWGN–Kanal gilt $r(t) = s(t) + n(t)$.

2

Welche Aussagen sind bei nichtkohärenter Demodulation der FSK zutreffend?

	Orthogonalität ergibt sich, wenn $h$ ganzzahlig ist.
	Auch für $h = 0.5$ ergeben sich orthogonale Signalformen.
	Orthogonalität ist grundsätzlich nicht zu erreichen.
	Beim AWGN–Kanal gilt $r(t) = s(t) + n(t)$.

3

Wie groß ist die Fehlerwahrscheinlichkeit, also die Wahrscheinlichkeit, dass der Schätzwert nicht mit der gesendeten Nachricht übereinstimmt? ($E_{\rm S}/N_0 = 10$).

$p_{\rm S} \ = \ { 3.37 3% } $\ \cdot 10^{\rm –3}$

4

Es sei $\gamma = 2$ und $E_{\rm S}/N_0 = 10$. Wie groß ist die Wahrscheinlichkeit, dass trotz Fehler das Sicherheitsflag eine zuverlässige Entscheidung signalisiert?

$\gamma = 2 \text{:} \hspace{0.4cm} {\rm Pr}({\it \Gamma} = \ {\rm „Z”, \ Fehler)} \ = \ { 6.7 3% } $\ \cdot 10^{\rm –5}$

5

Wie groß ist die (bedingte) Wahrscheinlichkeit, dass bei einem Fehler die Zusatzinformation „unzuverlässig” angezeigt wird? Es sei weiterhin $E_{\rm S}/N_0 = 10$.

$\gamma = 2 \text{:} \hspace{0.4cm} {\rm Pr}({\it \Gamma} = \ {\rm „U”, \ Fehler)} \ = \ { 6.7 3% } $\ \cdot 10^{\rm –5}$

Musterlösung

Solution

(1)  (2)  (3)  (4)  (5)