Difference between revisions of "Aufgaben:Exercise 2.6: Modified MS43 Code"
From LNTwww
| Line 7: | Line 7: | ||
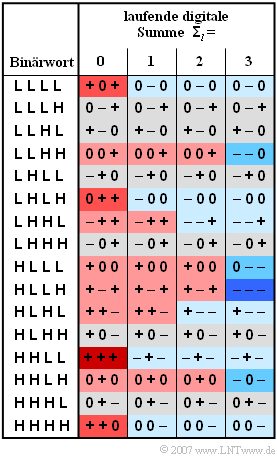
Bei der ISDN–Datenübertragung wird in Deutschland und Belgien auf der so genannten $\rm {U_{KO}}$–Schnittstelle, die den Übertragungsweg zwischen Vermittlungsstelle und Wohnung beschreibt, der MMS43–Code ''(Modified Monitored Sum 4B3T)'' eingesetzt. Hierbei handelt es sich um einen 4B3T–Code mit vier Codetabellen, die gemäß der laufenden digitalen Summe (nach $l$–Blöcken) | Bei der ISDN–Datenübertragung wird in Deutschland und Belgien auf der so genannten $\rm {U_{KO}}$–Schnittstelle, die den Übertragungsweg zwischen Vermittlungsstelle und Wohnung beschreibt, der MMS43–Code ''(Modified Monitored Sum 4B3T)'' eingesetzt. Hierbei handelt es sich um einen 4B3T–Code mit vier Codetabellen, die gemäß der laufenden digitalen Summe (nach $l$–Blöcken) | ||
:$${\it \Sigma}_l = \sum_{\nu = 1}^{3 \hspace{0.02cm}\cdot \hspace{0.05cm} l}\hspace{0.02cm} a_\nu$$ | :$${\it \Sigma}_l = \sum_{\nu = 1}^{3 \hspace{0.02cm}\cdot \hspace{0.05cm} l}\hspace{0.02cm} a_\nu$$ | ||
| − | zur Codierung herangezogen werden. Zur Initialisierung wird $\ | + | zur Codierung herangezogen werden. Zur Initialisierung wird $\Sigma_{0} = 0$ verwendet. |
| − | *Ändert sich die laufende digitale Summe nicht $(\ | + | *Ändert sich die laufende digitale Summe nicht $(\Sigma_{l+1} = \Sigma_{l})$, so ist ein Feld grau hinterlegt. |
| − | *Eine Zunahme $(\ | + | *Eine Zunahme $(\Sigma_{l+1} > \Sigma_{l})$ ist rot hinterlegt, eine Abnahme $(\Sigma_{l+1} < \Sigma_{l})$ blau. |
*Je intensiver die Farbgebung, um so größer ist die Änderung. | *Je intensiver die Farbgebung, um so größer ist die Änderung. | ||
| Line 22: | Line 22: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | |
| + | {Warum wird bei ISDN statt des redundanzfreien Binärcodes ein 4B3T–Code verwendet? | ||
|type="[]"} | |type="[]"} | ||
| − | - | + | - 4B3T ist immer besser als der redundanzfreie Binärcode. |
| − | + | + | + Das Sendesignal sollte wegen $H_{\rm K}(0) = 0$ gleichsignalfrei sein. |
| + | +Kleinere Schrittgeschwindigkeit erlaubt größere Kabellänge. | ||
| + | {Codieren Sie die binäre Folge „HHLL LHLL LHHL HLHL” (mit $\Sigma_{0} = 0$). Wie lautet der Amplitudenkoeffizient des dritten Ternärsymbols des vierten Blocks? | ||
| + | |type="{}"} | ||
| + | $a_{12} \ = \ $ { -1.03--0.97 } | ||
| − | { | + | |
| + | {Ermitteln Sie das Markovdiagramm für den Übergang von $\Sigma_{l}$ auf $\Sigma_{l+1}$. Welche Übergangswahrscheinlichkeiten ergeben sich? | ||
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $ {\Pr}(\Sigma_{l+1} = 0 | \Sigma_{l} = 0) \ = \ $ { 0.375 3% } |
| − | + | $ {\Pr}(\Sigma_{l+1} = 2 | \Sigma_{l} = 0) \ = \ $ { 0.1875 3% } | |
| + | $ {\Pr}(\Sigma_{l+1} = 0 | \Sigma_{l} = 2) \ = \ $ { 0 3% } | ||
| + | {Welche Eigenschaften folgen aus dem Markovdiagramm? | ||
| + | |type="[]"} | ||
| + | - Gleiche Wahrscheinlichkeiten: Pr($\Sigma_{l} = 0$) = ... = Pr($\Sigma_{l} = 3$). | ||
| + | + Es gilt Pr($\Sigma_{l} = 0$) = Pr($\Sigma_{l} = 3$) und Pr($\Sigma_{l} = 1$) = Pr($\Sigma_{l} =2$). | ||
| + | + Die Extremwerte ($0$ bzw. $3$) treten seltener auf als $1$ oder $2$. | ||
</quiz> | </quiz> | ||
Revision as of 11:02, 13 November 2017
Bei der ISDN–Datenübertragung wird in Deutschland und Belgien auf der so genannten $\rm {U_{KO}}$–Schnittstelle, die den Übertragungsweg zwischen Vermittlungsstelle und Wohnung beschreibt, der MMS43–Code (Modified Monitored Sum 4B3T) eingesetzt. Hierbei handelt es sich um einen 4B3T–Code mit vier Codetabellen, die gemäß der laufenden digitalen Summe (nach $l$–Blöcken)
- $${\it \Sigma}_l = \sum_{\nu = 1}^{3 \hspace{0.02cm}\cdot \hspace{0.05cm} l}\hspace{0.02cm} a_\nu$$
zur Codierung herangezogen werden. Zur Initialisierung wird $\Sigma_{0} = 0$ verwendet.
- Ändert sich die laufende digitale Summe nicht $(\Sigma_{l+1} = \Sigma_{l})$, so ist ein Feld grau hinterlegt.
- Eine Zunahme $(\Sigma_{l+1} > \Sigma_{l})$ ist rot hinterlegt, eine Abnahme $(\Sigma_{l+1} < \Sigma_{l})$ blau.
- Je intensiver die Farbgebung, um so größer ist die Änderung.
Hinweis:
- Diese Aufgabe bezieht sich auf Blockweise Codierung mit 4B3T-Codes. Die Binärsymbole werden in diesem Lerntutorial mit L („Low”) und H („High”) bezeichnet. Häufig findet man in der Literatur auch die Binärsymbole L und 0 (statt H). Manchmal entspricht aber auch L unserem H und 0 dem L.
- Damit eine solche Verwirrung vermieden wird und die „0” nicht in beiden Alphabeten (binär und ternär) – dazu noch mit unterschiedlicher Bedeutung – auftritt, wurde in LNTwww die zugegebenerweise etwas gewöhnungsbedürftige Nomenklatur verwendet. Wir sind uns durchaus bewusst, dass auch unsere Nomenklatur manche Leser verwirren wird.
- Sie können die Ergebnisse mit dem Interaktionsmodul Prinzip der 4B3T–Codierung überprüfen.
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)
(6)