Aufgaben:Exercise 5.2: Error Correlation Function

• Return to book

Gegebene Fehlerabstandswahrscheinlichkeiten und Fehlerkorrelationsfunktion

Zur Charakterisierung von digitalen Kanalmodellen verwendet man unter Anderem

• die Fehlerkorrelationsfunktion (FKF)

$$\varphi_{e}(k) = {\rm E}[e_{\nu} \cdot e_{\nu + k}]\hspace{0.05cm}, \hspace{0.2cm} k \ge 0\hspace{0.05cm},$$

• die Fehlerabstandswahrscheinlichkeiten

$${\rm Pr}( a =k) \hspace{0.05cm}, \hspace{0.2cm} k \ge 1\hspace{0.05cm}.$$

Hierbei bezeichnen

• $〈e_{\rm \nu}〉$ die Fehlerfolge mit $e_{\rm \nu} ∈ \{0, 1\}$, und
• $a$ den Fehlerabstand.

Zwei direkt aufeinanderfolgende Bitfehler werden somit durch den Fehlerabstand $a = 1$ gekennzeichnet.

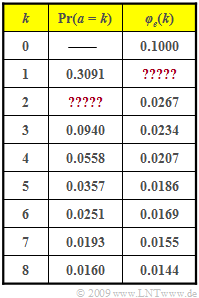
Die Tabelle zeigt beispielhafte Werte der Fehlerabstandswahrscheinlichkeiten ${\rm Pr}(a = k)$ sowie der Fehlerkorrelationsfunktion $\varphi_e(k)$. Einige Angaben fehlen in der Tabelle. Diese Werte sollen aus den gegebenen Werten berechnet werden.

Hinweise:

• Die Aufgabe behandel den Lehrstoff des Kapitels Beschreibungsgrößen digitaler Kanalmodelle.

Fragebogen

1

Welcher Wert ergibt sich für die mittlere Fehlerwahrscheinlichkeit?

$p_{\rm M} \ = \ $

2

Welcher Wert ergibt sich für den mittleren Fehlerabstand?

${\rm E}[a] \ = \ $

3

Berechnen Sie den FKF–Wert für $k = 1$.

$\varphi_r(k = 1) \ = \ $

4

Welche Näherung gilt für die Wahrscheinlichkeit des Fehlerabstands $a = 2$?

${\rm Pr}(a = 2) \ = \ $

Musterlösung

Solution

(1)  (2)  (3)  (4)  (5)