Aufgaben:Exercise 5.6: Error Correlation Duration

• Return to book

Fehlerkorrelationsfunktion beim GE–Modell

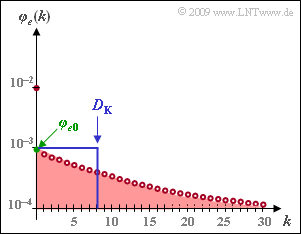
Die Grafik zeigt die Fehlerkorrelationsfunktion (FKF) des Gilbert–Elliott–Modells mit den Parametern

$$p_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.001, \hspace{0.2cm}p_{\rm B} = 0.1,$$

$$ {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.1, \hspace{0.2cm} {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) = 0.01\hspace{0.05cm}$$

in logarithmierter Darstellung.

Dieses Modell wird in der Aufgabe Aufgabe Z5.6 ausführlich behandelt. Insbesondere wird in dieser Aufgabe auch die Fehlerkorrelationsfunktion (FKF) berechnet. Mit den Hilfsgrößen

$$A \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (p_{\rm B}- p_{\rm M}) \cdot (p_{\rm M}- p_{\rm G})\hspace{0.05cm},$$

$$B\hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) + {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)$$

kann für diese geschrieben werden:

$$\varphi_{e}(k) = \left\{ \begin{array}{c} p_{\rm M} \\ p_{\rm M}^2 + A \cdot (1-B)^k \end{array} \right.\quad \begin{array}{*{1}c} f{\rm \ddot{u}r }\hspace{0.15cm}k = 0 \hspace{0.05cm}, \\ f{\rm \ddot{u}r }\hspace{0.15cm} k > 0 \hspace{0.05cm}.\\ \end{array}$$

Hierbei handelt es sich um einen Bündelfehlerkanal. Zur quantitativen Beschreibung der statistischen Bindungen verwendet man oft die Korrelationsdauer gemäß der folgenden Definition:

$$D_{\rm K} = \frac{1}{\varphi_{e0} - p_{\rm M}^2} \cdot \sum_{k = 1 }^{\infty}\hspace{0.1cm} [\varphi_{e}(k) - p_{\rm M}^2]\hspace{0.05cm}.$$

Der Bezugswert $\varphi_{e0}$ ergibt sich dabei durch Extrapolation der Fehlerkorrelationsfunktion in den Punkt $k = 0$. Ist wie hier der FKF–Verlauf analytisch gegeben, so kann man $\varphi_{e0}$ auch dadurch berechnen, dass man in die eigentlich nur für $k > 0$ gültige Gleichung den Wert $k = 0$ einsetzt.

Hinweis:

• Die Aufgabe gehört zum Themengebiet des Kapitels Bündelfehlerkanäle.

Fragebogen

1

Welcher FKF–Wert gilt exakt für $k = 0$?

$\varphi_e(k = 0) \ = \ $ $\ \cdot 10^{–2}$

2

Wie groß ist der aus der gegebenen FKF extrapolierte Wert für $k = 0$?

$\varphi_{e0} \ = \ $ $\ \cdot 10^{–3}$

3

Welches Ergebnis erhält man für die Fehlerkorrelationsdauer $D_{\rm K}$ mit den vorne definierte Größen $A$ und $B$?

	$D_{\rm K} = A \cdot B$,
	$D_{\rm K} = 1/A –B$,
	$D_{\rm K} = 1/N –1$.

4

Welche Korrelationsdauer ergibt sich beim vorliegenden GE–Modell?

$D_{\rm K} \ = \ $

5

Welche Aussagen gelten bezüglich der Korrelationsdauer $D_{\rm K}$ des GE–Modells? Beachten Sie für Ihre Antwort die logarithmische Ordinate.

	$D_{\rm K}$ bleibt gleich, wenn man ${\rm Pr}({\rm B|G})$ und ${\rm Pr(G|B)}$ vertauscht.
	$D_{\rm K}$ hängt nur von der Summe ${\rm Pr(G|B)} + Pr(B|G)}$ ab.
	Die rote Fläche in der Grafik ist gleich der blauen Rechteckfläche.

Musterlösung

Solution

(1)  (2)  (3)  (4)  (5)