Difference between revisions of "Aufgaben:Exercise 5.6Z: Gilbert-Elliott Model"
From LNTwww
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Digitalsignalübertragung/Bündelfehlerkanäle}} Datei:P_ID1842__Dig_A_5_6.png|right|frame|Fehlerkorrelationsfunktion beim GE–Mod…“) |
|||
| Line 2: | Line 2: | ||
{{quiz-Header|Buchseite=Digitalsignalübertragung/Bündelfehlerkanäle}} | {{quiz-Header|Buchseite=Digitalsignalübertragung/Bündelfehlerkanäle}} | ||
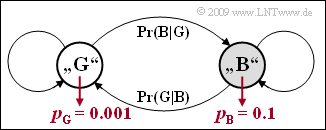
| − | [[File: | + | [[File:P_ID1843__Dig_Z_5_6.png|right|frame|GE–Modell]] |
| + | Wir betrachten das <i>Bündelfehler–Kanalmodell</i> nach E.N. Gilbert und E.O. Elliott (siehe Skizze). Für die Übergangswahrscheinlichkeiten soll dabei gelten: | ||
| + | :$${\rm Pr}(\rm | ||
| + | G\hspace{0.05cm}|\hspace{0.05cm} B)= 0.1, \hspace{0.2cm} {\rm | ||
| + | Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) = 0.01\hspace{0.05cm}.$$ | ||
| + | |||
| + | Die Fehlerwahrscheinlichkeit im Zustand „GOOD” betrage $p_{\rm G} = 0.1\%$ und für die im Zustand „BAD” gelte $p_{\rm B} = 10\%$. Im Verlaufe dieser Aufgabe sollen weitere Kenngrößen ermittelt werden: | ||
| + | * die mittlere Fehlerwahrscheinlichkeit $p_{\rm M}$, | ||
| + | * die Zustandswahrscheinlichkeiten $w_{\rm G} = \rm Pr(Z = G)$ und $w = \rm Pr(Z = B)$, | ||
| + | * die Werte der Korrelationsfunktion, die für $k > 0$ analytisch wie folgt gegeben ist: | ||
| + | :$$\varphi_{e}(k) = p_{\rm M}^2 + (p_{\rm B} - | ||
| + | p_{\rm M}) \cdot (p_{\rm M} - p_{\rm G}) \cdot | ||
| + | [1 - {\rm Pr}(\rm | ||
| + | B\hspace{0.05cm}|\hspace{0.05cm} G )- {\rm Pr}(\rm | ||
| + | G\hspace{0.05cm}|\hspace{0.05cm} B )]^{\it k} \hspace{0.05cm}.$$ | ||
| + | |||
| + | ''Hinweis:'' | ||
| + | * Die Aufgabe bezieht sich auf das Kapitel [[Digitalsignal%C3%BCbertragung/B%C3%BCndelfehlerkan%C3%A4le| Bündelfehlerkanal]] des vorliegenden Buches sowie auf das Kapitel [[Stochastische_Signaltheorie/Markovketten| Markovketten]] im Buch „Stochastische Signaltheorie”. | ||
Revision as of 12:08, 14 November 2017
Wir betrachten das Bündelfehler–Kanalmodell nach E.N. Gilbert und E.O. Elliott (siehe Skizze). Für die Übergangswahrscheinlichkeiten soll dabei gelten:
- $${\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)= 0.1, \hspace{0.2cm} {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) = 0.01\hspace{0.05cm}.$$
Die Fehlerwahrscheinlichkeit im Zustand „GOOD” betrage $p_{\rm G} = 0.1\%$ und für die im Zustand „BAD” gelte $p_{\rm B} = 10\%$. Im Verlaufe dieser Aufgabe sollen weitere Kenngrößen ermittelt werden:
- die mittlere Fehlerwahrscheinlichkeit $p_{\rm M}$,
- die Zustandswahrscheinlichkeiten $w_{\rm G} = \rm Pr(Z = G)$ und $w = \rm Pr(Z = B)$,
- die Werte der Korrelationsfunktion, die für $k > 0$ analytisch wie folgt gegeben ist:
- $$\varphi_{e}(k) = p_{\rm M}^2 + (p_{\rm B} - p_{\rm M}) \cdot (p_{\rm M} - p_{\rm G}) \cdot [1 - {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )- {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B )]^{\it k} \hspace{0.05cm}.$$
Hinweis:
- Die Aufgabe bezieht sich auf das Kapitel Bündelfehlerkanal des vorliegenden Buches sowie auf das Kapitel Markovketten im Buch „Stochastische Signaltheorie”.
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)