Difference between revisions of "Aufgaben:Exercise 5.7Z: McCullough Model once more"
m (Hussain verschob die Seite Zusatzaufgaben:5.7 Nochmals MC-Modell nach 5.7Z Nochmals MC-Modell) |
|||
| Line 2: | Line 2: | ||
{{quiz-Header|Buchseite=Digitalsignalübertragung/Bündelfehlerkanäle}} | {{quiz-Header|Buchseite=Digitalsignalübertragung/Bündelfehlerkanäle}} | ||
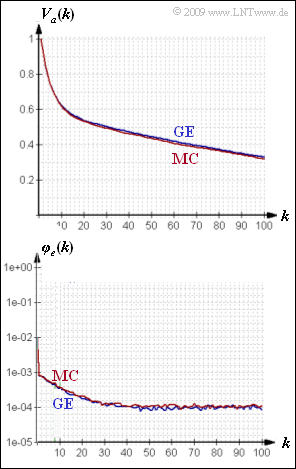
| − | [[File: | + | [[File:P_ID1845__Dig_Z_5_7.png|right|frame|Fehlerabstandsverteilung und -korrelationsfunktion von GE–Modell und äquivalentem MC-Modell]] |
| + | Wir betrachten wie auch in den Aufgaben A5.6, Z5.6 und A5.7 das Bündelfehler–Kanalmodell nach Gilbert und Elliott (GE–Modell) mit den Kenngrößen | ||
| + | :$$p_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.001, | ||
| + | \hspace{0.2cm}p_{\rm B} = 0.1,$$ | ||
| + | :$$ p(\rm | ||
| + | G\hspace{0.05cm}|\hspace{0.05cm} B)\hspace{-0.1cm} \ = \ | ||
| + | \hspace{-0.1cm} 0.1, \hspace{0.2cm} p(\rm | ||
| + | B\hspace{0.05cm}|\hspace{0.05cm} G) = 0.01\hspace{0.05cm}.$$ | ||
| + | |||
| + | Aus diesen vier Wahrscheinlichkeiten lassen sich die entsprechenden Kenngrößen des Kanalmodells nach McCullough (MC–Modell) so ermitteln, dass beide Modelle die genau gleichen statistischen Eigenschaften besitzen, nämlich | ||
| + | * exakt gleiche Fehlerabstandsverteilung $V_a(k)$, | ||
| + | * exakt gleiche Fehlerkorrelationsfunktion $\varphi_e(k)$. | ||
| + | |||
| + | |||
| + | Die Wahrscheinlichkeiten des MC–Modells wurden in der [[Aufgaben:5.7_MC-_aus_GE-Parameter| Aufgabe A5.7]] wie folgt ermittelt (Bezeichnungen entsprechend der Grafik zur Aufgabe A5.7, alle mit „$q$” anstelle von „$p$”): | ||
| + | :$$q_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.0061, | ||
| + | \hspace{0.2cm}q_{\rm B} = 0.1949,$$ | ||
| + | :$$ q(\rm | ||
| + | G\hspace{0.05cm}|\hspace{0.05cm} B)\hspace{-0.1cm} \ = \ | ||
| + | \hspace{-0.1cm} 0.5528, \hspace{0.2cm} q(\rm | ||
| + | B\hspace{0.05cm}|\hspace{0.05cm} G) = 0.3724\hspace{0.05cm}.$$ | ||
| + | |||
| + | Die obere Grafik zeigt die aus $N = 10^6$ Folgenelementen simulativ ermittelten Funktionen $V_a(k)$ und $\varphi_e(k)$ für das GE– und das MC–Modell. Hier ergeben sich noch leichte Abweichungen. Im Grenzfall für $N → ∞$ stimmen dagegen Fehlerkorrelationsfunktion und Fehlerabstandsverteilung beider Modelle exakt überein. | ||
| + | |||
| + | In dieser Aufgabe sollen nun wichtige Beschreibungsgrößen wie Zustandswahrscheinlichkeiten, mittlere Fehlerwahrscheinlichkeiten und Korrelationsdauer direkt aus den $q$–Parametern des MC–Modells ermittelt werden. | ||
| + | |||
| + | ''Hinweis:'' | ||
| + | * Die Aufgabe gehört zum Themengebiet von [[Digitalsignal%C3%BCbertragung/B%C3%BCndelfehlerkan%C3%A4le| Kapitel 5.3]]. | ||
| + | * Aus den oben genannten Aufgaben können folgende Ergebnisse weiterverwendet werden: | ||
| + | ** Die Zustandswahrscheinlichkeiten des GE–Modells sind | ||
| + | :$$w_{\rm G} = \frac{p(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)}{p(\rm | ||
| + | G\hspace{0.05cm}|\hspace{0.05cm} B) + p(\rm | ||
| + | B\hspace{0.05cm}|\hspace{0.05cm} G)} | ||
| + | \hspace{0.05cm},\hspace{0.2cm} w_{\rm B} = 1 - w_{\rm G | ||
| + | }\hspace{0.05cm}.$$ | ||
| + | ** Die mittlere Fehlerwahrscheinlichkeit des GE–Modells beträgt | ||
| + | :$$p_{\rm M} = w_{\rm G} \cdot p_{\rm G} + w_{\rm B} \cdot p_{\rm B} | ||
| + | = \varphi_{e}(k = 0 )\hspace{0.05cm}.$$ | ||
| + | ** Die Korrelationsdauer des GE–Modells berechnet sich zu | ||
| + | :$$D_{\rm K} =\frac{1}{{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} | ||
| + | B ) + {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )}-1 | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
Revision as of 18:02, 14 November 2017
Wir betrachten wie auch in den Aufgaben A5.6, Z5.6 und A5.7 das Bündelfehler–Kanalmodell nach Gilbert und Elliott (GE–Modell) mit den Kenngrößen
- $$p_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.001, \hspace{0.2cm}p_{\rm B} = 0.1,$$
- $$ p(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.1, \hspace{0.2cm} p(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) = 0.01\hspace{0.05cm}.$$
Aus diesen vier Wahrscheinlichkeiten lassen sich die entsprechenden Kenngrößen des Kanalmodells nach McCullough (MC–Modell) so ermitteln, dass beide Modelle die genau gleichen statistischen Eigenschaften besitzen, nämlich
- exakt gleiche Fehlerabstandsverteilung $V_a(k)$,
- exakt gleiche Fehlerkorrelationsfunktion $\varphi_e(k)$.
Die Wahrscheinlichkeiten des MC–Modells wurden in der Aufgabe A5.7 wie folgt ermittelt (Bezeichnungen entsprechend der Grafik zur Aufgabe A5.7, alle mit „$q$” anstelle von „$p$”):
- $$q_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.0061, \hspace{0.2cm}q_{\rm B} = 0.1949,$$
- $$ q(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.5528, \hspace{0.2cm} q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) = 0.3724\hspace{0.05cm}.$$
Die obere Grafik zeigt die aus $N = 10^6$ Folgenelementen simulativ ermittelten Funktionen $V_a(k)$ und $\varphi_e(k)$ für das GE– und das MC–Modell. Hier ergeben sich noch leichte Abweichungen. Im Grenzfall für $N → ∞$ stimmen dagegen Fehlerkorrelationsfunktion und Fehlerabstandsverteilung beider Modelle exakt überein.
In dieser Aufgabe sollen nun wichtige Beschreibungsgrößen wie Zustandswahrscheinlichkeiten, mittlere Fehlerwahrscheinlichkeiten und Korrelationsdauer direkt aus den $q$–Parametern des MC–Modells ermittelt werden.
Hinweis:
- Die Aufgabe gehört zum Themengebiet von Kapitel 5.3.
- Aus den oben genannten Aufgaben können folgende Ergebnisse weiterverwendet werden:
- Die Zustandswahrscheinlichkeiten des GE–Modells sind
- $$w_{\rm G} = \frac{p(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)}{p(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) + p(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)} \hspace{0.05cm},\hspace{0.2cm} w_{\rm B} = 1 - w_{\rm G }\hspace{0.05cm}.$$
- Die mittlere Fehlerwahrscheinlichkeit des GE–Modells beträgt
- $$p_{\rm M} = w_{\rm G} \cdot p_{\rm G} + w_{\rm B} \cdot p_{\rm B} = \varphi_{e}(k = 0 )\hspace{0.05cm}.$$
- Die Korrelationsdauer des GE–Modells berechnet sich zu
- $$D_{\rm K} =\frac{1}{{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) + {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )}-1 \hspace{0.05cm}.$$
Fragebogen
Musterlösung