| Line 111: | Line 111: | ||
::<math>p_2(x) = x^2 + 1 \hspace{0.06cm} = (x+1) \cdot (x+1)\hspace{0.05cm},</math> | ::<math>p_2(x) = x^2 + 1 \hspace{0.06cm} = (x+1) \cdot (x+1)\hspace{0.05cm},</math> | ||
::<math>p_3(x) =x^2 \hspace{0.76cm} = x \cdot x \hspace{0.05cm},</math> | ::<math>p_3(x) =x^2 \hspace{0.76cm} = x \cdot x \hspace{0.05cm},</math> | ||
| − | ::<math>p_4(x) = x^2 + x = (x+1) \cdot x </math> | + | ::<math>p_4(x) = x^2 + x = (x+1) \cdot x\hspace{0.05cm}, </math> |
lassen sich faktorisieren und ergeben keinen Erweiterungskörper. | lassen sich faktorisieren und ergeben keinen Erweiterungskörper. | ||
| − | *Man nennt die Polynome $p_2(x)$, $p_3(x)$ und $p_4(x)$ ''reduzibel''.}}<br> | + | *Man nennt die Polynome $p_2(x)$, $p_3(x)$ und $p_4(x)$ ''reduzibel''. Der Schluss liegt nahe, dass für einen Erweiterungskörper nur ''irreduzible Polynome'' wie $p_1(x)$ geeignet sind.}}<br> |
| − | == | + | == Interpretation des neuen Elementes $\alpha$ == |
<br> | <br> | ||
| − | Wir betrachten weiterhin den Körper GF(2 | + | Wir betrachten weiterhin den Körper ${\rm GF}(2^2) = \{0, 1, \alpha, 1 + \alpha\}$ entsprechend den beiden folgenden Operationstabellen, basierend auf der Nebenbedingung $p(\alpha)= \alpha^2 + \alpha + 1 = 0$ (irreduzibles Ploynom): |
| − | + | :$$ \begin{array}{c} | |
| − | + | {\rm modulo}\hspace{0.15cm} p(\alpha)= \alpha^2 + \alpha + 1\\ | |
| − | + | \end{array}\hspace{0.25cm} \Rightarrow\hspace{0.25cm} | |
| − | {| | + | \left[ \begin{array}{c|cccccc} + & 0 & 1 & \alpha & 1\!+\!\alpha \\ \hline |
| − | + | 0 & 0 & 1 & \alpha & 1\!+\!\alpha \\ | |
| − | + | 1 & 1 & 0 & 1\!+\!\alpha & \alpha \\ | |
| − | + | \alpha & \alpha & 1\!+\!\alpha & 0 & 1 \\ | |
| − | + | 1\!+\!\alpha & 1\!+\!\alpha & \alpha & 1 & 0 | |
| − | + | \end{array} \right] \hspace{-0.1cm} ,\hspace{0.5cm} | |
| − | ! | + | \left[ \begin{array}{c|cccccc} \cdot & 0 & 1 & \alpha & 1\!+\!\alpha \\ |
| − | + | \hline | |
| − | + | 0 & 0 & 0 & 0 & 0 \\ | |
| − | + | 1 & 0 & 1 & \alpha & 1\!+\!\alpha \\ | |
| − | + | \alpha & 0 & \alpha & 1\!+\!\alpha & 1 \\ | |
| − | + | 1\!+\!\alpha & 0 & 1\!+\!\alpha & 1 & \alpha | |
| − | + | \end{array} \right] .$$ | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ! | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | { | ||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ! | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ! | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Welche Bedeutung hat aber nun das neue Element $\alpha$? | |
| + | [[File:P ID2552 KC T 2 2 S1 v2.png|right|frame|Übergang von GF(2) zu GF(2<sup>2</sup>) |class=fit]] | ||
| + | *Das Polynom $p(\alpha)= \alpha^2 + \alpha + 1 $ hat keine Nullstelle in ${\rm GF}(2) = \{0, 1\}$. Das bedeutet weiter, dass $\alpha$ weder $0$ noch $1$ sein kann.<br> | ||
| − | * | + | *Wäre $\alpha= 0$ bzw. $\alpha= 1$, so wären zudem zwei der vier Mengenelemente $\{0, 1, \alpha, 1 + \alpha\}$jeweils identisch. Entweder „$0$” und „$\alpha$” sowie „$1$” und „$1+\alpha$” oder „$1$” und „$\alpha$” sowie „$0$” und „$1+\alpha$”. |
| − | + | *Vielmehr erhält der eindimensionale Körper ${\rm GF}(2)$ durch die Einführung des Elementes $\alpha$ eine zweite Dimension. Er wird also zum Galoisfeld ${\rm GF}(2^2)$ erweitert, wie die nebenstehende Grafik zeigt. | |
| − | *Das Element | + | *Das Element $\alpha$ hat ähnliche Bedeutung wie die imaginäre Einheit ${\rm j}$, durch die man die Menge der reellen Zahlen unter der Nebenbedingung ${\rm j}^2 + 1 = 0$ zur Menge der komplexen Zahlen erweitert. |
| + | <br clear=all> | ||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Übliche Darstellung des binären Erweiterungskörpers {\rm GF}(2^2):}$ | ||
| + | |||
| + | Aufgrund der Identität $\alpha^2 = 1 + \alpha$, die aus der Nebenbedingung $p(\alpha) = 0$ folgt, kann man in gleicher Weise ${\rm GF}(2^2) = \{0, 1, \alpha, \alpha^2\}$schreiben, wobei nun folgende Operationstabellen gelten: | ||
| − | + | :$$ \begin{array}{c} | |
| − | + | {\rm modulo}\hspace{0.15cm} p(\alpha)= \alpha^2 + \alpha + 1\\ | |
| − | + | \end{array}\hspace{0.25cm} \Rightarrow\hspace{0.25cm} | |
| − | { | + | \left[ \begin{array}{c\vertcccccc} + & 0 & 1 & \alpha & \alpha^2 \\ \hline |
| − | + | 0 & 0 & 1 & \alpha & \alpha^2 \\ | |
| − | + | 1 & 1 & 0 & \alpha^2 & \alpha \\ | |
| − | + | \alpha & \alpha & \alpha^2 & 0 & 1 \\ | |
| − | + | \alpha^2 & \alpha^2 & \alpha & 1 & 0 | |
| − | + | \end{array} \right] \hspace{-0.1cm} ,\hspace{0.5cm} | |
| − | + | \left[ \begin{array}{c\vertcccccc} \cdot & 0 & 1 & \alpha & \alpha^2 \\ | |
| − | + | \hline | |
| − | + | 0 & 0 & 0 & 0 & 0 \\ | |
| − | + | 1 & 0 & 1 & \alpha & \alpha^2 \\ | |
| − | + | \alpha & 0 & \alpha &\alpha^2 & 1 \\ | |
| − | + | \alpha^2 & 0 & \alpha^2 & 1 & \alpha | |
| − | + | \end{array} \right] .$$}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | { | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == Polynome über einem endlichen Körper | + | |
| + | |||
| + | == Polynome über einem endlichen Körper == | ||
<br> | <br> | ||
Ein Polynom in einem endlichen Körper GF(<i>P</i>), wobei <i>P</i> eine Primzahl angibt, hat folgende Form: | Ein Polynom in einem endlichen Körper GF(<i>P</i>), wobei <i>P</i> eine Primzahl angibt, hat folgende Form: | ||
| Line 347: | Line 243: | ||
{{Beispiel}}''':''' Es gelte <i>b</i>(<i>x</i>) = <i>x</i><sup>3</sup> + <i>x</i> + 1, <i>p</i><sub>1</sub>(<i>x</i>) = <i>x</i><sup>2</sup> + <i>x</i> + 1 und <i>p</i><sub>2</sub>(<i>x</i>) = <i>x</i><sup>2</sup> + 1. Die Grafik verdeutlicht links die Modulo–2–Multiplikation <i>a</i>(<i>x</i>) = <i>b</i>(<i>x</i>) · <i>p</i><sub>1</sub>(<i>x</i>). Das Ergebnis ist <i>a</i>(<i>x</i>) = <i>x</i><sup>5</sup> + <i>x</i><sup>4</sup> + 1.<br> | {{Beispiel}}''':''' Es gelte <i>b</i>(<i>x</i>) = <i>x</i><sup>3</sup> + <i>x</i> + 1, <i>p</i><sub>1</sub>(<i>x</i>) = <i>x</i><sup>2</sup> + <i>x</i> + 1 und <i>p</i><sub>2</sub>(<i>x</i>) = <i>x</i><sup>2</sup> + 1. Die Grafik verdeutlicht links die Modulo–2–Multiplikation <i>a</i>(<i>x</i>) = <i>b</i>(<i>x</i>) · <i>p</i><sub>1</sub>(<i>x</i>). Das Ergebnis ist <i>a</i>(<i>x</i>) = <i>x</i><sup>5</sup> + <i>x</i><sup>4</sup> + 1.<br> | ||
| − | [[File:P ID2538 KC T 2 2 S2 v2.png|Beispiel für Polynom–Multiplikation und –Division|class=fit]] | + | [[File:P ID2538 KC T 2 2 S2 v2.png|center|frame|Beispiel für Polynom–Multiplikation und –Division|class=fit]] |
Im rechten Teil der obigen Grafik ist die Modulo–2–Division <i>q</i>(<i>x</i>) = <i>a</i>(<i>x</i>)/<i>p</i><sub>2</sub>(<i>x</i>) mit dem Ergebnis <i>q</i>(<i>x</i>) = <i>x</i><sup>3</sup> + <i>x</i><sup>2</sup> + <i>x</i> + 1 dargestellt. Es verbleibt der Rest <i>r</i>(<i>x</i>) = <i>x</i>. Allein nach dieser Rechnung könnte <i>a</i>(<i>x</i>) = <i>x</i><sup>5</sup> + <i>x</i><sup>4</sup> + 1 durchaus ein irreduzibles Polynom sein.<br> | Im rechten Teil der obigen Grafik ist die Modulo–2–Division <i>q</i>(<i>x</i>) = <i>a</i>(<i>x</i>)/<i>p</i><sub>2</sub>(<i>x</i>) mit dem Ergebnis <i>q</i>(<i>x</i>) = <i>x</i><sup>3</sup> + <i>x</i><sup>2</sup> + <i>x</i> + 1 dargestellt. Es verbleibt der Rest <i>r</i>(<i>x</i>) = <i>x</i>. Allein nach dieser Rechnung könnte <i>a</i>(<i>x</i>) = <i>x</i><sup>5</sup> + <i>x</i><sup>4</sup> + 1 durchaus ein irreduzibles Polynom sein.<br> | ||
| Line 379: | Line 275: | ||
Ein Galoisfeld GF(<i>q</i>) mit <i>q</i> Elementen lässt sich also immer dann angeben, wenn die Elementenanzahl in der Form <i>q</i> = <i>P<sup>m</sup></i> geschrieben werden kann (<i>P</i> kennzeichnet eine Primzahl, <i>m</i> sei ganzzahlig).<br> | Ein Galoisfeld GF(<i>q</i>) mit <i>q</i> Elementen lässt sich also immer dann angeben, wenn die Elementenanzahl in der Form <i>q</i> = <i>P<sup>m</sup></i> geschrieben werden kann (<i>P</i> kennzeichnet eine Primzahl, <i>m</i> sei ganzzahlig).<br> | ||
| − | [[File:P ID2500 KC T 2 2 S3 v2.png|Mögliche Galoisfelder GF(<i>q</i>), <i>q</i> ≤ 64 |class=fit]]<br> | + | [[File:P ID2500 KC T 2 2 S3 v2.png|center|frame|Mögliche Galoisfelder GF(<i>q</i>), <i>q</i> ≤ 64 |class=fit]]<br> |
Die Grafik zeigt, für welche <i>q</i>–Werte sich jeweils ein Galoisfeld konstruieren lässt. Für die schraffiert eingezeichneten <i>q</i>–Werte ist kein endlicher Körper angebbar. Weiter ist anzumerken: | Die Grafik zeigt, für welche <i>q</i>–Werte sich jeweils ein Galoisfeld konstruieren lässt. Für die schraffiert eingezeichneten <i>q</i>–Werte ist kein endlicher Körper angebbar. Weiter ist anzumerken: | ||
| Line 396: | Line 292: | ||
Elementen. In der Tabelle sind für 2 ≤ <i>m</i> ≤ 6 alle irreduziblen Polynome des Galoisfeldes GF(2) angegeben. Die Polynome in Spalte 2 und 3 sind nicht nur irreduzibel, sondern auch primitiv.<br> | Elementen. In der Tabelle sind für 2 ≤ <i>m</i> ≤ 6 alle irreduziblen Polynome des Galoisfeldes GF(2) angegeben. Die Polynome in Spalte 2 und 3 sind nicht nur irreduzibel, sondern auch primitiv.<br> | ||
| − | [[File:P ID2501 KC T 2 2 S4 v4.png|Irreduzible und primitive Polynome|class=fit]]<br> | + | [[File:P ID2501 KC T 2 2 S4 v4.png|center|frame|Irreduzible und primitive Polynome|class=fit]]<br> |
Bevor wir uns der Definition eines primitiven Polynoms zuwenden, sollen zunächst die Besonderheiten primitiver Elemente am Beispiel von | Bevor wir uns der Definition eines primitiven Polynoms zuwenden, sollen zunächst die Besonderheiten primitiver Elemente am Beispiel von | ||
| Line 479: | Line 375: | ||
Die Grafik zeigt den endlichen Erweiterungskörper GF(2<sup>3</sup>) in einer 3D–Darstellung, wobei die Achsen mit <i>α</i><sup>0</sup> = 1, <i>α</i><sup>1</sup> und <i>α</i><sup>2</sup> bezeichnet sind. Die 2<sup>3</sup> = 8 Punkte im dreidimensionalen Raum sind mit den Koeffizientenvektoren beschriftet, wobei die Zuordnung der einzelnen Koeffizienten <i>k</i><sub>2</sub>, <i>k</i><sub>1</sub>, <i>k</i><sub>0</sub> zu den Achsen farblich deutlich gemacht ist. <br><br><br><br><br> | Die Grafik zeigt den endlichen Erweiterungskörper GF(2<sup>3</sup>) in einer 3D–Darstellung, wobei die Achsen mit <i>α</i><sup>0</sup> = 1, <i>α</i><sup>1</sup> und <i>α</i><sup>2</sup> bezeichnet sind. Die 2<sup>3</sup> = 8 Punkte im dreidimensionalen Raum sind mit den Koeffizientenvektoren beschriftet, wobei die Zuordnung der einzelnen Koeffizienten <i>k</i><sub>2</sub>, <i>k</i><sub>1</sub>, <i>k</i><sub>0</sub> zu den Achsen farblich deutlich gemacht ist. <br><br><br><br><br> | ||
| − | == Aufgaben == | + | == Aufgaben zum Kapitel== |
<br> | <br> | ||
[[Aufgaben:2.3 Reduzible und irreduzible Polynome|A2.3 Reduzible und irreduzible Polynome]] | [[Aufgaben:2.3 Reduzible und irreduzible Polynome|A2.3 Reduzible und irreduzible Polynome]] | ||
Revision as of 15:19, 21 November 2017
Contents
- 1 GF(22) – Beispiel eines Erweiterungskörpers
- 2 Reduzible und irreduzible Polynome
- 3 Interpretation des neuen Elementes $\alpha$
- 4 Polynome über einem endlichen Körper
- 5 Polynome über einem endlichen Körper (2)
- 6 Verallgemeinerte Definition eines Erweiterungskörpers
- 7 Binäre Erweiterungskörper (1)
- 8 Primitive Polynome
- 9 Binäre Erweiterungskörper (3)
- 10 Aufgaben zum Kapitel
GF(22) – Beispiel eines Erweiterungskörpers
Im Abschnitt Beispiel 2 im Kapitel „Einige_Grundlagen der Algebra” wurde bereits gezeigt, dass die endliche Zahlenmenge $\{0, 1, 2, 3\}$ ⇒ $q = 4$ nicht die Eigenschaften eines Galoisfeldes $\rm GF(4)$ erfüllt. Vielmehr ergeben sich für die Addition modulo 4 und die Multiplikation modulo 4 folgende Tabellen:
- $$ \begin{array}{c} {\rm modulo}\hspace{0.15cm}{\it q} = 4\\ \end{array}\hspace{0.25cm} \Rightarrow\hspace{0.25cm}\text{Addition: } \left[ \begin{array}{c|cccccc} + & 0 & 1 &2 & 3 \\ \hline 0 & 0 & 1 &2 & 3 \\ 1 & 1 & 2 &3 & 0 \\ 2 & 2 & 3 &0 & 1 \\ 3 & 3 & 0 &1 & 2 \end{array} \right] \hspace{-0.1cm} ,\hspace{0.25cm}\text{Multiplikation: } \left[ \begin{array}{c|cccccc} \cdot & 0 & 1 &2 & 3 \\ \hline 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 2 & 3 \\ 2 & 0 & 2 & 0 & 2 \\ 3 & 0 & 3 & 2 & 1 \\ \end{array} \right] . $$
Für $z_i = 2$ gibt es keine multiplikative Inverse ${\rm Inv_M}(z_i)$. Dies erkennt man daran, dass kein einziges Element $z_j ∈ \{0, 1, 2, 3\}$ die Bedingung $2 · z_j = 1$ erfüllt. Geht man dagegen vom binären Galoisfeld ${\rm GF}(2) = \{0, 1\}$ aus und erweitert dieses entsprechend der Gleichung
- \[{\rm GF}(2^2)= \big\{k_0+k_1\cdot \alpha \ \big | \ k_0, k_1\in{\rm GF}(2) = \{ 0, 1\} \big \}\hspace{0.05cm}, \]
so ergibt sich die ebenfalls endliche Menge $\{0, 1, \alpha, 1 + \alpha\}$ ⇒ die Ordnung ist weiterhin $q=4$. Führt man die Rechenoperationen modulo $p(\alpha) = \alpha^2 + \alpha + 1$ durch, so erhält man das folgende Ergebnis:
- $$ \begin{array}{c} {\rm modulo}\hspace{0.15cm}{\it p}(\alpha)= \alpha^2 + \alpha + 1\\ \end{array}\hspace{0.25cm} \Rightarrow\hspace{0.25cm} \left[ \begin{array}{c|cccccc} + & 0 & 1 & \alpha & 1\!+\!\alpha \\ \hline 0 & 0 & 1 & \alpha & 1\!+\!\alpha \\ 1 & 1 & 0 & 1\!+\!\alpha & \alpha \\ \alpha & \alpha & 1\!+\!\alpha & 0 & 1 \\ 1\!+\!\alpha & 1\!+\!\alpha & \alpha & 1 & 0 \end{array} \right] \hspace{-0.1cm} ,\hspace{0.5cm} \left[ \begin{array}{c|cccccc} \cdot & 0 & 1 & \alpha & 1\!+\!\alpha \\ \hline 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & \alpha & 1\!+\!\alpha \\ \alpha & 0 & \alpha & 1\!+\!\alpha & 1 \\ 1\!+\!\alpha & 0 & 1\!+\!\alpha & 1 & \alpha \end{array} \right] .$$
Hierzu ist anzumerken:
- Die neutralen Elemente der Addition bzw. Multiplikation sind weiterhin $N_{\rm A} = 0$ und $N_{\rm M} = 1$ .
- Da bei Modulo–Ausführung kein Unterschied zwischen Addition und Subtraktion besteht, ist $\alpha + \alpha = \alpha - \alpha = 0$. Für alle zi gilt somit: Die additive Inverse von $z_i$ ist das Element $z_i$ selbst.
- Die Einträge in der Multiplikationstabelle ergeben sich nach folgenden Berechnungen:
- \[\big [ \alpha \cdot (1+\alpha) \big ] \hspace{0.15cm}{\rm mod} \hspace{0.15cm} p(\alpha) = (\alpha^2 + \alpha) \hspace{0.15cm}{\rm mod} \hspace{0.15cm} (\alpha^2 + \alpha + 1)= 1\hspace{0.05cm},\]
- \[\big [ \alpha \cdot \alpha \big ] \hspace{0.15cm}{\rm mod} \hspace{0.15cm} p(\alpha) = (\alpha^2 ) \hspace{0.15cm}{\rm mod} \hspace{0.15cm} (\alpha^2 + \alpha + 1)= 1+\alpha\hspace{0.05cm},\]
- \[\big [ (1+\alpha) \cdot (1+\alpha) \big ] \hspace{0.15cm}{\rm mod} \hspace{0.15cm} p(\alpha) = (\alpha^2 + 1) \hspace{0.15cm}{\rm mod} \hspace{0.15cm} (\alpha^2 + \alpha + 1)= \alpha\hspace{0.05cm}.\]
- Damit existieren für alle Elemente mit Ausnahme des Nullelements die multiplikativen Inversen:
- \[{\rm Inv_M}( 1) = 1 \hspace{0.05cm},\hspace{0.2cm}{\rm Inv_M}(\alpha) = 1+\alpha \hspace{0.05cm},\hspace{0.2cm}{\rm Inv_M}(1+\alpha) = \alpha \hspace{0.05cm}.\]
$\text{Zwischenergebnis:}$
- Die Menge $\{0, 1, \alpha, 1 + \alpha\}$ stellt zusammen mit den zwei Rechenoperationen Addition und Multiplikation modulo $p(\alpha)= \alpha^2 + \alpha + 1$ ein Galoisfeld der Ordnung $q = 4$ dar.
- Dieses mit $\rm GF(2^2) = GF(4)$ bezeichnete Galoisfeld erfüllt alle im vorherigen Kapitel genannten Anforderungen.
- Im Gegensatz zum Zahlenkörper §$\rm GF(3) = \{0, 1, 2\}$ mit der Eigenschaft, dass $q = 3$ eine Primzahl ist, nennt man $\rm GF(2^2)$ einen Erweiterungskörper (englisch: Extension Field).
Reduzible und irreduzible Polynome
Das Polynom $p(\alpha)$ und damit die Bestimmungsgleichung $p(\alpha) = 0$ darf nicht beliebig vorgegeben werden. Das auf der letzten Seite verwendete Polynom $p(\alpha)= \alpha^2 + \alpha + 1$ war geeignet. Nun versuchen wir es mit einem anderen Polynom, nämlich $p(\alpha)= \alpha^2 + 1$.
- $$ \begin{array}{c} {\rm modulo}\hspace{0.15cm}{\it p}(\alpha)= \alpha^2 + 1\\ \end{array}\hspace{0.25cm} \Rightarrow\hspace{0.25cm} \left[ \begin{array}{c|cccccc} + & 0 & 1 & \alpha & 1\!+\!\alpha \\ \hline 0 & 0 & 1 & \alpha & 1\!+\!\alpha \\ 1 & 1 & 0 & 1\!+\!\alpha & \alpha \\ \alpha & \alpha & 1\!+\!\alpha & 0 & 1 \\ 1\!+\!\alpha & 1\!+\!\alpha & \alpha & 1 & 0 \end{array} \right] \hspace{-0.1cm} ,\hspace{0.5cm} \left[ \begin{array}{c|cccccc} \cdot & 0 & 1 & \alpha & 1\!+\!\alpha \\ \hline 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & \alpha & 1\!+\!\alpha \\ \alpha & 0 & \alpha & 1 &1\!+\!\alpha \\ 1\!+\!\alpha & 0 & 1\!+\!\alpha & 1\!+\!\alpha & 0 \end{array} \right] .$$
Die Additionstabelle ist in beiden Fällen identisch und auch die Multiplikationstabellen unterscheiden sich nur durch die vier Einträge in den beiden unteren Zeilen und den beiden hinteren Spalten:
- Aus $p(\alpha) = 0$ folgt nun für das Produkt $\alpha \cdot \alpha = 1$ und das Produkt $(1 +\alpha) \cdot (1 +\alpha) $ ergibt das Nullelement. Das gemischte Produkt $\alpha \cdot (1 +\alpha) = (1 +\alpha) $.
- In der letzten Zeile der Multipliaktionstabelle und auch in der letzten Spalte steht nun keine „$1$” ⇒ Hinsichtlich der Bedingung $p(\alpha)= \alpha^2 + 1= 0$ existiert die multiplikative Inverse zu $1 +\alpha$ nicht.
- Damit erfüllt aber die endliche Menge $\{0, 1, \alpha, 1 + \alpha\}$ zusammen mit Rechenoperationen modulo $p(\alpha)= \alpha^2 + 1$ auch nicht die Voraussetzungen eines Erweiterungskörpers $\rm GF(2^2) $.
$\text{Fassen wir zusammen:}$ Aus dem binären Galoisfeld $\rm GF(2) = \{0, 1\}$ lässt sich unter Zuhilfenahme eines Polynoms vom Grad $m = 2$ mit binären Koeffizienten,
- \[p(x) = x^2 + k_1 \cdot x + k_0 \hspace{0.05cm}, \hspace{0.45cm}k_0\hspace{0.05cm},\hspace{0.1cm}k_1 \in \{0, 1\} \hspace{0.05cm},\]
ein Erweiterungskörper $\rm GF(2^2)$ formulieren. Anmerkung: Die Umbenennung der Funktionsvariablen $\alpha$ in $x$ hat nur formale Bedeutung im Hinblick auf spätere Seiten.
- Im vorliegenden Fall gibt es nur ein geeignetes Polynom $p_1(x)= x^2 + x 1$. Alle anderen möglichen Polynome vom Grad $m = 2$, nämlich
- \[p_2(x) = x^2 + 1 \hspace{0.06cm} = (x+1) \cdot (x+1)\hspace{0.05cm},\]
- \[p_3(x) =x^2 \hspace{0.76cm} = x \cdot x \hspace{0.05cm},\]
- \[p_4(x) = x^2 + x = (x+1) \cdot x\hspace{0.05cm}, \]
lassen sich faktorisieren und ergeben keinen Erweiterungskörper.
- Man nennt die Polynome $p_2(x)$, $p_3(x)$ und $p_4(x)$ reduzibel. Der Schluss liegt nahe, dass für einen Erweiterungskörper nur irreduzible Polynome wie $p_1(x)$ geeignet sind.
Interpretation des neuen Elementes $\alpha$
Wir betrachten weiterhin den Körper ${\rm GF}(2^2) = \{0, 1, \alpha, 1 + \alpha\}$ entsprechend den beiden folgenden Operationstabellen, basierend auf der Nebenbedingung $p(\alpha)= \alpha^2 + \alpha + 1 = 0$ (irreduzibles Ploynom):
- $$ \begin{array}{c} {\rm modulo}\hspace{0.15cm} p(\alpha)= \alpha^2 + \alpha + 1\\ \end{array}\hspace{0.25cm} \Rightarrow\hspace{0.25cm} \left[ \begin{array}{c|cccccc} + & 0 & 1 & \alpha & 1\!+\!\alpha \\ \hline 0 & 0 & 1 & \alpha & 1\!+\!\alpha \\ 1 & 1 & 0 & 1\!+\!\alpha & \alpha \\ \alpha & \alpha & 1\!+\!\alpha & 0 & 1 \\ 1\!+\!\alpha & 1\!+\!\alpha & \alpha & 1 & 0 \end{array} \right] \hspace{-0.1cm} ,\hspace{0.5cm} \left[ \begin{array}{c|cccccc} \cdot & 0 & 1 & \alpha & 1\!+\!\alpha \\ \hline 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & \alpha & 1\!+\!\alpha \\ \alpha & 0 & \alpha & 1\!+\!\alpha & 1 \\ 1\!+\!\alpha & 0 & 1\!+\!\alpha & 1 & \alpha \end{array} \right] .$$
Welche Bedeutung hat aber nun das neue Element $\alpha$?
- Das Polynom $p(\alpha)= \alpha^2 + \alpha + 1 $ hat keine Nullstelle in ${\rm GF}(2) = \{0, 1\}$. Das bedeutet weiter, dass $\alpha$ weder $0$ noch $1$ sein kann.
- Wäre $\alpha= 0$ bzw. $\alpha= 1$, so wären zudem zwei der vier Mengenelemente $\{0, 1, \alpha, 1 + \alpha\}$jeweils identisch. Entweder „$0$” und „$\alpha$” sowie „$1$” und „$1+\alpha$” oder „$1$” und „$\alpha$” sowie „$0$” und „$1+\alpha$”.
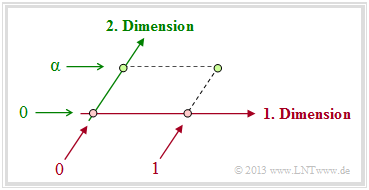
- Vielmehr erhält der eindimensionale Körper ${\rm GF}(2)$ durch die Einführung des Elementes $\alpha$ eine zweite Dimension. Er wird also zum Galoisfeld ${\rm GF}(2^2)$ erweitert, wie die nebenstehende Grafik zeigt.
- Das Element $\alpha$ hat ähnliche Bedeutung wie die imaginäre Einheit ${\rm j}$, durch die man die Menge der reellen Zahlen unter der Nebenbedingung ${\rm j}^2 + 1 = 0$ zur Menge der komplexen Zahlen erweitert.
$\text{Übliche Darstellung des binären Erweiterungskörpers {\rm GF}(2^2):}$
Aufgrund der Identität $\alpha^2 = 1 + \alpha$, die aus der Nebenbedingung $p(\alpha) = 0$ folgt, kann man in gleicher Weise ${\rm GF}(2^2) = \{0, 1, \alpha, \alpha^2\}$schreiben, wobei nun folgende Operationstabellen gelten:
- $$ \begin{array}{c} {\rm modulo}\hspace{0.15cm} p(\alpha)= \alpha^2 + \alpha + 1\\ \end{array}\hspace{0.25cm} \Rightarrow\hspace{0.25cm} \left[ \begin{array}{c\vertcccccc} + & 0 & 1 & \alpha & \alpha^2 \\ \hline 0 & 0 & 1 & \alpha & \alpha^2 \\ 1 & 1 & 0 & \alpha^2 & \alpha \\ \alpha & \alpha & \alpha^2 & 0 & 1 \\ \alpha^2 & \alpha^2 & \alpha & 1 & 0 \end{array} \right] \hspace{-0.1cm} ,\hspace{0.5cm} \left[ \begin{array}{c\vertcccccc} \cdot & 0 & 1 & \alpha & \alpha^2 \\ \hline 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & \alpha & \alpha^2 \\ \alpha & 0 & \alpha &\alpha^2 & 1 \\ \alpha^2 & 0 & \alpha^2 & 1 & \alpha \end{array} \right] .$$
Polynome über einem endlichen Körper
Ein Polynom in einem endlichen Körper GF(P), wobei P eine Primzahl angibt, hat folgende Form:
\[a(x) = \sum_{i = 0}^{m} a_i \cdot x^{i} = a_0 + a_1 \cdot x + a_2 \cdot x^2 + \hspace{0.1cm}... \hspace{0.1cm} + a_m \cdot x^{m} \hspace{0.05cm}.\]
Anzumerken ist:
- Alle Koeffizienten sind Elemente des Körpers: ai ∈ GF(P).
- Ist der führende Koeffizient am ≠ 0, so gibt m den Grad des Polynoms an.
Betrachten wir ein dazu zweites Polynom mit Grad M,
\[b(x) = \sum_{i = 0}^{M} b_i \cdot x^{i} = b_0 + b_1 \cdot x + b_2 \cdot x^2 + \hspace{0.1cm}... \hspace{0.1cm} + b_M \cdot x^{M} \hspace{0.05cm},\]
so erhält man für die Summe (bzw. Differenz) und das Produkt jeweils in GF(P):
\[a(x) \pm b(x) \hspace{-0.15cm} = \hspace{-0.15cm} \sum_{i = 0}^{{\rm max}\hspace{0.05cm}(m, \hspace{0.05cm}M)} \hspace{0.15cm}(a_i \pm b_i) \cdot x^{i} \hspace{0.05cm},\] \[a(x) \cdot b(x) = \hspace{-0.15cm} \sum_{i = 0}^{m + M} \hspace{0.15cm}c_i \cdot x^{i}\hspace{0.05cm},\hspace{0.5cm} c_i = \sum_{j = 0}^{i}\hspace{0.15cm}a_j \cdot b_{i-j} \hspace{0.05cm}.\]
\[s(x) = a(x) + b(x) = x^3 + x^2 \hspace{0.05cm}, \hspace{0.5cm} d(x) = a(x) - b(x) = x^3 + x^2 = s(x)\hspace{0.05cm},\]
\[c(x) = a(x) \cdot b(x) =\sum_{i = 0}^{3 + 2} \hspace{0.15cm}c_i \cdot x^{i}\hspace{0.05cm},\hspace{0.5cm} c_i = \sum_{j = 0}^{i}\hspace{0.15cm}a_j \cdot b_{i-j} \hspace{0.05cm}.\]
Mit a0 = a1 = a3 = b0 = b1 = b2 = 1 und a2 = a4 = a5 = b3 = b4 = b5 = 0 erhält man:
\[c_0 \hspace{-0.25cm} = \hspace{-0.15cm} a_0 \cdot b_0 = 1 \cdot 1 = 1 \hspace{0.05cm},\] \[c_1 \hspace{-0.25cm} = \hspace{-0.15cm} a_0 \cdot b_1 + a_1 \cdot b_0 = 1 \cdot 1 + 1 \cdot 1 = 0 \hspace{0.05cm},\] \[c_2 \hspace{-0.25cm} = \hspace{-0.15cm} a_0 \cdot b_2 + a_1 \cdot b_1 + a_2 \cdot b_0 = 1 \cdot 1 + 1 \cdot 1 + 0 \cdot 1 = 0 \hspace{0.05cm},\] \[c_3 \hspace{-0.25cm} = \hspace{-0.15cm} a_0 \cdot b_3 + a_1 \cdot b_2 + a_2 \cdot b_1 + a_3 \cdot b_0 = 1 \cdot 0 + 1 \cdot 1 + 0 \cdot 1 + 1 \cdot 1 = 0 \hspace{0.05cm},\] \[c_4 \hspace{-0.25cm} = \hspace{-0.15cm} a_0 \cdot b_4 + a_1 \cdot b_3 + \hspace{0.05cm}...+ \hspace{0.05cm}a_4 \cdot b_0 =1 \cdot 0 + 1 \cdot 0 + 0 \cdot 1 + 1 \cdot 1 + 0 \cdot 1 = 1 \hspace{0.05cm},\] \[c_5 \hspace{-0.25cm} = \hspace{-0.15cm} a_0 \cdot b_5 + a_1 \cdot b_4 + \hspace{0.05cm}...+ \hspace{0.05cm} a_5 \cdot b_0 =1 \cdot 0 + 1 \cdot 0 + 0 \cdot 0 + 1 \cdot 1 + 0 \cdot 1 + 0 \cdot 1= 1 \]
\[\Rightarrow \hspace{0.3cm} c(x) = x^5 + x^4 +1 \hspace{0.05cm}.\]
Im Galoisfeld GF(3) erhält man aufgrund der Modulo–3–Operationen andere Ergebnisse:
\[s(x) \hspace{-0.15cm} = \hspace{-0.15cm} (x^3 + x + 1) + (x^2 + x + 1) = x^3 + x^2 + 2x + 2\hspace{0.05cm},\] \[d(x) \hspace{-0.15cm} = \hspace{-0.15cm} x^3 + x + 1) - (x^2 + x + 1) = x^3 + 2x^2 \hspace{0.05cm},\]
\[c(x) \hspace{-0.15cm} = \hspace{-0.15cm} x^3 + x + 1) \cdot (x^2 + x + 1) = x^5 + x^4 + 2x^3 + 2x^2 + 2x +1\hspace{0.05cm}.\]
Polynome über einem endlichen Körper (2)
\[a(x) = p(x) \cdot q(x) \hspace{0.05cm}.\]
Ist diese Faktorisierung nicht möglich, das heißt, wenn
\[a(x) = p(x) \cdot q(x) + r(x)\hspace{0.05cm},\hspace{0.5cm} r(x) \ne 0\]
gilt, so spricht man von einem irreduziblen (englisch: irreducible oder prime) Polynom.
Im rechten Teil der obigen Grafik ist die Modulo–2–Division q(x) = a(x)/p2(x) mit dem Ergebnis q(x) = x3 + x2 + x + 1 dargestellt. Es verbleibt der Rest r(x) = x. Allein nach dieser Rechnung könnte a(x) = x5 + x4 + 1 durchaus ein irreduzibles Polynom sein.
Der Nachweis, dass das Polynom a(x) = x5 + x4 + 1 tatsächlich irreduzibel ist, wäre allerdings erst dann erbracht, wenn a(x)/p(x) für alle
\[p(x) = \sum_{i = 0}^{m} a_i \cdot x^{i} = a_m \cdot x^{m} + a_{m-1} \cdot x^{m-1} + \hspace{0.1cm}... \hspace{0.1cm}+ a_2 \cdot x^2 + a_1 \cdot x + a_0 \hspace{0.05cm}\]
einen Rest r(x) ≠ 0 liefert. Dies würde im vorliegenden Beispiel (nahezu) 25 = 32 Divisionen erfordern.
Verallgemeinerte Definition eines Erweiterungskörpers
Wir gehen von folgenden Voraussetzungen aus:
- einem Galoisfeld GF(P), wobei P eine Primzahl angibt,
- einem irreduziblen Polynom p(x) über GF(P) mit dem Grad m:
\[p(x) = a_m \cdot x^{m} + a_{m-1} \cdot x^{m-1} + \hspace{0.1cm}... \hspace{0.1cm}+ a_2 \cdot x^2 + a_1 \cdot x + a_0 \hspace{0.05cm}, \hspace{0.3cm} a_i \in {\rm G}(P)\hspace{0.05cm}, \hspace{0.15cm}a_m \ne 0\hspace{0.05cm}. \]
Mit den genannten Voraussetzungen gilt allgemein:
\[{\rm GF}(P^m)= \Big\{ k_{m-1} \hspace{0.01cm}\cdot \hspace{0.02cm}\alpha^{m-1} \hspace{0.05cm}+ \hspace{0.05cm}... \hspace{0.05cm}+ \hspace{0.05cm}k_1 \hspace{0.01cm}\cdot \hspace{0.02cm} \alpha \hspace{0.05cm}+ \hspace{0.05cm} k_0\hspace{0.05cm} \Big{|}\hspace{0.02cm} \ k_i\in{\rm GF}(P) = \{ 0, 1, \hspace{0.05cm}... \hspace{0.05cm}, P-1\}\Big \}\]
Die Addition und Multiplikation in diesem Erweiterungskörper entspricht dann der Polynomaddition und Polynommultiplikation modulo p(α).
Ein Galoisfeld GF(q) mit q Elementen lässt sich also immer dann angeben, wenn die Elementenanzahl in der Form q = Pm geschrieben werden kann (P kennzeichnet eine Primzahl, m sei ganzzahlig).
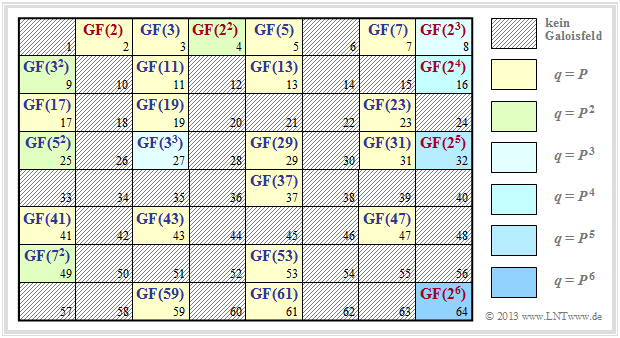
Die Grafik zeigt, für welche q–Werte sich jeweils ein Galoisfeld konstruieren lässt. Für die schraffiert eingezeichneten q–Werte ist kein endlicher Körper angebbar. Weiter ist anzumerken:
- Die gelb hinterlegten Positionen q = P ⇒ m = 1 markieren Zahlenmengen {0, 1, ... , q – 1} mit Galoiseigenschaften, siehe Kapitel 2.1.
- Die anderen farblich hinterlegten Positionen markieren Erweiterungskörper mit q = Pm, m ≥ 2. Für q ≤ 64 basieren diese auf den Primzahlen 2, 3, 5 und 7.
- Mit roter Schrift hervorgehoben sind binäre Körper ⇒ q = 2m, m ≥ 1, die auf der nächsten Seite noch genauer betrachtet werden. Alle anderen Erweiterungskörper sind blau beschriftet.
Binäre Erweiterungskörper (1)
Im Folgenden betrachten wir binäre Erweiterungskörper mit
\[q = 2^m \hspace{0.15cm}(m \ge 2) \hspace{0.3cm} \Rightarrow\hspace{0.3cm} q = 4, 8, 16, 32, 64, ...\]
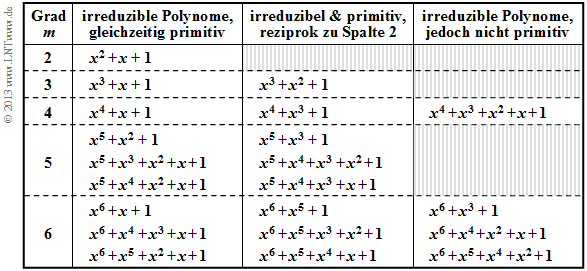
Elementen. In der Tabelle sind für 2 ≤ m ≤ 6 alle irreduziblen Polynome des Galoisfeldes GF(2) angegeben. Die Polynome in Spalte 2 und 3 sind nicht nur irreduzibel, sondern auch primitiv.
Bevor wir uns der Definition eines primitiven Polynoms zuwenden, sollen zunächst die Besonderheiten primitiver Elemente am Beispiel von
\[{\rm GF}(q) = \{\hspace{0.05cm}z_0 = 0,\hspace{0.1cm} z_1 = 1,\hspace{0.1cm} ... , \hspace{0.05cm}z_{q-1}\}\]
genannt werden. Das Element zi = β wird dann als primitiv bezeichnet,
- wenn die Potenz β i modulo q zum ersten Mal für i = q – 1 das Ergebnis „1” liefert,
- so dass β i für 1 ≤ i ≤ q – 1 genau die Elemente z1, ... , zq–1 liefert, also alle Elemente von GF(q) mit Ausnahme des Nullelementes z0 = 0.
\[2^1 \hspace{-0.1cm} = \hspace{-0.1cm} 2\hspace{0.05cm},\hspace{0.2cm} 2^2 = 4\hspace{0.05cm},\hspace{0.2cm} 2^3 = 8 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 3\hspace{0.05cm},\hspace{0.2cm} 2^4 = 16 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.05cm},\] \[3^1 \hspace{-0.1cm} = \hspace{-0.1cm} 3\hspace{0.05cm},\hspace{0.2cm} 3^2 = 9\hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 4\hspace{0.05cm},\hspace{0.2cm} 3^3 = 27 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 2\hspace{0.05cm},\hspace{0.2cm} 3^4 = 81 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\]
primitive Elemente. Dagegen ist „4” kein primitives Element, weil bereits 42 = 1 ist:
\[4^1 = 4\hspace{0.05cm},\hspace{0.2cm} 4^2 = 16 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.05cm},\hspace{0.2cm} 4^3 = 64 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 4\hspace{0.05cm},\hspace{0.2cm} 4^4 = 256 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.05cm}.\]
Primitive Polynome
Alle in Spalte 2 der obigen Tabelle angegebenen Polynome sind sowohl irreduzibel als auch primitiv. Ist p1(x) ein primitives Polynom, so ist auch das dazu reziproke Polynom
\[p_2 (x) = x^m \cdot p_1(x^{-1})\]
primitiv. Alle Polynome in Spalte 3 sind reziprok zum Polynom in Spalte 2. Beispielsweise gilt für m = 3:
\[p_1(x) = x^3 + x + 1 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}p_2(x) = x^3 \cdot [x^{-3} + x^{-1} + 1 ]= x^3 + x^2 + 1 \hspace{0.05cm}.\]
Die irreduziblen Polynome der Spalte 4 sind dagegen nicht primitiv; sie spielen nur eine untergeordnete Rolle zur Beschreibung von Fehlerkorrekturverfahren.
Hinweis: Primitive Polynome liefern auch die Grundlage für Pseudo–Noise–Generatoren.
- das Galoisfeld GF(23) = GF(8), sowie
- das Polynom p(x) = x3 + x + 1.
Aus der Bedingung p(α) = 0 erhält man in GF(23) weiter:
\[\alpha^3 + \alpha + 1 = 0 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}\alpha^3 = \alpha + 1 \hspace{0.05cm},\]
und damit für die Potenzen αi der Wurzel für i ≥ 4:
\[\alpha^4 \hspace{-0.15cm} = \hspace{-0.15cm} \alpha \cdot \alpha^3 = \alpha \cdot (\alpha + 1) = \alpha^2 + \alpha \hspace{0.05cm},\] \[\alpha^5 \hspace{-0.15cm} = \hspace{-0.15cm} \alpha^2 \cdot \alpha^3 = \alpha^2 \cdot (\alpha + 1) = \alpha^3 + \alpha^2 = \alpha^2 + \alpha + 1 \hspace{0.05cm},\] \[\alpha^6 \hspace{-0.15cm} = \hspace{-0.15cm} \alpha^3 \cdot \alpha^3 = (\alpha + 1) \cdot (\alpha + 1) = \alpha^2 + \alpha + \alpha + 1= \alpha^2 + 1 \hspace{0.05cm},\]
\[\alpha^7 \hspace{-0.15cm} = \hspace{-0.15cm} \alpha^4 \cdot \alpha^3 = (\alpha^2 + \alpha) \cdot (\alpha + 1) = \alpha^3 + \alpha^2 + \alpha^2 + \alpha = \alpha + 1 + \alpha = 1 = \alpha^0 \hspace{0.05cm}.\]Binäre Erweiterungskörper (3)
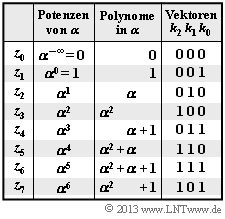 Die Elemente z0, z1, ... , z7 des Galoisfeldes GF(23) lassen sich entsprechend der nebenstehenden Tabelle wie folgt darstellen:
Die Elemente z0, z1, ... , z7 des Galoisfeldes GF(23) lassen sich entsprechend der nebenstehenden Tabelle wie folgt darstellen:
- als Potenzen von α (Exponentendarstellung),
- als Polynome der Form k2 · α2 + k1 · α + k0 mit binären Koeffizienten k2, k1, k0 (jeweils 0 oder 1) ,
- als Vektoren der Koeffizienten (k2, k1, k0).
Für die Addition (oder Subtraktion) zweier Elemente eignen sich die Polynom– und die Vektordarstellung gleichermaßen, wobei die Komponenten modulo 2 zu addieren sind, zum Beispiel:
\[z_5 + z_7 \hspace{-0.15cm} = \hspace{-0.15cm} (\alpha^2 + \alpha) + (\alpha^2 + 1) = \alpha + 1 = \alpha^3 = z_4 \hspace{0.05cm},\] \[{\rm oder}\hspace{0.15cm} z_5 + z_7 \hspace{-0.15cm} = \hspace{-0.15cm} (110) + (101) = (011) = z_4 \hspace{0.05cm},\] \[\hspace{0.15cm} z_1 + z_2 + z_3 \hspace{-0.15cm} = \hspace{-0.15cm} (001) + (010) + (100)= (111) = z_6 \hspace{0.05cm}.\]
Für Multiplikationen ist die Exponentendarstellung besser geeignet, wie die folgenden Beispiele zeigen:
\[z_3 \cdot z_4 \hspace{-0.15cm} = \hspace{-0.15cm} \alpha^2 \cdot \alpha^3 = \alpha^{2+3}= \alpha^{5} = z_6 \hspace{0.05cm},\] \[z_0 \cdot z_5 \hspace{-0.15cm} = \hspace{-0.15cm} \alpha^{-\infty} \cdot \alpha^4 = \alpha^{-\infty} = z_0 \hspace{0.05cm},\] \[z_5 \cdot z_7 \hspace{-0.15cm} = \hspace{-0.15cm} \alpha^4 \cdot \alpha^6 = \alpha^{10}= \alpha^{7} \cdot \alpha^{3} = 1 \cdot \alpha^{3}= z_4 \hspace{0.05cm}.\]
Man erkennt, dass sich hierbei die Exponenten modulo (q – 1) ergeben; im Beispiel modulo 7.
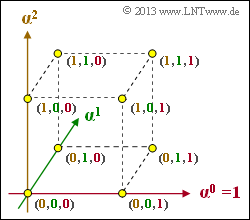 Die Grafik zeigt den endlichen Erweiterungskörper GF(23) in einer 3D–Darstellung, wobei die Achsen mit α0 = 1, α1 und α2 bezeichnet sind. Die 23 = 8 Punkte im dreidimensionalen Raum sind mit den Koeffizientenvektoren beschriftet, wobei die Zuordnung der einzelnen Koeffizienten k2, k1, k0 zu den Achsen farblich deutlich gemacht ist.
Die Grafik zeigt den endlichen Erweiterungskörper GF(23) in einer 3D–Darstellung, wobei die Achsen mit α0 = 1, α1 und α2 bezeichnet sind. Die 23 = 8 Punkte im dreidimensionalen Raum sind mit den Koeffizientenvektoren beschriftet, wobei die Zuordnung der einzelnen Koeffizienten k2, k1, k0 zu den Achsen farblich deutlich gemacht ist.
Aufgaben zum Kapitel
A2.3 Reduzible und irreduzible Polynome
Zusatzaufgaben:2.3 Polynomdivision
A2.4 GF(2^2)–Darstellungsformen
Zusatzaufgaben:2.4 Endliche und unendliche Körper
A2.5 Drei Varianten von GF(2^4)
Zusatzaufgaben:2.5 Einige Berechnungen über GF(2^3)
A2.6 GF(P^m). Welches P, welches m?