Difference between revisions of "Aufgaben:Exercise 3.1Z: Convolution Codes of Rate 1/2"
(Die Seite wurde neu angelegt: „{{quiz-Header|Buchseite=Kanalcodierung/Grundlagen der Faltungscodierung }} [[File:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice Fr…“) |
|||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite=Kanalcodierung/Grundlagen der Faltungscodierung | + | {{quiz-Header|Buchseite=Kanalcodierung/Grundlagen der Faltungscodierung}} |
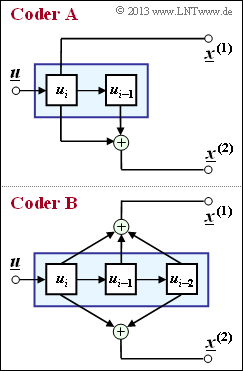
| + | [[File:P_ID2589__KC_Z_3_1.png|right|frame|Zwei Faltungscodes der Rate 1/2]] | ||
| + | Die Grafik zeigt zwei Faltungscodierer der Rate $R = 1/2$. Am Eingang liegt die Informationssequenz $\underline {u} = (u_1, u_2, \ ... \ , u_i, \ ...$) an. Hieraus werden durch Modulo–2–Operationen die beiden Sequenzen | ||
| + | :$$\underline{\it x}^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \big( \hspace{0.05cm}x_1^{(1)}\hspace{0.05cm},\hspace{0.05cm} x_2^{(1)}\hspace{0.05cm},\hspace{0.05cm} ... \hspace{0.05cm},\hspace{0.05cm} | ||
| + | x_i^{(1)} \hspace{0.05cm}, ... \hspace{0.05cm} \big )\hspace{0.05cm},$$ | ||
| + | :$$\underline{\it x}^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \big( \hspace{0.05cm}x_1^{(2)}\hspace{0.05cm},\hspace{0.05cm} x_2^{(2)}\hspace{0.05cm},\hspace{0.05cm} ... \hspace{0.05cm},\hspace{0.05cm} | ||
| + | x_i^{(2)} \hspace{0.05cm}, ... \hspace{0.05cm} \big )$$ | ||
| + | erzeugt, wobei $x_i^{(j)}$ mit $j = 1$ bzw. $j = 2$ außer von $u_i$ auch von den vorherigen Informationsbits $u_{i–1}, \ ... \ , u_{i \, –m}$ abhängen kann. Man bezeichnet $m$ als das Gedächtnis und $\nu = m + 1$ als die Einflusslänge des Codes bzw. des Codierers. Die betrachteten Coder <span style="color: rgb(204, 0, 0);"><b>A</b></span> und <span style="color: rgb(204, 0, 0);"><b>B</b></span> unterscheiden sich hinsichtlich dieser Größen. | ||
| + | In der Grafik nicht dargestellt ist das Multiplexen der beiden Teilsequenzen $\underline {x}^{(1)}$ und $\underline {x}^{(2)}$ zur resultierenden Codesequenz $\underline {x} = (x_1^{(1)}, x_1^{(2)}, x_2^{(1)}, x_2^{(2)}, \ ...)$. | ||
| − | }} | + | In den Teilaufgaben (3) bis (5) sollen Sie den jeweiligen Beginn der Sequenzen $\underline {x}^{(1)}, \underline{x}^{(2)}$ und $\underline{x}$ ermitteln, wobei von der Informationssequenz $\underline{u} = (1, 0, 1, 1, 0, 0, \ ...)$ auszugehen ist. |
| + | |||
| + | ''Hinweise:'' | ||
| + | * Die Aufgabe bezieht sich auf das Themengebiet des Kapitels [[Kanalcodierung/Grundlagen_der_Faltungscodierung| Grundlagen der Faltungscodierung]]. | ||
| + | * Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.$$ | ||
| − | |||
===Fragebogen=== | ===Fragebogen=== | ||
| − | |||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Multiple-Choice | + | {Multiple-Choice |
|type="[]"} | |type="[]"} | ||
| − | + | + correct | |
| − | + | + | - false |
| − | |||
{Input-Box Frage | {Input-Box Frage | ||
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $xyz \ = \ ${ 5.4 3% } $ab$ |
| − | |||
| − | |||
| − | |||
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' |
| − | '''2 | + | '''(2)''' |
| − | '''3 | + | '''(3)''' |
| − | '''4 | + | '''(4)''' |
| − | '''5 | + | '''(5)''' |
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | + | [[Category:Aufgaben zu Kanalcodierung|^3.1 Grundlagen der Faltungscodierung^]] | |
| − | [[Category:Aufgaben zu Kanalcodierung|^3.1 Grundlagen der Faltungscodierung | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ^]] | ||
Revision as of 13:25, 22 November 2017
Die Grafik zeigt zwei Faltungscodierer der Rate $R = 1/2$. Am Eingang liegt die Informationssequenz $\underline {u} = (u_1, u_2, \ ... \ , u_i, \ ...$) an. Hieraus werden durch Modulo–2–Operationen die beiden Sequenzen
- $$\underline{\it x}^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \big( \hspace{0.05cm}x_1^{(1)}\hspace{0.05cm},\hspace{0.05cm} x_2^{(1)}\hspace{0.05cm},\hspace{0.05cm} ... \hspace{0.05cm},\hspace{0.05cm} x_i^{(1)} \hspace{0.05cm}, ... \hspace{0.05cm} \big )\hspace{0.05cm},$$
- $$\underline{\it x}^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \big( \hspace{0.05cm}x_1^{(2)}\hspace{0.05cm},\hspace{0.05cm} x_2^{(2)}\hspace{0.05cm},\hspace{0.05cm} ... \hspace{0.05cm},\hspace{0.05cm} x_i^{(2)} \hspace{0.05cm}, ... \hspace{0.05cm} \big )$$
erzeugt, wobei $x_i^{(j)}$ mit $j = 1$ bzw. $j = 2$ außer von $u_i$ auch von den vorherigen Informationsbits $u_{i–1}, \ ... \ , u_{i \, –m}$ abhängen kann. Man bezeichnet $m$ als das Gedächtnis und $\nu = m + 1$ als die Einflusslänge des Codes bzw. des Codierers. Die betrachteten Coder A und B unterscheiden sich hinsichtlich dieser Größen.
In der Grafik nicht dargestellt ist das Multiplexen der beiden Teilsequenzen $\underline {x}^{(1)}$ und $\underline {x}^{(2)}$ zur resultierenden Codesequenz $\underline {x} = (x_1^{(1)}, x_1^{(2)}, x_2^{(1)}, x_2^{(2)}, \ ...)$.
In den Teilaufgaben (3) bis (5) sollen Sie den jeweiligen Beginn der Sequenzen $\underline {x}^{(1)}, \underline{x}^{(2)}$ und $\underline{x}$ ermitteln, wobei von der Informationssequenz $\underline{u} = (1, 0, 1, 1, 0, 0, \ ...)$ auszugehen ist.
Hinweise:
- Die Aufgabe bezieht sich auf das Themengebiet des Kapitels Grundlagen der Faltungscodierung.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.$$
Fragebogen
Musterlösung