Difference between revisions of "Channel Coding/Definition and Properties of Reed-Solomon Codes"
| Line 221: | Line 221: | ||
*Erste Zeile, erste Spalte: | *Erste Zeile, erste Spalte: | ||
| − | ::<math>1 \hspace{0.1cm} \cdot \hspace{0.1cm} \big [1 + \alpha^1 + \alpha^2 + \alpha^3 + \alpha^4 + \alpha^5 + \alpha^6 \big ] = 1 + \alpha + \alpha^2 + (\alpha + 1) + (\alpha^2 + \alpha)+ (\alpha^2 + \alpha +1)+ (\alpha^2 + 1) = 0 \hspace{0.05cm} | + | ::<math>1 \hspace{0.1cm} \cdot \hspace{0.1cm} \big [1 + \alpha^1 + \alpha^2 + \alpha^3 + \alpha^4 + \alpha^5 + \alpha^6 \big ] = 1 + \alpha + \alpha^2 + (\alpha + 1) + (\alpha^2 + \alpha)+ (\alpha^2 + \alpha +1)+ (\alpha^2 + 1) = 0 \hspace{0.05cm}; </math> |
*Letzte Zeile, letzte Spalte: | *Letzte Zeile, letzte Spalte: | ||
| Line 227: | Line 227: | ||
::<math>1 \hspace{0.1cm} \cdot \hspace{0.1cm} 1 + \alpha^2 \cdot \alpha^4 + \alpha^4 \cdot \alpha^1 | ::<math>1 \hspace{0.1cm} \cdot \hspace{0.1cm} 1 + \alpha^2 \cdot \alpha^4 + \alpha^4 \cdot \alpha^1 | ||
+ \alpha^6 \cdot \alpha^5+ \alpha^1 \cdot \alpha^2+ \alpha^3 \cdot \alpha^6+ \alpha^5 \cdot \alpha^3= 1 + \alpha^6 + \alpha^5 + \alpha^{11} + \alpha^{3}+ \alpha^{9}+ \alpha^{8} =</math> | + \alpha^6 \cdot \alpha^5+ \alpha^1 \cdot \alpha^2+ \alpha^3 \cdot \alpha^6+ \alpha^5 \cdot \alpha^3= 1 + \alpha^6 + \alpha^5 + \alpha^{11} + \alpha^{3}+ \alpha^{9}+ \alpha^{8} =</math> | ||
| − | ::<math> \hspace{ | + | ::<math> \hspace{1.5cm} = \hspace{0.15cm} 1 + \alpha^6 + \alpha^5 + \alpha^{4} + \alpha^{3}+ \alpha^{2}+ \alpha^{1} =0 \hspace{0.05cm}.</math>}}<br> |
== Singleton–Schranke und minimale Distanz == | == Singleton–Schranke und minimale Distanz == | ||
<br> | <br> | ||
| − | Eine wichtige Kenngröße eines jeden Blockcodes ist die [ | + | Eine wichtige Kenngröße eines jeden Blockcodes ist die [[Kanalcodierung/Zielsetzung_der_Kanalcodierung#Einige_wichtige_Definitionen_zur_Blockcodierung| minimale Distanz]] zwischen zwei beliebigen Codeworten $\underline {c}_i$ und $\underline {c}_j$. |
| + | *Die Reed–Solomon–Codes gehören zur Klasse der <i>linearen</i> und <i>zyklischen</i> Codes. Bei diesen kann man vom Nullwort $\underline {c}_0 = (0, 0, \hspace{0.05cm} \text{...} \hspace{0.05cm}, 0)$ als Bezugsgröße ausgehen. | ||
| + | *Aus der Anzahl der Nullen in den anderen Codeworten $\underline {c}_j ≠ \underline {c}_0$ lässt sich das [[Kanalcodierung/Schranken_f%C3%BCr_die_Blockfehlerwahrscheinlichkeit#Distanzspektrum_eines_linearen_Codes_.282.29| Distanzspektrum]] $\{ \hspace{0.05cm}W_j\hspace{0.05cm}\}$ angeben.<br> | ||
| − | {{Beispiel} | + | {{GraueBox|TEXT= |
| + | $\text{Beispiel 5:}$ Die Tabelle verdeutlicht die Bestimmung des Distanzspektrums für den '''RSC (3, 2, 2)<sub>4</sub>'''. | ||
| + | *Gegenüber den bisherigen Grafiken wird die Symbolmenge vereinfachend mit $\{0, 1, 2, 3\}$ anstelle von $\{0, \alpha^0, \alpha^1, \alpha^2\}$ bezeichnet. | ||
| + | *Die Distanz $d$ zwischen $\underline {c}_j$ und dem Nullwort &$\underline {c}_0$ ist identisch dem [[Kanalcodierung/Zielsetzung_der_Kanalcodierung#Einige_wichtige_Definitionen_zur_Blockcodierung|Hamming–Gewicht]] $w_{\rm H}(\underline {c}_j)$.<br> | ||
| − | [[File:P ID2520 KC T 2 3 S3 v1.png|Zur Herleitung des Distanzspektrums für den RSC (3, 2, 2)<sub>4</sub>|class=fit]] | + | [[File:P ID2520 KC T 2 3 S3 v1.png|center|frame|Zur Herleitung des Distanzspektrums für den RSC (3, 2, 2)<sub>4</sub>|class=fit]] |
| − | Neun der Codeworte unterscheiden sich vom Nullwort in zwei Symbolen und sechs Codeworte in drei Symbolen: | + | Aus der oberen Tabelle kann unter anderem abgelesen werden: |
| + | *Neun der Codeworte unterscheiden sich vom Nullwort in zwei Symbolen und sechs Codeworte in drei Symbolen: $W_2 = 9$, $W_3 = 6$. | ||
| + | *Es gibt kein einziges Codewort mit nur einer Null. Das heißt: Die minimale Distanz beträgt hier $d_{\rm min} = 2$. <br> | ||
| − | |||
| − | + | Aus der unteren Tabelle erkennt man, dass auch für die Binärdarstellung $d_{\rm min} = 2$ gilt.}}<br> | |
| − | |||
| − | + | Dieses empirische Ergebnis soll nun verallgemeinert werden: | |
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Ohne Beweis:}$ | ||
| + | *Die <i>minimale Distanz</i> eines jeden $(n, k)$–Reed–Solomon–Codes beträgt $d_{\rm min} =n-k+1$. Damit lassen sich $e = d_{\rm min} -1 =n-k$ Symbolfehler erkennen.<br> | ||
| − | * | + | *Bei <i>fehlerkorrigierenden Codes</i> wählt man meist ein $d_{\rm min} $ ungeradzahlig ⇒ $n-k$ geradzahlig. Bei RS–Codes können dann bis zu $t =(n-k)/2$ Symbolfehler korrigiert werden.<br> |
| − | ::<math>W_i = {n \choose i} \cdot \sum_{j = 0}^{i-d}\hspace{0.15cm}(-1)^j \cdot {i \choose j} \cdot \ | + | *Die [https://de.wikipedia.org/wiki/Singleton-Schranke Singleton–Schranke] besagt, dass für alle linearen Codes $d_{\rm min} \le n-k+1$ gilt. RS–Codes erreichen diese Schranke mit Gleichheit; sie sind so genannte [https://de.wikipedia.org/wiki/MDS-Code MDS–Codes] (<i>Maximum Distance Separable</i>). |
| + | |||
| + | *Das [[Kanalcodierung/Schranken_f%C3%BCr_die_Blockfehlerwahrscheinlichkeit#Distanzspektrum_eines_linearen_Codes| Distanzspektrum]] setzt sich zusammen aus $W_0 = 1$ sowie weiteren Gewichtsfaktoren $W_i$ mit $d ≤ i ≤ n$, wobei in der folgenden Gleichung $d_{\rm min}$ mit $d$ abgekürzt ist: | ||
| + | |||
| + | ::<math>W_i = {n \choose i} \cdot \sum_{j = 0}^{i-d}\hspace{0.15cm}(-1)^j \cdot {i \choose j} \cdot \bigg [\hspace{0.03cm}q^{i\hspace{0.03cm}-\hspace{0.03cm}j\hspace{0.03cm}-\hspace{0.03cm}d\hspace{0.03cm}+\hspace{0.03cm}1}-1 \hspace{0.03cm} \bigg ]\hspace{0.05cm}.</math>}} | ||
== Codebezeichnung und Coderate == | == Codebezeichnung und Coderate == | ||
| Line 281: | Line 292: | ||
:<math>W_0 = 1\hspace{0.05cm}, \hspace{0.2cm}W_2 = 9\hspace{0.05cm}, \hspace{0.2cm}W_3 = 6\hspace{0.3cm}\Rightarrow\hspace{0.3cm}W(X) = 1 + 9 \cdot X^2 + 6 \cdot X^3\hspace{0.05cm}.</math> | :<math>W_0 = 1\hspace{0.05cm}, \hspace{0.2cm}W_2 = 9\hspace{0.05cm}, \hspace{0.2cm}W_3 = 6\hspace{0.3cm}\Rightarrow\hspace{0.3cm}W(X) = 1 + 9 \cdot X^2 + 6 \cdot X^3\hspace{0.05cm}.</math> | ||
| − | [[File:P ID2521 KC T 2 3 S3 v1.png|Herleitung der Distanzspektren von RSC (3, 2, 2) <sub>4</sub> und RSC (6, 4, 2)<sub>2</sub>|class=fit]] | + | [[File:P ID2521 KC T 2 3 S3 v1.png|center|frame|Herleitung der Distanzspektren von RSC (3, 2, 2) <sub>4</sub> und RSC (6, 4, 2)<sub>2</sub>|class=fit]] |
Die binäre Repräsentation des Codes RSC (3, 2, 2)<sub>4</sub> führt zum RSC (6, 4, 2)<sub>2</sub>, ebenfalls mit der Rate <i>R</i> = 4/6 = 2/3 und der Minimaldistanz <i>d</i><sub>min</sub> = 2. Es ergibt sich allerdings ein anderes Distanzspektrum: | Die binäre Repräsentation des Codes RSC (3, 2, 2)<sub>4</sub> führt zum RSC (6, 4, 2)<sub>2</sub>, ebenfalls mit der Rate <i>R</i> = 4/6 = 2/3 und der Minimaldistanz <i>d</i><sub>min</sub> = 2. Es ergibt sich allerdings ein anderes Distanzspektrum: | ||
Revision as of 14:42, 22 November 2017
Contents
Definition und Eigenschaften der Reed–Solomon–Codes
Ein Reed–Solomon–Code – im Folgenden manchmal auch verkürzt als RS–Code bezeichnet – ist ein linearer Blockcode, der einem Informationsblock $\underline{u}$ mit $k$ Symbolen ein entsprechendes Codewort $\underline{c}$ mit $n > k$ Symbolen zuordnet. Diese noch heute vielfach eingesetzten Codes wurden bereits Anfang der 1960er Jahre von Irving Stoy Reed und Gustave Solomon erfunden.
Im Kapitel Zielsetzung der Kanalcodierung wurde der Informationsblock mit $\underline{u}= (u_1,$ ... , $u_k)$ und das Codewort mit $\underline{x}= (x_1,$ ... , $x_n)$ bezeichnet. Die Nomenklaturänderung gemäß obiger Grafik wurde vorgenommen, um Verwechslungen mit dem Argument von Polynomen auszuschließen und die Beschreibung der RS–Codes zu vereinfachen.
Alle im Abschnitt Lineare Codes und zyklische Codes genannten Eigenschaften linearer zyklischer Blockcodes gelten auch für einen Reed–Solomon–Code. Zusätzlich gilt:
- Konstruktion und Decodierung von Reed–Solomon–Codes basieren auf der Arithmetik eines Galoisfeldes ${\rm GF}(q)$, wobei wir uns hier auf binäre Erweiterungskörper mit $q=2^m$ Elementen beschränken:
- \[{\rm GF}(2^m) = \big \{\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.1cm} \alpha^{0} ,\hspace{0.05cm}\hspace{0.1cm} \alpha^{1}\hspace{0.05cm},\hspace{0.1cm} \alpha^{2}\hspace{0.05cm},\hspace{0.1cm}...\hspace{0.1cm}, \alpha^{q-2}\hspace{0.05cm} \big \}\hspace{0.05cm}. \]
- Prinzipiell unterschiedlich zum ersten Kapitel ist, dass die Koeffizienten $u_0$, $u_1$, ... , $u_{k-1}$ nun nicht mehr einzelne Informationsbits ($0$ oder $1$) angeben, sondern ebenfalls Elemente aus ${\rm GF}(2^m)$ sind. Jedes der $n$ Symbole steht vielmehr für $m$ Bit.
- Bei den Reed–Solomon–Codes ist der Parameter $n$ (Codelänge) gleich der Anzahl der Elemente des Galoisfeldes ohne das Nullwort: $n= q-1$. Wir verwenden hierzu folgende Nomenklatur:
- \[{\rm GF}(2^m) \hspace{-0.05cm}\setminus \hspace{-0.05cm} \{0\} = \big \{\hspace{0.05cm} \alpha^{0} ,\hspace{0.05cm}\hspace{0.1cm} \alpha^{1}\hspace{0.05cm},\hspace{0.1cm} \alpha^{2}\hspace{0.05cm},\hspace{0.1cm}...\hspace{0.1cm}, \alpha^{n-1}\hspace{0.05cm} \big \}\hspace{0.05cm}. \]
- Die $k$ Koeffizienten $u_i \in {\rm GF}(2^m)$ des Informationsblocks $\underline{u} \ ( 0 \le i < k)$ kann man formal auch durch ein Polynom $u(x)$ ausdrücken. Der Grad des Polynoms ist dabei $k-1$:
- \[u(x) = \sum_{i = 0}^{k-1} u_i \cdot x^{i} = u_0 + u_1 \cdot x + u_2 \cdot x^2 + \hspace{0.1cm}... \hspace{0.1cm}+ u_{k-1} \cdot x^{k-1} \hspace{0.05cm},\hspace{0.4cm} u_i \in {\rm GF}(2^m) \hspace{0.05cm}.\]
- Die $n$ Symbole des zugehörigen Codewortes $\underline{c}= (c_0, c_1,$ ... , $c_{n-1})$ergeben sich mit diesem Polynom $u(x)$ zu
- \[c_0 = u(\alpha^{0}) \hspace{0.05cm},\hspace{0.3cm} c_1 = u(\alpha^{1})\hspace{0.05cm},\hspace{0.1cm}...\hspace{0.1cm},\hspace{0.3cm} c_{n-1}= u(\alpha^{n-1}) \hspace{0.05cm}.\]
- Meist werden die Codesymbole $c_i \in {\rm GF}(2^m)$ vor der Übertragung wieder in Binärform ⇒ ${\rm GF}(2)$ gebracht, wobei dann jedes Symbol durch m Bit dargestellt wird.
Fassen wir die bisherigen Aussagen kurz zusammen:
$\text{Definition:}$ Ein $(n, k)$–Reed–Solomon–Code für das Galoisfeld ${\rm GF}(2^m)$ wird festgelegt durch
- die $n= 2^{m-1}$ Elemente von ${\rm GF}(2^m) \hspace{-0.05cm}\setminus \hspace{-0.05cm} \{0\} =\{ \alpha^0, \alpha^1, \, \text{...} , \alpha^{n-1}\}$, wobei $\alpha$ ein primitives Element von ${\rm GF}(2^m)$ bezeichnet,
- ein an den Informationsblockt $\underline{u}$ angepasstes Polynom vom Grad $k-1$ der Form
- \[u(x) = \sum_{i = 0}^{k-1} u_i \cdot x^{i} = u_0 + u_1 \cdot x + u_2 \cdot x^2 + \hspace{0.1cm}... \hspace{0.1cm}+ u_{k-1} \cdot x^{k-1} \hspace{0.05cm},\hspace{0.4cm} u_i \in {\rm GF}(2^m) \hspace{0.05cm}.\]
Damit lässt sich der $(n, k)$–Reed–Solomon–Code beschreiben als
- \[C_{\rm RS} = \Big \{ \underline {c} = \big ( u(\alpha^{0}) \hspace{0.05cm},\hspace{0.1cm} u(\alpha^{1})\hspace{0.05cm},\hspace{0.1cm}...\hspace{0.1cm}, u(\alpha^{n-1})\hspace{0.1cm} \big ) \hspace{0.1cm} \big \vert \hspace{0.2cm} u(x) = \sum_{i = 0}^{k-1} u_i \cdot x^{i}\hspace{0.05cm},\hspace{0.2cm} u_i \in {\rm GF}(2^m) \Big \} \hspace{0.05cm}.\]
Die bisherigen Angaben sollen nun an zwei einfachen Beispielen verdeutlicht werden.
$\text{Beispiel 1:}$ Wir betrachten die folgenden Codeparametern:
- \[k = 2 \hspace{0.05cm},\hspace{0.15cm}n = 3 \hspace{0.5cm} \Rightarrow \hspace{0.5cm} \underline {u} = (u_0, u_1)\hspace{0.05cm},\hspace{0.15cm} \underline {c} = (c_0, c_1, c_2)\hspace{0.05cm},\]
- \[q = n+1 = 4 \hspace{0.45cm} \Rightarrow \hspace{0.5cm} {\rm GF} (q) = {\rm GF} (2^m) \hspace{0.5cm} \Rightarrow \hspace{0.5cm} m = 2\hspace{0.05cm}.\]
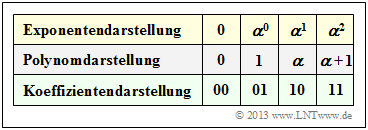
Ausgehend von der Bedingungsgleichung $p(\alpha) = \alpha^2 + \alpha + 1 = 0$ ⇒ $\alpha^2 = \alpha + 1$ erhält man die Zuordnungen zwischen
- der Exponentendarstellung,
- der Polynomdarstellung und
- der Koeffizientendarstellung
von ${\rm GF}(2^2)$ gemäß obiger Tabelle. Daraus ist ersichtlich:
- Der Koeffizientenvektor wird durch das Polynom $u(x) = u_0 + u_1 \cdot x$ ausgedrückt. Der Polynomgrad ist $k- 1 = 1$.
- Für $u_0 = \alpha^1$ und $u_1 = \alpha^2$ erhält man beispielsweise das Polynom $u(x) = \alpha + \alpha^2 \cdot x$ und damit
- \[c_0 = u (x = \alpha^0) = u (x = 1) = \alpha + \alpha^2 \cdot 1 = \alpha + (\alpha + 1) =1 \hspace{0.05cm},\]
- \[c_1 =u (x = \alpha^1) = \alpha + \alpha^2 \cdot \alpha = \alpha + \alpha^3 = \alpha + \alpha^0 = \alpha + 1 = \alpha^2 \hspace{0.05cm},\]
- \[c_2 =u (x = \alpha^2) = \alpha + \alpha^2 \cdot \alpha^2 = \alpha + \alpha^4 = \alpha + \alpha^1 = 0 \hspace{0.05cm}.\]
Daraus ergeben sich folgende Zuordnungen auf Symbol– bzw. Bitebene:
- \[\underline {u} =(\alpha^1, \alpha^2)\hspace{0.57cm}\leftrightarrow\hspace{0.3cm} \underline {c} = (1, \alpha^2, 0)\hspace{0.05cm},\hspace{1cm}\underline {u}_{\rm bin} =(1,0,1,1)\hspace{0.3cm}\leftrightarrow\hspace{0.3cm} \underline {c}_{\rm bin} = (0,1,1,1,0,0)\hspace{0.05cm}.\]
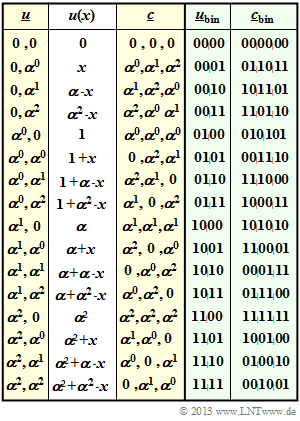
$\text{Beispiel 2:}$ Rechts ist die Codetabelle des RSC (3, 2, 2)4 genannten Reed–Solomon–Codes.
- Die Bezeichnung bezieht sich auf die Parameter $n=3$, $k=2$, $d_{\rm min}=2$ und $q = 4$.
- In den Spalten 1 bis 3 erkennt man den Zusammenhang $\underline {u} \ → \ u(x) \ → \ \underline {c}$.
- In den beiden letzten Spalten ist die Codiervorschrift $\underline {u}_{\rm bin} \ ↔ \ \underline {c}_{\rm bin}$ angegeben.
Zur Verdeutlichung nochmals der Eintrag für $(\alpha^0, \, \alpha^2)$:
- \[u(x) = u_0 + u_1 \cdot x = \alpha^0 + \alpha^2 \cdot x. \]
Daraus ergeben sich folgende Codesymbole:
- \[c_0 = u (x = \alpha^0) = 1 + \alpha^2 \cdot 1 = 1 + (1+\alpha ) =\alpha \hspace{0.05cm},\]
- \[c_1 = u (x = \alpha^1) = 1 + \alpha^2 \cdot \alpha = 1 + (1+\alpha ) \cdot \alpha = 1 + \alpha + \alpha^2 = 0 \hspace{0.05cm},\]
- \[c_2 =u (x = \alpha^2) = 1 + \alpha^2 \cdot \alpha^2 = 1 + \alpha = \alpha^2 \hspace{0.05cm}.\]
Hinweise:
- Aus der Elementenmenge $\{0, \alpha^0 = 1, \alpha^1 = \alpha, \alpha^2\}$ sollte nicht geschlossen werden, dass für diesen Code die 3D–Darstellung mit den Achsen $\alpha^0 = 1$, $\alpha^1 = \alpha$ und $\alpha^2$ zutrifft.
- Aus der Koeffizientendarstellung geht vielmehr eindeutig hervor, dass ${\rm GF} (2^m)$ ein zweidimensionaler Code ist, wobei die Achsen der 2D–Darstellung mit $\alpha^0 = 1$ und $\alpha^1 = \alpha$ zu beschriften sind.
Generatormatrix der Reed–Solomon–Codes
Da es sich beim Reed–Solomon–Code um einen linearen Blockcode handelt, ist der Zusammenhang zwischen Informationswort $\underline {u}$ und Codewort $\underline {c}$ durch die Generatormatrix $\boldsymbol{\rm G}$ gegeben:
\[\underline {c} = \underline {u} \cdot { \boldsymbol{\rm G}} \hspace{0.05cm}.\]
Wie bei jedem linearen $(n, k)$–Blockcode besteht die Generatormatrix aus $k$ Zeilen und $n$ Spalten. Im Gegensatz zum Kapitel Allgemeine Beschreibung linearer Blockcodes sind nun aber die Elemente der Generatormatrix nicht mehr binär ($0$ oder $1$), sondern entstammen dem Galoisfeld ${\rm GF}(2^m) \hspace{-0.05cm}\setminus \hspace{-0.05cm} \{0\} $.
$\text{Beispiel 3:}$ Wir betrachten wie im Beispiel 2 auf der vorherigen Seite wieder den RSC (3, 2, 2)4, dessen Generatormatrix folgende Form hat:
\[ { \boldsymbol{\rm G} } = \begin{pmatrix} g_{00} & g_{01} & g_{02}\\ g_{10} & g_{11} & g_{12} \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} g_{ij} \in {\rm GF}(2^2) \hspace{-0.01cm}\setminus \hspace{-0.01cm} \{0\} = \big \{\hspace{0.05cm} \alpha^{0} \hspace{0.05cm},\hspace{0.1cm} \alpha^{1}\hspace{0.05cm},\hspace{0.1cm} \alpha^{2} \hspace{0.05cm}\big \}\hspace{0.05cm}. \]
Daneben gilt:
- Die erste Zeile von $\boldsymbol{\rm G}$ gibt das Codewort für das Informationswort $\underline {u}_1 = (1, 0)$ an bzw. für die Polynomfunktion $u_1(x) = 1$. Damit erhält man die Matrixelemente der ersten Zeile zu
- \[g_{00} = u_{1}(\alpha^{0}) = 1\hspace{0.05cm},\hspace{0.3cm} g_{01} = u_{1}(\alpha^{1}) = 1\hspace{0.05cm},\hspace{0.3cm} g_{02} = u_{1}(\alpha^{2}) = 1\hspace{0.05cm}.\]
- Die zweite Zeile ist gleich dem Codewort für das Informationswort $\underline {u}_2 = (0, 1)$ ⇒ $u_2(x) = x$. Die Matrixelemente der zweiten Zeile lauten somit:
- \[g_{10} = u_{2}(\alpha^{0}) = \alpha^{0} = 1\hspace{0.05cm},\hspace{0.3cm} g_{11} = u_{2}(\alpha^{1}) = \alpha \hspace{0.05cm},\hspace{0.3cm} g_{12} = u_{2}(\alpha^{2}) = \alpha^{2}\hspace{0.05cm}.\]
- \[\Rightarrow\hspace{0.3cm} { \boldsymbol{\rm G} } = \begin{pmatrix} 1 & 1 & 1\\ 1 & \alpha & \alpha^2 \end{pmatrix}\hspace{0.05cm}.\]
Für das Informationswort $\underline {u}= (u_0, u_1)$ mit den Symbolen $u_0, u_1 ∈ \{0, \alpha^0, \alpha^1 = \alpha, \alpha^2\}$ erhält man unter Berücksichtigung der beiden Gleichungen $\alpha^2 = \alpha + 1$ sowie $\alpha^3 = \alpha^0 = 1$ wiederum die Codetabelle des RSC (3, 2, 2)4 auf Symbolebene.
Man erhält natürlich mit der Generatormatrix genau die gleiche Codetabelle $\underline {u} ↔ \underline {c}$ wie nach der Berechnung über die Funktion $u(x)$. Die entsprechende Codetabelle auf Bitebene (siehe Beispiel 2 auf der vorherigen Seite) ergibt sich wieder, wenn man die Elemente nicht in Exponentendarstellung angibt, sondern in Koeffizientenform:
- \[(0, \hspace{0.1cm}\alpha^{0}, \hspace{0.1cm}\alpha^{1}, \hspace{0.1cm}\alpha^{2}) \hspace{0.3cm}\Leftrightarrow\hspace{0.3cm}(00, \hspace{0.1cm}01, \hspace{0.1cm}10, \hspace{0.1cm}11) \hspace{0.05cm}. \]
Generatormatrix und Prüfmatrix
Wir verallgemeinern nun das Ergebnis der letzten Seite für einen Reed–Solomon–Code mit
- der Dimension $k$ (Symbolanzahl pro Informationsblock),
- der Codewortlänge $n$ (Symbolanzahl pro Codewort).
Die Generatormatrix $\boldsymbol{\rm G}$ (mit $k$ Zeilen und $n$ Spalten) und die Prüfmatrix $\boldsymbol{\rm H}$ ($n-k$ Zeilen, $n$ Spalten) müssen gemeinsam folgende Gleichung erfüllen:
- \[{ \boldsymbol{\rm G}} \cdot { \boldsymbol{\rm H }}^{\rm T}= { \boldsymbol{\rm 0}}\hspace{0.05cm}.\]
Hierbei bezeichnet $\boldsymbol{\rm 0}$ eine Nullmatrix (alle Elemente gleich $0$) mit $k$ Zeilen und $n-k$ Spalten.
$\text{Beispiel 4:}$ Wir betrachten den RSC (7, 3, 5)8 ⇒ Codeparameter $n= 7$, $k= 3$, basierend auf dem Galoisfeld $\rm GF(2^3 = 8)$ mit der Nebenbedingung $\alpha^3 =\alpha + 1$. Beachten Sie hinsichtlich der Codebezeichnung:
- Der dritte Parameter der für Blockcodes üblichen Nomenklatur nennt die freie Distanz $d_{\rm min}= 5$.
- Anders als bei den im Kapitel Beispiele binärer Blockcodes behandelten binären Codes (Single Parity–check Code, Repetition Code, Hamming Code) wird bei den Reed–Solomon–Codes noch der Hinweis $q$ zum Galoisfeld hinzugefügt (hier: $q = 8$).
Alle Elemente der Generatormatrix und der Prüfmatrix
\[{ \boldsymbol{\rm G} } = \begin{pmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5} \end{pmatrix}\hspace{0.05cm},\hspace{0.4cm} { \boldsymbol{\rm H} } = \begin{pmatrix} 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5}\\ 1 & \alpha^3 & \alpha^6 & \alpha^2 & \alpha^{5} & \alpha^{1} & \alpha^{4}\\ 1 & \alpha^4 & \alpha^1 & \alpha^{5} & \alpha^{2} & \alpha^{6} & \alpha^{3} \end{pmatrix} \]
entstammen dem Galoisfeld ${\rm GF}(2^3) \hspace{-0.01cm}\setminus \hspace{-0.01cm} \{0\} = \big \{\hspace{0.05cm} \alpha^{0} \hspace{0.05cm},\hspace{0.1cm}\alpha^{1}\hspace{0.05cm},\hspace{0.1cm} \alpha^{2} \hspace{0.05cm} \alpha^{3} \hspace{0.05cm},\hspace{0.1cm}\alpha^{4}\hspace{0.05cm},\hspace{0.1cm} \alpha^{5} \hspace{0.05cm},\hspace{0.1cm} \alpha^{6} \hspace{0.05cm}\big \}$. Für das Matrixprodukt gilt:
- \[{ \boldsymbol{\rm G} } \cdot { \boldsymbol{\rm H } }^{\rm T}= \begin{pmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5} \end{pmatrix} \begin{pmatrix} 1 & 1 & 1 & 1 \\ \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4\\ \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1\\ \alpha^3 & \alpha^6 & \alpha^2 & \alpha^{5}\\ \alpha^4 & \alpha^1 & \alpha^{5} & \alpha^{2}\\ \alpha^5 & \alpha^{3} & \alpha^{1} & \alpha^{6}\\ \alpha^6 & \alpha^{5} & \alpha^{4} & \alpha^{3} \end{pmatrix} = \begin{pmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} \hspace{0.05cm}.\]
Dies soll hier nur für zwei Elemente nachgewiesen werden:
- Erste Zeile, erste Spalte:
- \[1 \hspace{0.1cm} \cdot \hspace{0.1cm} \big [1 + \alpha^1 + \alpha^2 + \alpha^3 + \alpha^4 + \alpha^5 + \alpha^6 \big ] = 1 + \alpha + \alpha^2 + (\alpha + 1) + (\alpha^2 + \alpha)+ (\alpha^2 + \alpha +1)+ (\alpha^2 + 1) = 0 \hspace{0.05cm}; \]
- Letzte Zeile, letzte Spalte:
- \[1 \hspace{0.1cm} \cdot \hspace{0.1cm} 1 + \alpha^2 \cdot \alpha^4 + \alpha^4 \cdot \alpha^1 + \alpha^6 \cdot \alpha^5+ \alpha^1 \cdot \alpha^2+ \alpha^3 \cdot \alpha^6+ \alpha^5 \cdot \alpha^3= 1 + \alpha^6 + \alpha^5 + \alpha^{11} + \alpha^{3}+ \alpha^{9}+ \alpha^{8} =\]
- \[ \hspace{1.5cm} = \hspace{0.15cm} 1 + \alpha^6 + \alpha^5 + \alpha^{4} + \alpha^{3}+ \alpha^{2}+ \alpha^{1} =0 \hspace{0.05cm}.\]
Singleton–Schranke und minimale Distanz
Eine wichtige Kenngröße eines jeden Blockcodes ist die minimale Distanz zwischen zwei beliebigen Codeworten $\underline {c}_i$ und $\underline {c}_j$.
- Die Reed–Solomon–Codes gehören zur Klasse der linearen und zyklischen Codes. Bei diesen kann man vom Nullwort $\underline {c}_0 = (0, 0, \hspace{0.05cm} \text{...} \hspace{0.05cm}, 0)$ als Bezugsgröße ausgehen.
- Aus der Anzahl der Nullen in den anderen Codeworten $\underline {c}_j ≠ \underline {c}_0$ lässt sich das Distanzspektrum $\{ \hspace{0.05cm}W_j\hspace{0.05cm}\}$ angeben.
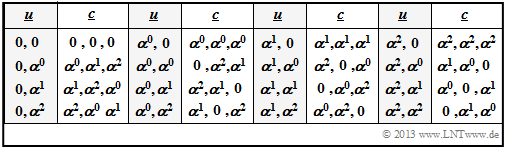
$\text{Beispiel 5:}$ Die Tabelle verdeutlicht die Bestimmung des Distanzspektrums für den RSC (3, 2, 2)4.
- Gegenüber den bisherigen Grafiken wird die Symbolmenge vereinfachend mit $\{0, 1, 2, 3\}$ anstelle von $\{0, \alpha^0, \alpha^1, \alpha^2\}$ bezeichnet.
- Die Distanz $d$ zwischen $\underline {c}_j$ und dem Nullwort &$\underline {c}_0$ ist identisch dem Hamming–Gewicht $w_{\rm H}(\underline {c}_j)$.
Aus der oberen Tabelle kann unter anderem abgelesen werden:
- Neun der Codeworte unterscheiden sich vom Nullwort in zwei Symbolen und sechs Codeworte in drei Symbolen: $W_2 = 9$, $W_3 = 6$.
- Es gibt kein einziges Codewort mit nur einer Null. Das heißt: Die minimale Distanz beträgt hier $d_{\rm min} = 2$.
Aus der unteren Tabelle erkennt man, dass auch für die Binärdarstellung $d_{\rm min} = 2$ gilt.
Dieses empirische Ergebnis soll nun verallgemeinert werden:
$\text{Ohne Beweis:}$
- Die minimale Distanz eines jeden $(n, k)$–Reed–Solomon–Codes beträgt $d_{\rm min} =n-k+1$. Damit lassen sich $e = d_{\rm min} -1 =n-k$ Symbolfehler erkennen.
- Bei fehlerkorrigierenden Codes wählt man meist ein $d_{\rm min} $ ungeradzahlig ⇒ $n-k$ geradzahlig. Bei RS–Codes können dann bis zu $t =(n-k)/2$ Symbolfehler korrigiert werden.
- Die Singleton–Schranke besagt, dass für alle linearen Codes $d_{\rm min} \le n-k+1$ gilt. RS–Codes erreichen diese Schranke mit Gleichheit; sie sind so genannte MDS–Codes (Maximum Distance Separable).
- Das Distanzspektrum setzt sich zusammen aus $W_0 = 1$ sowie weiteren Gewichtsfaktoren $W_i$ mit $d ≤ i ≤ n$, wobei in der folgenden Gleichung $d_{\rm min}$ mit $d$ abgekürzt ist:
- \[W_i = {n \choose i} \cdot \sum_{j = 0}^{i-d}\hspace{0.15cm}(-1)^j \cdot {i \choose j} \cdot \bigg [\hspace{0.03cm}q^{i\hspace{0.03cm}-\hspace{0.03cm}j\hspace{0.03cm}-\hspace{0.03cm}d\hspace{0.03cm}+\hspace{0.03cm}1}-1 \hspace{0.03cm} \bigg ]\hspace{0.05cm}.\]
Codebezeichnung und Coderate
Die übliche Bezeichnung für die Reed–Solomon–Codes ist RSC (n, k, dmin)q mit
- der Länge n des Codes (Symbolanzahl eines Codewortes),
- der Dimension k des Codes (Symbolanzahl eines Informationswortes),
- der minimalen Distanz dmin = n – k + 1, maximal entsprechend der Singleton–Schranke, und
- der Größe q = 2m des Galoisfeldes ⇒ GF(q).
Alle Elemente ui des Informationswortes u = (u0, ..., ui, ..., uk–1) und alle Elemente ci des Codewortes c = (c0, ..., ci, ..., cn–1) sind nicht binäre Symbole und entstammen dem Galoisfeld GF(q).
Für die Realisierung werden diese Symbole stets auch binär dargestellt ⇒ ui, xi ∈ GF(2), und man kommt zum äquivalenten binären Code RSC (nbin, kbin, dmin)2 mit
- nbin = n · m Bit eines Codewortes,
- kbin = k · m Bit eines Informationswortes.
Die Coderate wird durch diese Maßnahme nicht verändert:
\[R = \frac{k}{n}= \frac{k_{\rm bin}}{n_{\rm bin}} = \frac{k \cdot m}{n \cdot m} = \frac{k}{n} \hspace{0.05cm}.\]
Ebenso ändert sich durch den Übergang von GF(q) auf GF(2) nichts an der minimalen Distanz dmin.
\[W_0 = 1\hspace{0.05cm}, \hspace{0.2cm}W_2 = 9\hspace{0.05cm}, \hspace{0.2cm}W_3 = 6\hspace{0.3cm}\Rightarrow\hspace{0.3cm}W(X) = 1 + 9 \cdot X^2 + 6 \cdot X^3\hspace{0.05cm}.\]
Die binäre Repräsentation des Codes RSC (3, 2, 2)4 führt zum RSC (6, 4, 2)2, ebenfalls mit der Rate R = 4/6 = 2/3 und der Minimaldistanz dmin = 2. Es ergibt sich allerdings ein anderes Distanzspektrum:
\[W_0 = 1\hspace{0.05cm}, \hspace{0.2cm}W_2 = 3\hspace{0.05cm}, \hspace{0.2cm}W_3 = 8 \hspace{0.05cm}, \hspace{0.2cm}W_4 = 3\hspace{0.05cm}, \hspace{0.2cm}W_6 = 1\]
\[\Rightarrow\hspace{0.3cm}W(X) = 1 + 3 \cdot X^2 + 8 \cdot X^3 + 4 \cdot X^4 + X^6 \hspace{0.05cm}.\]
Bedeutung der Reed–Solomon–Codes
Anhand des hier oft beispielhaft betrachteten RSC (3, 2, 2)4 konnten wir viele Eigenschaften der Reed–Solomon–Codes in überschaubarem Rahmen kennenlernen. Praxisrelevant ist dieser Code nicht, da wegen dmin = 2 kein einziger Fehler korrigiert und auch nur ein einziger Fehler erkannt werden kann. Schon der nächstgrößere Code RSC (7, 3, 5)8, der bis zu t = 2 Fehler korrigieren kann, weist bereits eine Codetabelle mit 83 = 512 Einträgen auf und ist zu Demonstrationszwecken weniger gut geeignet.
In der Praxis werden meist größere RS–Codes eingesetzt, zum Beispiel der RSC (255, 223, 33)256 mit den folgenden Eigenschaften:
- Der Code basiert auf dem Galoisfeld GF(28). Jedes Symbol entspricht somit einem Byte. Die Coderate ist mit R = 0.8745 relativ groß.
- Trotz dieser großen Coderate (geringen Redundanz) können mit diesem Code bis zu e = 32 Fehler innerhalb eines Blocks aus 255 Symbolen erkannt und t = 16 Fehler korrigiert werden.
- Die Codetabelle würde allerdings 28 · 223 = 21784 ≈ 10537 Einträge aufweisen und wird deshalb wahrscheinlich auch von niemanden tatsächlich erstellt.
Der große Vorteil der Reed–Solomon–Codes (und einer ganzen Reihe davon abgeleiteter weiterer Codes) ist zum einen, dass sie analytisch geschlossen konstruiert werden können, zum anderen ihre große Flexibilität hinsichtlich der Codeparameter. Meist geht man wie folgt vor:
- Man gibt die Korrekturfähigkeit in Form des Parameters t vor. Daraus ergibt sich die minimale Distanz dmin = 2t + 1 und die Differenz n – k = 2t entsprechend der Singleton–Schranke. Einen besseren Wert gibt es nicht.
- Ein weiterer Entwurfsparameter ist die Coderate R = k/n, wobei die Codewortlänge n = 2m – 1 nicht völlig frei wählbar ist. Durch Erweiterung, Verkürzung und Punktierung – siehe Aufgabe Z1.9 – kann die Vielzahl an möglichen Codes weiter vergrößert werden.
- Bei Reed–Solomon–Codes ist die Gewichtsverteilung exakt bekannt und es ist eine Anpassung an die Fehlerstruktur des Kanals möglich. Sie sind insbesondere für Bündelfehlerkanäle gut geeignet, die bei mobilen Funksystemen aufgrund von temporären Abschattungen häufig vorliegen.
- Im Falle statistisch unabhängiger Fehler sind BCH–Codes (von Bose–Chaudhuri–Hocquenghem) besser geeignet. Diese sind eng verwandt mit den RS–Codes, allerdings erfüllen sie nicht immer das Singleton–Kriterium. Eine ausführliche Beschreibung finden Sie in [Fri96][1].
- Die Decodierung nach dem BDD–Prinzip (Bounded Distance Decoding) kann rechentechnisch sehr einfach erfolgen, zum Beispiel mit dem Berlekamp–Massey–Algorithmus. Zudem kann im Decoder ohne wesentlichen Mehraufwand auch Soft–Decision–Information verarbeitet werden.
Aufgaben
A2.7 Reed–Solomon–Code (7, 3, 5)(Base 8)
Zusatzaufgaben:2.7 Reed–Solomon–Code (15, 5, 11)(Base 16)
Zusatzaufgaben:2.8 „Plus” und „Mal” in GF(2^3)
Zusatzaufgaben:2.10 Coderate und minimale Distanz
Quellenverzeichnis
- ↑ Friedrichs, B.: Kanalcodierung – Grundlagen und Anwendungen in modernen Kommunikations- systemen. Berlin – Heidelberg: Springer, 1996.