Aufgaben:Exercise 1.4: AMI and MMS43 Code

• Return to book

Modifizierter AMI- und MMS43-Code

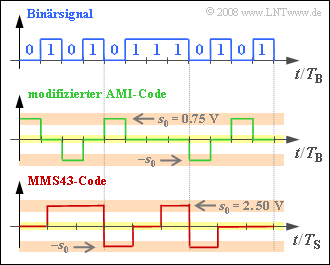
Bei ISDN werden zwei verschiedene ternäre Übertragungscodes eingesetzt, die in der Grafik an einem beispielhaften binären Eingangssignal verdeutlicht werden sollen. Im oberen Diagramm sind $12 \ \rm Bit$ (jeweils mit der Bitdauer $T_{\rm B}$) dargestellt.

• Auf der $S_{0}$–Schnittstelle (zwischen NTBA und Endgerät) verwendet man wird den modifizierten AMI–Code. Der Unterschied zum herkömmlichen AMI–Code ist die Vertauschung $0 \Leftrightarrow 1$ des binären Eingangssignals.
• Dagegen wird auf der $U_{K0}$–Schnittstelle der MMS43–Code (Modified Monitoring Sum 4B3T) eingesetzt, wobei jeweils $4$ Binärsymbole durch $3$ Ternärsymbole (Spannungswerte $0 \ {\rm V}, +2.5 \ {\rm V}$ und $–2.5 \ {\rm V}$) ersetzt werden. Die Zuordnung erfolgt abhängig von den vorher codierten Symbolen.

Hinweis:

Die Aufgabe behandelt das Themengebiet von ISDN-Basisanschluss des vorliegenden Buches. Angaben zum MMS43–Code finden Sie im Blockweise Codierung mit 4B3T-Codes des Buches „Digitalsignalübertragung” und zum AMI–Code im Symbolweise Codierung mit Pseudoternärcodes des gleichen Buches.

Fragebogen

1

Welche Eigenschaften weist der modifizierte AMI–Code auf?

	Symboldauer $T_{\rm S}$ und Bitdauer $T_{\rm B}$ des Binärsignals sind gleich.
	Die Codierung geschieht symbolweise.
	Jede binäre „$0$” wird durch „$0 \ \rm V$” dargestellt.
	Die binäre „$1$” wird alternierend mit $+s_{0}$ und $–s_{0}$ repräsentiert.

2

Wie groß ist die Redundanz des (modifizierten) AMI–Codes?

$r_{\rm AMI} \ = \ $ $\ \%$

3

Es gelte $s_{0} = 0.75 \ {\rm V}, R = 100 \ {\rm Ω}$. Wie groß ist die mittlere Sendeleistung?

$P_{\rm S, \ AMI} \ = \ $ $\ \rm mW$

4

Welche Eigenschaften zeigt der MMS43–Code?

	Symboldauer $T_{\rm S}$ und Bitdauer $T_{\rm B}$ des Binärsignals sind gleich.
	Die Codierung erfolgt blockweise.
	Jede binäre „$0$” wird durch „$0 \ \rm V$” dargestellt.

5

Wie groß ist die Redundanz des MMS43–Codes?

$r_{\rm MMS43} \ = \ $ $\ \%$

6

Wie groß ist die Symbolrate auf dem $U_{\rm K0}$–Bus, wenn pro Millisekunde $12$ ternäre Synchronisations– und Steuersymbole zu berücksichtigen sind?

$R_{\rm UK0} \ = \ $ $\ \rm Ternärsymbole/Sekunde$

7

Es gelte $s_{0} = 2.5 \ {\rm V}, R = 100 \ {\rm \Omega }$. Wie groß ist die Sendeleistung? Hinweis: Gehen Sie von gleichwahrscheinlichen Ternärsymbolen aus.

$P_{\rm S,\ MMS43} \ = \ $ $\ \rm mW$

Musterlösung

Solution

(1)  (2)  (3)  (4)  (5)  (6)  (7)