Aufgaben:Exercise 3.4: Systematic Convolution Codes

• Return to book

Vorgegebene Filterstrukturen

Man spricht von einem systematischen Faltungscode der Rate $R = 1/2$  ⇒  $k = 1, \ n = 2$, wenn das Codebit $x_i^{(1)}$ gleich dem momentan anliegenden Informationsbit $u_i$ ist.

Die Übertragungsfunktionsmatrix eines solchen Codes lautet:

$${\boldsymbol{\rm G}}(D) = \big ( \hspace{0.05cm} 1\hspace{0.05cm} , \hspace{0.2cm} G^{(2)}(D) \hspace{0.05cm}\big ) \hspace{0.05cm}.$$

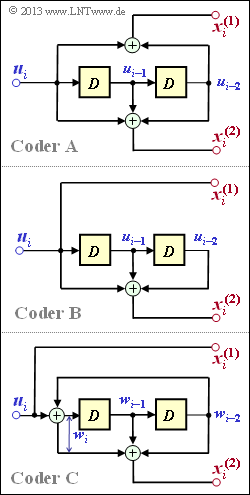
Der in der oberen Grafik dargestellte Coder A ist sicher nicht systematisch, da für diesen $G^{(1)}(D) ≠ 1$ gilt. Zur Herleitung der Matrix $\mathbf{G}(D)$ verweisen wir auf ein früheres Beispiel, in dem für unseren Standard–Rate–1/2–Coder mit Gedächtnis $m = 2$ ermittelt wurde:

$${\boldsymbol{\rm G}}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \big ( \hspace{0.05cm} G^{(1)}(D)\hspace{0.05cm} , \hspace{0.2cm} G^{(2)}(D) \hspace{0.05cm}\big ) =$$

$$ \ = \ \hspace{-0.15cm} \big ( \hspace{0.05cm} 1 + D + D^2\hspace{0.05cm} , \hspace{0.2cm} 1 + D^2 \hspace{0.05cm}\big ) \hspace{0.05cm}.$$

Der Coder A unterscheidet sich gegenüber diesem Beispiel nur durch Vertauschen der beiden Ausgänge. Lautet die Übertragungsfunktionsmatrix eines Codes

$${\boldsymbol{\rm G}}(D) = \big ( \hspace{0.05cm} G^{(1)}(D)\hspace{0.05cm} , \hspace{0.2cm} G^{(2)}(D) \hspace{0.05cm}\big ) \hspace{0.05cm},$$

so gilt für die äquivalente systematische Repräsentation dieses Rate–1/2–Faltungscodes allgemein:

$${\boldsymbol{\rm G}}_{\rm sys}(D) = \big ( \hspace{0.05cm} 1\hspace{0.05cm} , \hspace{0.2cm} {G^{(2)}(D)}/{G^{(1)}(D)} \hspace{0.05cm}\big ) \hspace{0.05cm}.$$

In der Teilaufgabe (3) ist zu prüfen, welcher der systematischen Anordnungen (entweder Code B oder Code C oder auch beide) äquivalent zum Code A ist.

Hinweis:

• Die Aufgabe bezieht sich auf die Thematik von Kapitel 3.2.

Fragebogen

1

Wie lautet die Übertragungsfunktionsmatrix von Coder A?

	$\mathbf{G}(D) = (1 + D^2, \ 1 + D + D^2)$,
	$\mathbf{G}(D) = (1 + D + D^2, \ 1 + D^2)$,
	$\mathbf{G}(D) = (1, \ 1 + D + D^2)$.

2

Wie lautet die äquivalente systematische Übertragungsfunktionsmatrix?

	$\mathbf{G}_{\rm sys}(D) = (1 + D + D^2, \ 1 + D^2)$,
	$\mathbf{G}_{\rm sys}(D) = (1, \ 1 + D + D^2)$,
	$\mathbf{G}_{\rm sys}(D) = (1, \ (1 + D + D^2)/(1 + D^2))$.

3

Welcher Coder ist zu Coder A äquivalent und systematisch?

	Coder B,
	Coder C.

Musterlösung

Solution

(1)  Richtig ist der Lösungsvorschlag 1. Der Vorschlag 2 würde sich ergeben, wenn man die beiden Ausgänge vertauscht, also für den im Theorieteil meist betrachteten Rate–1/2–Standardcode.

Der Vorschlag 3 gilt für einen systematischen Code ⇒ $\underline{x}^{(1)} = \underline{u}$. Der hier betrachtete Coder A weist diese Eigenschaft allerdings nicht auf.

(2)  Um von einem nichtsystematischen $(n, \ k)$–Code mit Matrix $\mathbf{G}(D)$ zum äquivalenten systematischen Code ⇒ Matrix $\mathbf{G}_{\rm sys}(D)$ zu gelangen, muss man allgemein $\mathbf{G}(D)$ aufspalten in eine $k × k$–Matrix $\mathbf{T}(D)$ und eine Restmatrix $\mathbf{Q}(D)$. Das gewünschte Ergebnis lautet dann mit der $k × k$–Einheitsmatrix $\mathbf{I}_k$:

$${\boldsymbol{\rm G}}_{\rm sys}(D) = \big ( \hspace{0.05cm} {\boldsymbol{\rm I}}_k\hspace{0.05cm} ; \hspace{0.1cm} {\boldsymbol{\rm T}}^{-1}(D) \cdot {\boldsymbol{\rm Q}}(D)\hspace{0.05cm}\big ) \hspace{0.05cm}.$$

Wir gehen hier von der $\mathbf{G}(D)$–Matrix für den Coder A aus. Wegen $k = 1$ haben hier sowohl $\mathbf{T}(D)$ als auch $\mathbf{Q}(D)$ die Dimension $1 × 1$, sind also streng genommen gar keine Matrizen:

$${\boldsymbol{\rm G}}(D) = \big ( \hspace{0.05cm} {\boldsymbol{\rm T}}(D)\hspace{0.05cm} ; \hspace{0.2cm} {\boldsymbol{\rm Q}}(D)\hspace{0.05cm}\big ) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\boldsymbol{\rm T}}(D) = \big ( 1+D^2\big )\hspace{0.05cm} , \hspace{0.2cm} {\boldsymbol{\rm Q}}(D) = \big ( 1+D+D^2\big )\hspace{0.05cm} .$$

Für die beiden Elemente der systematischen Übertragungsfunktionsmatrix erhält man:

$$G^{(1)}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\boldsymbol{\rm T}}(D) \cdot {\boldsymbol{\rm T}}^{-1}(D) = 1 \hspace{0.05cm},$$

$$G^{(2)}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\boldsymbol{\rm Q}}(D) \cdot {\boldsymbol{\rm T}}^{-1}(D) = \frac{1+D+D^2}{1+D^2}$$

$$\Rightarrow \hspace{0.3cm}{\boldsymbol{\rm G}}_{\rm sys}(D) = \big ( \hspace{0.05cm} 1\hspace{0.05cm} , \hspace{0.1cm} \frac{1+D+D^2}{1+D^2} \hspace{0.05cm}\big ) \hspace{0.05cm}.$$

Richtig ist also der letzte Lösungsvorschlag. Der Lösungsvorschlag 1 beschreibt keinen systematischen Code. Ein Code entsprechend Lösungsvorschlag 2 ist zwar systematisch, aber nicht äquivalent zum Code A entsprechend der vorgegebenen Schaltung und Übertragungsfunktionsmatrix $\mathbf{G}(D)$.

(3)  Die Generatorfunktionsmatrix von Coder B lautet:

$${\boldsymbol{\rm G}}_{\rm B}(D) = \big ( \hspace{0.05cm} 1\hspace{0.05cm} , \hspace{0.2cm} {1+D+D^2} \hspace{0.05cm}\big ) \hspace{0.05cm}.$$

Dieser Coder ist also nicht äquivalent zum Coder A. Betrachten wir nun den Coder C. Hier gilt für das zweite Matrixelement von $\mathbf{G}(D)$:

$$w_i \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_i + w_{i-2} \hspace{0.25cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.25cm} {U}(D) = W(D) \cdot (1 + D^2 ) \hspace{0.05cm},$$

$$x_i^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} w_i + w_{i-1} + w_{i-2} \hspace{0.25cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.25cm} {X}^{(2)}(D) = W(D) \cdot (1 +D + D^2 )$$

$$\Rightarrow \hspace{0.3cm} G^{(2)}(D) = \frac{{X}^{(2)}(D)}{{U}(D)} = \frac{1+D+D^2}{1+D^2}\hspace{0.05cm}.$$

Dies entspricht genau dem Ergebnis der Teilaufgabe (2)  ⇒  Lösungsvorschlag 2.