Aufgaben:Exercise 3.7Z: Which Code is Catastrophic?

• Return to book

Codierer und Zustandsübergangsdiagramm für $m = 3$

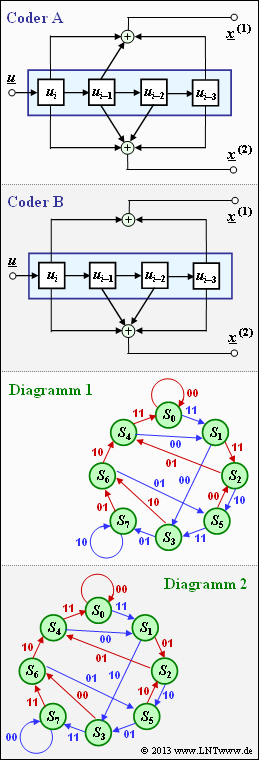
Die nebenstehende Grafik zeigt

• zwei unterschiedliche Coder A und Coder B, jeweils mit dem Gedächtnis $m = 3$ (oben),
• zwei Zustandsübergangsdiagramme, bezeichnet mit Diagramm 1 und Diagramm 2 (unten).

In der letzten Teilaufgabe sollen Sie entscheiden, welches Diagramm zum Coder A gehört und welches zum Coder B.

Zunächst werden die drei Übertragungsfunktionen

• $G(D) = 1 + D + D^2 + D^3$,
• $G(D) = 1 + D^3$, und
• $G(D) = 1 + D + D^3$

analysiert und anschließend die Ausgangssequenzen $\underline{x}$ unter der Voraussetzung

$$\underline{u}= \underline{1}= (1, 1, 1, ... \hspace{0.1cm}) \hspace{0.15cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.15cm} U(D)= \frac{1}{1+D}$$

berechnet. Diese Übertragungsfunktionen stehen im direkten Zusammenhang mit den skizzierten Codierern.

Desweiteren ist noch zu klären, welcher der beiden Codes katastrophal ist. Von einem solchen spricht man, wenn eine endliche Anzahl von Übertragungsfehlern zu unendlich vielen Decodierfehlern führt.

Hinweise:

• Die Aufgabe gehört zum Kapitel Codebeschreibung mit Zustands– und Trellisdiagramm-
• Angegeben werden noch zwei Polynomprodukte in ${\rm GF}(2)$:

$$(1+D) \cdot (1+D^2) \hspace{-0.25cm} \ = \ \hspace{-0.25cm}1+D +D^2+D^3\hspace{0.05cm},$$

$$(1+D) \cdot (1+D+D^2) \hspace{-0.25cm} \ = \ \hspace{-0.25cm}1+D^3\hspace{0.05cm}.$$

Fragebogen

1

Welche Ausgangssequenz $\underline{x}$ ergibt sich für $\underline{u} = \underline{1}, \ G(D) = 1 + D + D^2 + D^3$?

	$\underline{x} = (1, \, 0, \, 0, \, 1, \, 1, \, 1, \, ...)$,
	$\underline{x} = (1, \, 0, \, 1, \, 0, \, 0, \, 0, \, ...)$,
	$\underline{x} = (1, \, 1, \, 1, \, 0, \, 0, \, 0, \, ...)$.
	Die Ausgangsfolge $\underline{x}$ ist zeitlich begrenzt.

2

Welche Ausgangssequenz $\underline{x}$ ergibt sich für $\underline{u} = \underline{1}$ und $G(D) = 1 + D^3$?

	$\underline{x} = (1, \, 0, \, 0, \, 1, \, 1, \, 1, \, ...)$,
	$\underline{x} = (1, \, 0, \, 1, \, 0, \, 0, \, 0, \, ...)$,
	$\underline{x} = (1, \, 1, \, 1, \, 0, \, 0, \, 0, \, ...)$,
	Die Ausgangsfolge $\underline{x}$ ist zeitlich begrenzt.

3

Welche Ausgangssequenz $\underline{x}$ ergibt sich für $\underline{u} = \underline{1}$ und $G(D) = 1 + D + D^3$?

	$\underline{x} = (1, \, 0, \, 0, \, 1, \, 1, \, 1, \, ...)$,
	$\underline{x} = (1, \, 0, \, 1, \, 0, \, 0, \, 0, \, ...)$,
	$\underline{x} = (1, \, 1, \, 1, \, 0, \, 0, \, 0, \, ...)$,
	Die Ausgangsfolge $\underline{x}$ ist zeitlich begrenzt.

4

Wie lautet die Codesequenz $\underline{x}$ von Coder A für die Eins–Sequenz am Eingang?

	$\underline{x} = (11, \, 00, \, 01, \, 10, \, 10, \, 10, \, ...)$,
	$\underline{x} = (11, \, 10, \, 11, \, 00, \, 00, \, 00, \, ...)$,
	$\underline{x} = (11, \, 11, \, 11, \, 11, \, 11, \, 11, \, ...)$.
	Die Codesequenz $\underline{x}$ beinhaltet endlich viele Einsen.

5

Wie lautet die Codesequenz $\underline{x}$ von Coder B für die Eins–Sequenz am Eingang?

	$\underline{x} = (11, \, 00, \, 01, \, 10, \, 10, \, 10, \, ...)$,
	$\underline{x} = (11, \, 10, \, 11, \, 00, \, 00, \, 00, \, ...)$,
	$\underline{x} = (11, \, 11, \, 11, \, 11, \, 11, \, 11, \, ...)$.
	Die Codesequenz $\underline{x}$ beinhaltet endlich viele Einsen.

6

Welche Aussagen treffen für Coder B zu?

	Zu Coder B gehört das Zustandsübergangsdiagramm 1.
	Zu Coder B gehört das Zustandsübergangsdiagramm 2.
	Der Coder B ist katastrophal.

Musterlösung

Solution

(1)  (2)  (3)  (4)  (5)