Difference between revisions of "Aufgaben:Exercise 3.09: Basics of the Viterbi Algorithm"
From LNTwww
| Line 15: | Line 15: | ||
| − | '' | + | ''Hinweise:'' |
* Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Decodierung_von_Faltungscodes| Decodierung von Faltungscodes]]. | * Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Decodierung_von_Faltungscodes| Decodierung von Faltungscodes]]. | ||
| + | * Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| Line 22: | Line 23: | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Welche der folgenden Aussagen werden durch das Trellis bestätigt? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + Es handelt sich um einen Rate–1/2–Faltungscode. |
| − | - | + | - Das Gedächtnis des Codes ist $m = 2$. |
| + | + Der Faltungscode ist terminiert. | ||
| + | - Die Länge der Informationssequenz ist $L = 5$. | ||
| − | { | + | {Geben Sie die freie Distanz $d_{\rm F}$ des Faltungscodes an. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $d_{\rm F} \ = \ ${ 3 3% } |
| + | |||
| + | {Welche Aussagen erlaubt der Endwert ${\it \Gamma}_5(S_0) = 0$ der Fehlergröße? | ||
| + | |type="[]"} | ||
| + | - Es ist kein Übertragungsfehler aufgetreten. | ||
| + | - Das Decodierergebnis $\underline{\nu}$ ist mit Sicherheit richtig (gleich $\underline{u}$). | ||
| + | + Das Decodierergebnis minimiert die Wahrscheinlichkeit ${\rm Pr}(\underline{\nu} ≠ \underline{u}$). | ||
| + | |||
| + | {Welche Aussagen treffen <u>bei einem einzigen</u> Übertragungsfehler zu? | ||
| + | |type="[]"} | ||
| + | + Der Fehlergrößenendwert ist ${\it \Gamma}_5(S_0) = 1$. | ||
| + | + Das Decodierergebnis $\underline{\nu}$ ist mit Sicherheit richtig (gleich $\underline{u}$). | ||
| + | + Das Decodierergebnis minimiert die Wahrscheinlichkeit ${\rm Pr}(\underline{\nu} ≠ \underline{u}$). | ||
| + | |||
| + | {Welche Aussagen treffen <u>bei zwei</u> Übertragungsfehlern zu? | ||
| + | |type="[]"} | ||
| + | - Der Fehlergrößenendwert ist ${\it \Gamma}_5(S_0) = 2$. | ||
| + | - Das Decodierergebnis $\underline{\nu}$ ist mit Sicherheit richtig (gleich $\underline{u}$). | ||
| + | - Das Decodierergebnis $\underline{\nu}$ ist mit Sicherheit falsch (ungleich $\underline{u}$). | ||
</quiz> | </quiz> | ||
Revision as of 21:03, 3 December 2017
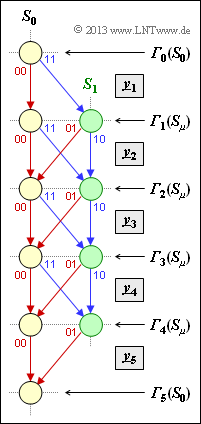
Die Grafik zeigt ein Trellisdiagramm und definiert gleichzeitig die Fehlergrößen ${\it \Gamma}_i(S_0)$ und ${\it \Gamma}_i(S_1)$ zu den Zeitpunkten $i = 0$ bis $i = 5$. Aus diesem Trellis können zum Beispiel abgelesen werden:
- die Coderate $R$,
- das Gedächtnis $m$,
- die freie Distanz $d_{\rm F}$,
- die Informationssequenzlänge $L$,
- die Sequenzlänge $L'$ inklusive der Terminierung.
In der Aufgabe ist weiter zu klären:
- die Bedeutung des Endwertes ${\it \Gamma}_5(S_0)$,
- Auswirkungen von einem bzw. zwei Übertragungsfehlern.
Hinweise:
- Die Aufgabe gehört zum Kapitel Decodierung von Faltungscodes.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)