Mobile Communications/Multi-Path Reception in Mobile Communications

1. Mobile Communications
2. Frequenzselektive Übertragungskanäle
3. Multi-Path Reception in Mobile Communications

• Previous page
• Next page

• Previous page
• Next page

Zeitinvariante Beschreibung des Zweiwegekanals

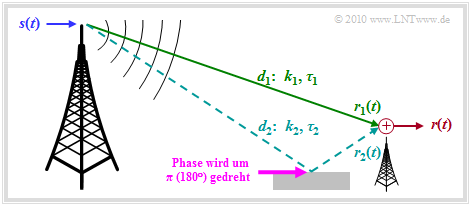
Wir gehen von dem in der Grafik dargestellten Szenario aus. Dabei wird vorausgesetzt:

Zeitinvariante Betrachtung des Zweiwegekanals

• Sender und Empfänger sind ruhend. Dann ist sowohl die Kanal–Übertragungsfunktion als auch die Impulsantwort zeitunabhängig. Für alle Zeiten $t$ gilt $H(f, \hspace{0.05cm}t) = H(f)$ und $h(\tau, \hspace{0.05cm}t) = h(\tau)$.
  

• Ein Zweiwegekanal: Das Sendesignal $s(t)$ erreicht den Empfänger auf direktem Pfad mit der Weglänge $d_1$ und es gibt ein Echo aufgrund des reflektierenden Erdbodens (Distanz $d_2$).

Hinweis: Die hier behandelte Thematik ist Gegenstand des Applets Auswirkungen von Mehrwegeempfang .

Somit gilt für das Empfangssignal:

\[r(t) = r_1(t) + r_2(t) = k_1 \cdot s( t - \tau_1) + k_2 \cdot s( t - \tau_2) \hspace{0.05cm},\]

wobei die folgenden Aussagen zu beachten sind:

• Das über den Direktpfad empfangene Signal $r_1(t)$ ist gegenüber dem Sendesignal $s(t)$ um den Faktor $k_1$ gedämpft und um die Laufzeit $\tau_1$ verzögert.
  

• Der Dämpfungsfaktor $k_1$ wird mit dem Pfadverlustmodell berechnet. $k_1$ ist um so kleiner und somit der Verlust um so größer, je größer die Sendefrequenz $f_{\rm S}$, die Distanz $d_1$ und der Exponent $\gamma$ sind.
  

• Die Laufzeit $\tau_1 = d_1/c$ nimmt proportional mit der Wegelänge $d_1$ zu. Beispielsweise ergibt sich für die Distanz $d_1 = 3 \ \rm km$ mit der Lichtgeschwindigkeit $c = 3 \cdot 10^8 \ \rm m/s$ die Verzögerung $\tau_1 = 10 \ \rm \mu s$.
  

• Wegen der größeren Weglänge $(d_2 > d_1)$ weist der zweite Pfad eine größere Dämpfung auf   ⇒   kleinerer Vorfaktor   ⇒   $(|k_2| < |k_1|)$ und dementsprechend auch eine größere Laufzeit $(\tau_2 > \tau_1)$.
  

• Außerdem ist zu berücksichtigen, dass die Reflexion an Gebäuden oder dem Erdboden zu einer Phasendrehung um $\pi \ (180^\circ)$ führt. Damit wird der Faktor $k_2$ negativ. Im Folgenden wird allerdings das negative Vorzeichen von $k_2$ außer Acht gelassen.
  
  

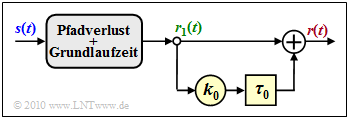
Einfaches zeitinvariantes Modell des Zweiwegekanals

Für die Frequenzselektivität haben Pfadverlust (gekennzeichnet durch $k_1$) und Grundlaufzeit $\tau_1$ keine Bedeutung. Entscheidend sind hier Pfaddverlustunterschiede und Laufzeitdifferenzen.

Ersatzmodell für den Zweiwegekanal

Wir beschreiben nun den Zweiwegekanal mit den neuen Kenngrößen $k_0 = |k_2 /k_1 |$ und $\tau_0 = \tau_2 - \tau_1$ wie folgt:

\[r(t) = r_1(t) + k_0 \cdot r_1( t - \tau_0) \hspace{0.5cm}{\rm mit} \hspace{0.5cm} r_1(t) = k_1 \cdot s( t - \tau_1)\hspace{0.05cm}.\]

Die Grafik veranschaulicht die Gleichung.

Mit den weiteren Vereinfachungen $k_1 = 1$ und $\tau_1 = 0$   ⇒   $r_1(t) = s(t)$ erhält man:

\[r(t) = s(t) + k_0 \cdot s( t - \tau_0) \hspace{0.05cm}.\]

Aus diesem vereinfachten Modell (ohne den grau hinterlegten Block in der Grafik) lassen sich wichtige Beschreibungsgrößen einfach berechnen:

• Wendet man den Verschiebungssatz an, so kommt man zur Übertragungsfunktion

\[H(f) = {R(f)}/{S(f)} = 1 + k_0 \cdot {\rm e}^{ - {\rm j} \cdot 2 \pi f \cdot \tau_0} \hspace{0.05cm}.\]

• Durch Fourierrücktransformation erhält man dann die Impulsantwort

\[h(\tau) = 1 + k_0 \cdot \delta(\tau - \tau_0) \hspace{0.05cm}.\]

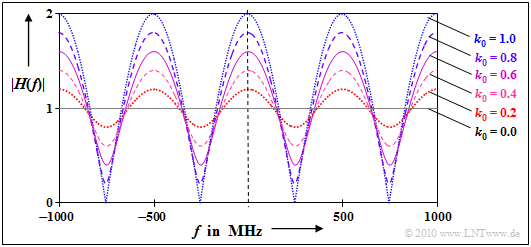
$\text{Beispiel 1:}$  Wir betrachten einen Zweiwegekanal mit Verzögerungszeit $\tau_0 = 2 \ \rm \mu s$ und verschiedene Dämpfungsfaktoren $k_0$ zwischen $0$ und $1$.

Betrag der Übertragungsfunktion eines Zweiwegekanals (τ₀ = 10 μs)

Die Grafik zeigt den Betrag der Übertragungsfunktion im Bereich zwischen $\pm 1000 \ \rm kHz$.

Man erkennt aus dieser Darstellung:

• Die Übertragungsfunktion $H(f)$ und auch deren Betrag ist periodisch mit $1/\tau_0 = 500 \ \rm kHz$.

• Diese Frequenzperiode ist hier gleichzeitig die sogenannte Kohärenzbandbreite .
  

• Die Schwankungen um den Mittelwert $\vert H(f) \vert = 1$ sind um so stärker, je größer der (relative) Beitrag $k_0$ des Nebenpfades (also das Echo) ist.

Kohärenzbandbreite in Abhängigkeit von M

Wir modifizieren nun das Zweiwegemodell dahingehend, dass wir mehr als zwei Pfade zulassen, wie es auch für den Mobilfunk zutrifft. Allgemein lautet somit das Mehrwege–Kanalmodell:

\[r(t) = \sum_{m = 1}^{M}\hspace{0.15cm} k_m \cdot s( t - \tau_m) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} h(\tau) = \sum_{m = 1}^{M}\hspace{0.15cm} k_m \cdot \delta( \tau - \tau_m) \hspace{0.05cm}.\]

Wir vergleichen nun den Zweiwegekanal $(M = 2)$ mit den Parametern

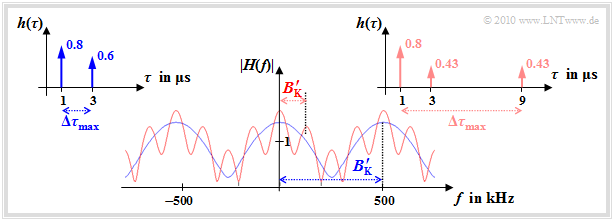
\[\tau_1 = 1\,\,{\rm \mu s}\hspace{0.05cm}, \hspace{0.2cm} k_1 = 0.8\hspace{0.05cm}, \hspace{0.2cm} \tau_2 = 3\,\,{\rm \mu s}\hspace{0.05cm}, \hspace{0.2cm} k_2 = 0.6\]

und den folgenden Dreiwegekanal $(M = 3)$:

\[\tau_1 = 1\,\,{\rm \mu s}\hspace{0.05cm}, \hspace{0.2cm} k_1 = 0.8\hspace{0.05cm}, \hspace{0.2cm} \tau_2 = 3\,\,{\rm \mu s}\hspace{0.05cm}, \hspace{0.2cm} k_2 \approx 0.43\hspace{0.05cm}, \hspace{0.2cm} \tau_3 = 9\,\,{\rm \mu s}\hspace{0.05cm}, \hspace{0.2cm} k_3 \approx 0.43 \hspace{0.05cm}.\]

Bei den gewählten Konstanten weisen beide Kanäle den quadratischen Mittelwert ${\rm E}[k_m^2] = 1$ auf.

Betragsfrequenzgang bei M = 2 (blau) und M = 3 (rot)

Die Grafik zeigt die Betragsfunktionen $ |H(f)|$ beider Kanäle und die zugehörigen Impulsantworten $h(\tau)$. Man erkennt aus diesen Darstellungen:

• Beim blauen Kanal $(M = 2)$ treten die Diracfunktionen in einem Bereich der Breite $\Delta \tau_{\rm max} = 2 \ \rm \mu s$ auf. Beim roten Kanal $(M = 3)$ ist dieser Wert viermal so groß:   $\Delta \tau_{\rm max} = 8 \ \rm \mu s$.
  

• Als erste Näherung für die noch zu definierende Kohärenzbandbreite $B_{\rm K}$ verwendet man oft $1/ \Delta \tau_{\rm max}$, die allerdings vom richtigen Wert um den Faktor $2$ und mehr abweichen kann.
  

• Die durch das Hochkomma bezeichnete einfache Näherung ergibt sich beim blauen Kanal zu $B_{\rm K}\hspace{0.01cm}'= 500 \ \rm kHz$, beim roten Kanal ist diese mit $B_{\rm K}\hspace{0.01cm}'= 125 \ \rm kHz$ um den Faktor $4$ kleiner.
  

• Allgemein gilt: Ist die Signalbandbreite $B_{\rm S} = 1/T_{\rm S}$ sehr viel kleiner als $B_{\rm K}$, so kann der Kanal für dieses System als nichtfrequenzselektiv betrachtet werden ($T_{\rm S}$ bezeichnet die Symboldauer).
  

• Anders ausgedrückt: Bei gegebenem $B_{\rm S}$ spielt die Frequenzselektivität eine um so größere Rolle, je kleiner die Kohärenzbandbreite $B_{\rm K}$ bzw. je größer die maximale Verzögerung $\Delta \tau_{\rm max}$ ist.
  

• Das bedeutet auch: Die Frequenzselektivität wird oft durch das längste Echo bestimmt. Viele kurze Echos mit der Gesamtenergie $E$ sind weniger störend als ein langes Echo gleicher Energie $E$.
  

Berücksichtigung der Zeitvarianz

Bisher wurden die Dämpfungsfaktoren $k_m$ als konstant angenommen. Für den Mobilfunk ist dieses Kanalmodell aber nur dann richtig, wenn sich Sender und Empfänger nicht bewegen, was für dieses Kommunikationssystem lediglich ein Sonderfall ist.

Für einen sich bewegenden Teilnehmer müssen diese konstanten Faktoren $k_m$ durch die zeitvarianten Größen $z_m(t)$ ersetzt werden, die jeweils auf Zufallsprozessen basieren. Es ist zu beachten:

• Die Beträge der komplexen Gewichtsfaktoren $z_m(t)$ sind rayleighverteilt entsprechend der Seite Signalverläufe bei Rayleigh–Fading oder – bei Sichtverbindung – riceverteilt, wie in Signalverläufe bei Rice–Fading beschrieben.
  

• Die Bindungen innerhalb des Zufallsprozesses $z_m(t)$ hängen über das Jakes–Spektrum mit den Mobilitätseigenschaften (Geschwindigkeit, Fahrtrichtung, usw.) zusammen.
  
  

Mobilfunkkanalmodell unter Berücksichtigung von Zeitvarianz und Echos

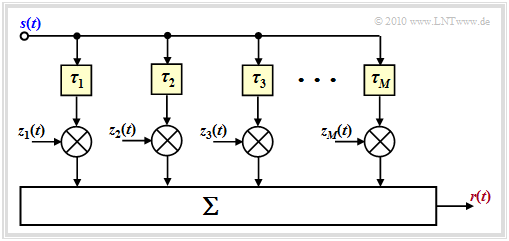
Nebenstehende Grafik zeigt das allgemeingültige Modell für den Mobilfunkkanal. „Allgemeingültig” allerdings nur unter Vorbehalt, wie am Seitenende noch ausgeführt wird. Zum Verständnis des Bildes verweisen wir auf das Kapitel Allgemeine Beschreibung des Mobilfunkkanals. Zu beachten ist:

• Die $M$ Hauptpfade des Modells sind durch große Laufzeitunterschiede gekennzeichnet.
• Die zeitvarianten komplexen Koeffizienten $z_m(t)$ ergeben sich aus der Summe vieler Nebenpfade ergeben, deren Verzögerungszeiten näherungsweise gleich $\tau_m$ sind.

$\text{Beispiel 2:}$  Untersuchungen haben ergeben, dass im Mobilfunk gleichzeitig nicht mehr als vier oder fünf Hauptpfade wirksam sind.

2D–Impulsantwort mit M = 3 Pfaden

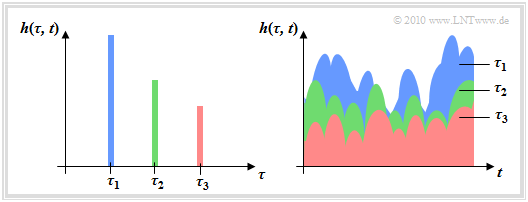
Die dargestelle 2D–Impulsantwort $h(\tau,\hspace{0.05cm} t)$ gilt für $M = 3$ Hauptpfade mit zeitvariantem Verhalten, bei denen die Empfangsleistung mit größer werdender Verzögerung im statistischen Mittel abnimmt. Für diese Grafik ist das oben skizzierrte Kanalmodell zugrundegelegt.

Dargestellt sind zwei verschiedene Ansichten:

• Das linke Bild zeigt $h(\tau,\hspace{0.05cm} t)$ in Abhängigkeit der Verzögerungszeit $\tau$ zu einem festen Zeitpunkt $t$.
• Im rechten Bild ist die Betrachtungsrichtung um $90^\circ$ gedreht. Aufgrund der farblichen Zuordnungen müsste die Darstellung verständlich sein.
  

Man erkennt aus diesem Bild auch die Schwachstelle des Modells: Zwar sind die Koeffizienten $z_m(t)$ variabel, aber die Verzögerungszeiten $\tau_m$ sind fest vorgegeben. Dies entspricht nicht der Realität, wenn die Funkverbindung aufgrund der sich bewegenden Mobilstation in einer sich ändernden Umgebung erfolgt.

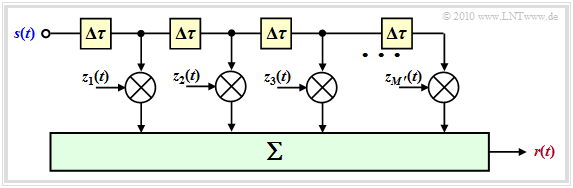
$\text{Fazit:}$  Man kann sich helfen, indem man das oben angegebene Modell wie folgt modifiziert:

Allgemeingültiges Modell des Mobilfunkkanals

• Man wählt die Anzahl $M'$ der (möglichen) Hauptpfade sehr viel größer, als es erforderlich wäre, und setzt $\tau_m = m \cdot \Delta \tau$.
• Die inkrementelle (minimal auflösbare) Verzögerung $\Delta \tau = T_{\rm S}$ ergibt sich aus der Abtastrate und damit der Bandbreite $B_{\rm S} = 1T_{\rm S}$ des Sendesignals.
  
• Die Maximalverzögerung $\tau_\text{max} = M' \cdot \Delta \tau$ dieses Kanalmodells ergibt sich aus dem Kehrwert der Kohärenzbandbreite $B_{\rm K}$.
• Damit liegt die Anzahl der berücksichtigten Pfade durch $M' = B_{\rm S}/B_{\rm K}$ eindeutig fest.

Auch hier liefern meist nicht mehr als $M = 5$ Hauptpfade gleichzeitig einen relevanten Beitrag zur Impulsantwort. Der Vorteil gegenüber dem ersten Modell ist, dass für die Verzögerungen nun alle Werte $\tau_m \le \tau_\text{max}$ mit einer zeitlichen Auflösung von $\Delta \tau$ möglich sind.

Am Ende des GWSSUS–Kapitels werden wir nochmals auf dieses allgemeine Modell zurückkommen.

Aufgaben zum Kapitel

Aufgabe 2.2: Einfaches Zweiwege–Modell