Difference between revisions of "Aufgaben:Exercise 1.11Z: Syndrome Decoding again"
(Die Seite wurde neu angelegt: „{{quiz-Header|Buchseite=Kanalcodierung/Decodierung linearer Blockcodes }} [[File:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice Frage…“) |
|||
| Line 4: | Line 4: | ||
}} | }} | ||
| − | [[File:|right|]] | + | [[File:P_ID2399__KC_Z_1_10.png|right|frame|Schaubild der Prüfgleichungen]] |
| + | Betrachtet wird die gleiche Konstellation wie in der [[Aufgaben:1.11_Syndromdecodierung|Aufgabe 1.11]], nämlich die Decodierung eines (7, 4, 3)–Hamming–Codes mit der Prüfmatrix | ||
| + | |||
| + | :$${ \boldsymbol{\rm H}}_{\rm } = \begin{pmatrix} 1 &1 &0 &1 &1 &0 &0\\ 0 &1 &1 &1 &0 &1 &0\\ 1 &0 &1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm}.$$ | ||
| + | |||
| + | Dementsprechend lautet das Generatorpolynom: | ||
| + | |||
| + | :$${ \boldsymbol{\rm G}} = \begin{pmatrix} 1 &0 &0 &0 &1 &0 &1\\ 0 &1 &0 &0 &1 &1 &0\\ 0 &0 &1 &0 &0 &1 &1\\ 0 &0 &0 &1 &1 &1 &1 \end{pmatrix}\hspace{0.05cm}.$$ | ||
| + | |||
| + | Bei der [[Kanalcodierung/Decodierung_linearer_Blockcodes#Prinzip_der_Syndromdecodierung|Syndromdecodierung]] bildet man aus dem Empfangsvektor <u>''y''</u> das Syndrom <u>''s''</u>: | ||
| + | |||
| + | :$$\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H}}^{\rm T} \in {\rm GF}(2^m) \hspace{0.05cm}.$$ | ||
| + | |||
| + | Mit diesem Ergebnis lässt sich beim betrachteten Hamming–Code ein jeder Einzelfehler im Codewort korrigieren. Im fehlerfreien Fall gilt $\underline{s} = \underline{s}_{0} = (0, 0, 0)$. Aber auch bei 3 Übertragungsfehlern kann sich unter Umständen $\underline{s}_{0} = (0, 0, 0)$ ergeben, so dass diese Fehler unerkannt bleiben. | ||
| + | |||
| + | ''Hinweis:'' | ||
| + | |||
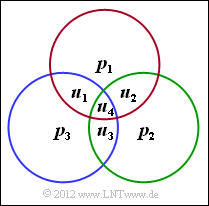
| + | Die Aufgabe bezieht sich auf die im Kapitel [[Kanalcodierung/Decodierung_linearer_Blockcodes|Decodierung linearer Blockcodes]] behandelte Thematik. Weitere Informationen zur Syndromdecodierung finden Sie im Angabenblatt zur [[Aufgaben:1.11_Syndromdecodierung|Aufgabe 1.11]]. Die Grafik verdeutlicht die drei Prüfgleichungen entsprechend der Prüfmatrix: | ||
| + | *erste Zeile: rote Gruppierung, | ||
| + | *zweite Zeile: grüne Gruppierung, | ||
| + | *dritte Zeile: blaue Gruppierung. | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | |
| + | |||
| + | {Handelt es sich um einen systematischen Code? | ||
| + | |type="[]"} | ||
| + | + Ja, | ||
| + | - Nein. | ||
| + | |||
| + | {Empfangen wurde $\underline{y} = (1, 0, 0, 1, 0, 1, 0)$. Ist dies ein gültiges Codewort? | ||
|type="[]"} | |type="[]"} | ||
| − | - | + | + Ja, |
| − | + | - Nein. | |
| + | {Welches Syndrom ergibt sich mit diesem Empfangswort? | ||
| + | |type="[]"} | ||
| + | + $\underline{s} = \underline{s}_{0} = (0, 0, 0),$ | ||
| + | - $\underline{s} = \underline{s}_{3} = (0, 1, 1),$ | ||
| + | - $\underline{s} = \underline{s}_{7} = (1, 1, 1).$ | ||
| + | |||
| + | {Welche Empfangsworte führen zum gleichen Syndrom wie in Teilaufgabe (3)? | ||
| + | |type="[]"} | ||
| + | - $\underline{y} = (1, 1, 0, 1, 0, 1, 0),$ | ||
| + | + $\underline{y} = (0, 1, 0, 1, 0, 0, 1),$ | ||
| + | + $\underline{y} = (0, 1, 1, 0, 1, 0, 1).$ | ||
| − | |||
| − | |||
| − | |||
| Line 26: | Line 61: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' |
'''2.''' | '''2.''' | ||
'''3.''' | '''3.''' | ||
Revision as of 17:37, 8 December 2017
Betrachtet wird die gleiche Konstellation wie in der Aufgabe 1.11, nämlich die Decodierung eines (7, 4, 3)–Hamming–Codes mit der Prüfmatrix
- $${ \boldsymbol{\rm H}}_{\rm } = \begin{pmatrix} 1 &1 &0 &1 &1 &0 &0\\ 0 &1 &1 &1 &0 &1 &0\\ 1 &0 &1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm}.$$
Dementsprechend lautet das Generatorpolynom:
- $${ \boldsymbol{\rm G}} = \begin{pmatrix} 1 &0 &0 &0 &1 &0 &1\\ 0 &1 &0 &0 &1 &1 &0\\ 0 &0 &1 &0 &0 &1 &1\\ 0 &0 &0 &1 &1 &1 &1 \end{pmatrix}\hspace{0.05cm}.$$
Bei der Syndromdecodierung bildet man aus dem Empfangsvektor y das Syndrom s:
- $$\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H}}^{\rm T} \in {\rm GF}(2^m) \hspace{0.05cm}.$$
Mit diesem Ergebnis lässt sich beim betrachteten Hamming–Code ein jeder Einzelfehler im Codewort korrigieren. Im fehlerfreien Fall gilt $\underline{s} = \underline{s}_{0} = (0, 0, 0)$. Aber auch bei 3 Übertragungsfehlern kann sich unter Umständen $\underline{s}_{0} = (0, 0, 0)$ ergeben, so dass diese Fehler unerkannt bleiben.
Hinweis:
Die Aufgabe bezieht sich auf die im Kapitel Decodierung linearer Blockcodes behandelte Thematik. Weitere Informationen zur Syndromdecodierung finden Sie im Angabenblatt zur Aufgabe 1.11. Die Grafik verdeutlicht die drei Prüfgleichungen entsprechend der Prüfmatrix:
- erste Zeile: rote Gruppierung,
- zweite Zeile: grüne Gruppierung,
- dritte Zeile: blaue Gruppierung.
Fragebogen
Musterlösung