Aufgaben:Exercise 4.5Z: Tangent Hyperbolic and Inverse

• Return to book

Tabelle $y = \tanh {(x)}$

Im Theorieteil wurde am Beispiel des Single Parity–check Codes gezeigt, dass der extrinsische $L$–Wert bezüglich des $i$–ten Symbols wie folgt definiert ist:

$$L_{\rm E}(i) = {\rm ln} \hspace{0.2cm}\frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} \hspace{0.05cm}.$$

Diese Gleichung ist auch bei vielen anderen Kanalcodes anwendbar. Das Codewort $\underline{x}^{(-i)}$ in dieser Definition beinhaltet alle Symbole mit Ausnahme von $x_i$ und hat somit die Länge $n-1$.

In der Aufgabe A4.4 wurde gezeigt, dass der extrinsische $L$–Wert auch wie folgt geschrieben werden kann:

$$L_{\rm E}(i) = {\rm ln} \hspace{0.2cm} \frac{1 + \pi}{1 - \pi}\hspace{0.05cm}, \hspace{0.3cm} {\rm mit} \hspace{0.3cm} \pi = \prod\limits_{j \ne i}^{n} \hspace{0.15cm}{\rm tanh}(L_j/2) \hspace{0.05cm}.$$

In dieser Aufgabe soll nun nach einer weiteren Berechnungsmöglichkeit gesucht werden.

Hinweise:

• Die Aufgabe gehört zum Themengebiet von Kapitel 4.1.
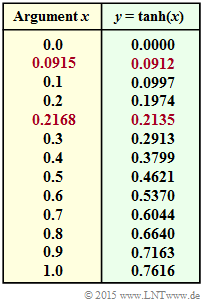
• Rechts oben sehen Sie eine Tabelle mit den Zahlenwerten der Funktion $y = \tanh {(x)}$  ⇒  Tangens Hyperbolikus. Mit den rot hinterlegten Zeilen kann man die Werte der inversen Funktion $x = \tanh^{-1}{(y)}$ ablesen, die für die Teilaufgabe (5) benötigt werden.

Fragebogen

1

Es gelte $\underline{L}_{\rm APP} = (+1.0, +0.4, -1.0)$. Berechnen Sie die extrinsischen $L$–Werte  ⇒  $\underline{L}_E = (L_{\rm E}(1), \ L_{\rm E}(2), \ L_{\rm E}(3))$ nach der vorne angegebenen Gleichung:

$L_{\rm E}(1) \ = \ $

$L_{\rm E}(2) \ = \ $

$L_{\rm E}(3) \ = \ $

2

Welche der Eigenschaften weist die Funktion $y = \tanh {(x)}$ auf?

	Es gilt $\tanh {(x)} = (e^x - e^{-x}) \ / \ (e^x + e^{-x})$.
	Es gilt $\tanh {(x)} = (1 - e^{-2x}) \ / \ (1 + e^{-2x})$.
	Die Funktion $y = \tanh {(x)}$ ist für alle $x$–Werte definiert.
	Es gilt $y_{\rm min} = 0$ und $y_{\rm max} → ∞$
	Es gilt $y_{\rm min} = -1$ und $y_{\rm max} = +1$.

3

Welche Eigenschaften weist die inverse Funktion $x = \tanh^{(-1)}{(y)}$ auf?

	Die Funktion $x = \tanh^{-1}{(y)}$ ist für alle $y$–Werte definiert.
	Es gilt $x = \tanh^{-1}{(y)} = 1/2 \cdot \ln {[(1 + y) \ / \ (1 - y)]}$.
	Es gilt $x_{\rm min} = -1$ und $x_{\rm max} = +1$.
	Es gilt $x_{\rm min} → -∞$ und $x_{\rm max} → +∞$.

4

Wie lässt sich $L_{\rm E}(i)$ auch darstellen? Es sei $\pi$ wie auf der Angabenseite definiert.

	Es gilt $L_{\rm E}(i) = \tanh^{-1}{(\pi)}$.
	Es gilt $L_{\rm E}(i) = 2 \cdot \tanh^{-1}{(\pi)}$.
	Es gilt $L_{\rm E}(i) = 2 \cdot \tanh^{-1}{\ln {[(1 + \pi) \ / \ (1 - \pi)]}}$.

5

Berechnen Sie die extrinsischen $L$–Werte mit der Gleichung gemäß Aufgabe (4). Verwenden Sie hierzu die Tabelle auf der Angabenseite.

$L_{\rm E}(1) \ = \ $

$L_{\rm E}(2) \ = \ $

$L_{\rm E}(3) \ = \ $

Musterlösung

Solution

(1)  Entsprechend der Angabe gilt:

$$L_{\rm E}(i) = {\rm ln} \hspace{0.2cm} \frac{1 + \pi}{1 - \pi}\hspace{0.05cm}, \hspace{0.3cm} {\rm mit} \hspace{0.3cm} \pi = \prod\limits_{j \ne i}^{3} \hspace{0.15cm}{\rm tanh}(L_j/2) \hspace{0.05cm}.$$

Aus der Tabelle auf der Angabenseite kann abgelesen werden:

$$\tanh {(L_1/2)} = \tanh {(0.5)} = 0.4621$,$$

$$\tanh {(L_2/2)} = \tanh {(0.2)} = 0.1974.$$

Da der Tangens Hyperbolikus eine ungerade Funktion ist, gilt weiter

$$\tanh {(L_3/2)} = -\tanh {(0.5)} = -0.4621.$$

• Berechnung von $L_{\rm E}(1)$:

$$\pi = {\rm tanh}(L_2/2) \cdot {\rm tanh}(L_3/2) = (+0.1974) \cdot (-0.4621) = - 0.0912$$

$$\Rightarrow \hspace{0.3cm} L_{\rm E}(1) = {\rm ln} \hspace{0.2cm} \frac{1 -0.0912}{1 +0.0912}\hspace{0.15cm}\underline{=-0.1829} \hspace{0.05cm}.$$

• Berechnung von $L_{\rm E}(2)$:

$$\pi = {\rm tanh}(L_1/2) \cdot {\rm tanh}(L_3/2) = (+0.4621) \cdot (-0.4621) = - 0.2135$$

$$\Rightarrow \hspace{0.3cm} L_{\rm E}(2) = {\rm ln} \hspace{0.2cm} \frac{1 -0.2135}{1 +0.2135}\hspace{0.15cm}\underline{=-0.4337} \hspace{0.05cm}.$$

• Berechnung von $L_{\rm E}(3)$:

$$\pi = {\rm tanh}(L_1/2) \cdot {\rm tanh}(L_2/2) = (+0.4621) \cdot (+0.1974) = + 0.0912$$

$$\Rightarrow \hspace{0.3cm} L_{\rm E}(3) = {\rm ln} \hspace{0.2cm} \frac{1 +0.0912}{1 -0.0912}\hspace{0.15cm}\underline{=+0.1829}= - L_{\rm E}(1) \hspace{0.05cm}.$$

(2)  Richtig sind die Lösungsvorschläge 1, 2, 3 und 5: Die Funktion

$$y ={\rm tanh}(x) = \frac{{\rm e}^{x}-{\rm e}^{-x}}{{\rm e}^{x}+{\rm e}^{-x}} = \frac{1-{\rm e}^{-2x}}{1+{\rm e}^{-2x}}$$

ist für alle $x$–Werte berechenbar und es gilt $\tanh{(-x)} = -\tanh{(x)}$. Für große Werte von $x$ wird $e^{-x}$ sehr klein, so dass man im Grenzfall $x → ∞$ den Grenzwert $y = 1$ erhält.

(3)  Da der Tangens Hyperbolikus nur Werte zwischen $±1$ liefert, ist die Umkehrfunktion $x = \tanh^{-1}{(y)}$ auch nur für $|y| ≤ 1$ auswertbar. Durch Umstellen der angegebenen Gleichung

$$x ={\rm tanh}^{-1}(y) = 1/2 \cdot {\rm ln} \hspace{0.2cm} \frac{1+y}{1-y}$$

erhält man:

$${\rm e}^{2x} = \frac{1+y}{1-y} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\rm e}^{-2x} = \frac{1-y}{1+y} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} (1+y) \cdot {\rm e}^{-2x} = 1-y $$

$$\Rightarrow \hspace{0.3cm}y = \frac{1-{\rm e}^{-2x}}{1+{\rm e}^{-2x}} = {\rm tanh}(x) \hspace{0.05cm}.$$

Das bedeutet:

• Die im Lösungsvorschlag 2 angegebene Gleichung ist richtig.
• Im Grenzfall $y → 1$ gilt $x = tanh^{-1}{(y)} →$.
• Auch die Umkehrfunktion ist ungerade  ⅸ  im Grenzfall $y → -1$ geht $x → -∞$.

Richtig sind demnach die Lösungsvorschläge 2 und 4.

(4)  Ausgehend von der Gleichung

$$L_{\rm E}(i) = {\rm ln} \hspace{0.2cm} \frac{1 + \pi}{1 - \pi}$$

kommt man mit dem Ergebnis von (3) zur äquivalenten Gleichung entsprechend dem Lösungsvorschlag 2:

$$L_{\rm E}(i) = 2 \cdot {\rm tanh}^{-1}(\pi)\hspace{0.05cm}.$$

(5)  Mit dem Ergebnis der Teilaufgabe (1) erhält man

• für den ersten extrinsischen $L$–Wert, da $\pi_1 = -0.0912$:

$$L_{\rm E}(1) = 2 \cdot {\rm tanh}^{-1}(-0.0912)= -2 \cdot {\rm tanh}^{-1}(0.0912) = -2 \cdot 0.0915\hspace{0.15cm}\underline{=-0.1830} \hspace{0.05cm}.$$

• für den zweiten extrinsischen $L$–Wert, da $\pi_2 = -0.2135$:

$$L_{\rm E}(2) = -2 \cdot {\rm tanh}^{-1}(0.2135) = -2 \cdot 0.2168\hspace{0.15cm}\underline{=-0.4336} \hspace{0.05cm}.$$

• für den dritten extrinsischen $L$–Wert, da $\pi_3 = +0.0912 = -\pi_1$:

$$L_{\rm E}(3) = -L_{\rm E}(1) \hspace{0.15cm}\underline{=+0.1830} \hspace{0.05cm}.$$

Das Ergebnis wurde mit Hilfe der roten Tabelleneinträge auf der Angabenseite ermittelt und stimmt bis auf Rundungsfehler (Multiplikation/Division durch $2$) mit den Ergebnissen der Teilaufgabe (1) überein.