Difference between revisions of "Aufgaben:Exercise 4.7: Product Code Decoding"
| Line 66: | Line 66: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' | '''(1)''' | ||
| + | |||
| + | |||
'''(2)''' | '''(2)''' | ||
| + | |||
| + | |||
'''(3)''' | '''(3)''' | ||
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 12:58, 10 December 2017
Wir betrachten wie in Aufgabe A4.6 einen Produktcode, basierend auf
- dem Hammingcode (7, 4, 3) ⇒ Code $C_1$,
- dem verkürzten Hammingcode (6, 3, 3) ⇒ $C_2$.
Die Prüfmatrizen dieser Codes lauten:
- $${ \boldsymbol{\rm H}}_1 = \begin{pmatrix} 1 &1 &0 &1 &1 &0 &0 \\ 0 &1 &1 &1 &0 &1 &0 \\ 1 &0 &1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm},$$
- $${ \boldsymbol{\rm H}}_2 = \begin{pmatrix} 1 &1 &0 &1 &0 &0 \\ 1 &0 &1 &0 &1 &0 \\ 0 &1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm}.$$
Die Hard Decision Decodierung dieses Codes geschieht vorzugsweise iterativ, indem abwechselnd alle Zeilen und anschließend alle Spalten syndromdecodiert werden.
Hinweis: Die Syndromdecodierung soll entsprechend der zweiten Theorieseite von Kapitel 4.2 erfolgen.
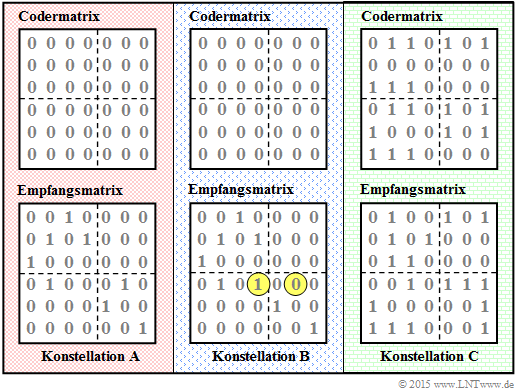
Die folgende Grafik zeigt drei verschiedene Coder– und Empfangsmatrizen, die in den Teilaufgaben (1), (2) und (3) zu analysieren sind. Wir benennen diese mit Konstellation (A), (B) und (C). Gelb markiert sind die Unterschiede der Empfangsmatrix von Konstellation (B) gegenüber (A). In beiden Fällen besteht die Codermatrix nur aus Nullen. Die Codematrix von (C) wurde in Aufgabe A4.6 ermittelt.
Die Syndromdecodierung (eindimensionaler) Blockcodes wurde bereits im Kapitel Decodierung linearer Blockcodes behandelt. Hier eine kurze Zusammenfassung und eine Adaption an den zweidimensionalen Fall:
- Aus dem Empfangswort $\underline{y}$ (einer Zeile bzw. einer Spalte der vorgegebenen Empfangsmatrix) wird das Syndrom entsprechend $\underline{s} = \underline{y} \cdot \mathbf{H}_1^{\rm T}$ bzw. $\underline{s} = \underline{y} \cdot \mathbf{H}_2^{\rm T}$ gebildet.
- Mit dem Ergebnis $\underline{s} = \underline{s}_{\mu}$ kann man in obigen Tabellen den so genannten Nebenklassenanfüherer $\underline{e}_{\mu}$ ablesen. Das korrigierte Codewort ist dann $\underline{y} + \underline{e}_{\mu}$.
Fragebogen
Musterlösung
(2)
(3)