Aufgaben:Exercise 4.12: Regular and Irregular Tanner Graph

• Return to book

Vorgegebener Tanner–Graph für Code A

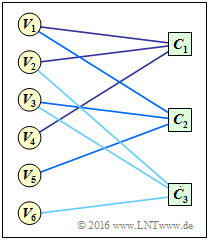
Dargestellt ist ein Tanner–Graph eines Codes A mit

• den Variable Nodes (abgekürzt VNs) $V_1, \ ... \ , \ V_6$, wobei $V_i$ das $i$–te Codewortbit kennzeichnet (egal, ob Informations – oder Paritybit) und der $i$–ten Spalte der Prüfmatrix entspricht;
• den Check Nodes (abgekürzt CNs) $C_1, \ ... \ , \ C_3$, die die Zeilen der $\mathbf{H}_{\rm A}$–Matrix und damit die Prüfgleichungen repräsentieren.

Eine Verbindungslinie (englisch: Edge) zwischen $V_i$ und $C_j$ zeigt an, dass das $i$–te Codewortsymbol an der $j$–ten Prüfgleichung beteiligt ist. In diesem Fall ist das Element $h_{j,i}$ der Prüfmatrix gleich $1$.

In der Aufgabe soll der Zusammenhang zwischen dem oben dargestellten Tanner–Graphen (gültig für den Code A) und der Matrix $\mathbf{H}_{\rm A}$ angegeben werden. Außerdem ist der Tanner–Graph zu einer Prüfmatrix $\mathbf{H}_{\rm B}$ aufzustellen, die sich aus $\mathbf{H}_{\rm A}$ durch Hinzufügen einer weiteren Zeile ergibt. Diese ist so zu ermitteln, dass der zugehörige Code B regulär ist. Das bedeutet:

• Von allen Variable Nodes $V_i$ (mit $1 ≤ i ≤ n$) gehen gleich viele Linien (Edges) ab, ebenso von allen Check Nodes $C_j$ (mit $1 ≤ j ≤ m$).
• Die Hamming–Gewichte aller Zeilen von $\mathbf{H}_{\rm B}$ sollen jeweils gleich sein $(w_{\rm Z})$, ebenso die Hamming–Gewichte aller Spalten $(w_{\rm S})$.
• Für die Rate des zu konstruierenden regulären Codes B gilt dann die folgende untere Schranke:

$$R \ge 1 - \frac{w_{\rm S}}{w_{\rm Z}} \hspace{0.05cm}.$$

Hinweis:

• Die Aufgabe gehört zum Themengebiet des Kapitels Grundlegendes zu den Low–density Parity–check Codes.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Wieviele Zeilen $(m)$ und Spalten $(n)$ hat die Prüfmatrix $\mathbf{H}_{\rm A}$?

$m \ = \ $

$n \ = \ $

2

Welche Aussagen sind aufgrund des Tanner–Graphen zutreffend?

	Die erste Zeile der $\mathbf{H}_{\rm A}$–Matrix ist „$1 \ 1 \ 0 \ 1 \ 0 \ 0$”..
	Die zweite Zeile der $\mathbf{H}_{\rm A}$–Matrix ist „$1 \ 0 \ 1 \ 0 \ 0 \ 1$”.
	Die dritte Zeile der $\mathbf{H}_{\rm A}$–Matrix ist „$0 \ 1 \ 1 \ 0 \ 0 \ 1$”.

3

Welche Eigenschaften weist der Code A auf?

	Der Code ist systematisch.
	Der Code ist regulär.
	Die Coderate ist $R = 1/2$.
	Die Coderate ist $R = 1/3$.

4

Die Matrix $\mathbf{H}_{\rm B}$ ergibt sich aus $\mathbf{H}_{\rm A}$ durch Hinzufügen einer weiteren Zeile. Durch welche Zeile 4 ergibt sich ein regulärer Code B?

	Durch Hinzufügen von „$0 \ 0 \ 0 \ 1 \ 1 \ 1$”.
	Durch Hinzufügen von „$1 \ 1 \ 1 \ 1 \ 1 \ 1$”.
	Durch Hinzufügen irgend einer anderen Zeile.

5

Welche Eigenschaften weist der Code B auf?

	Der Code ist systematisch.
	Der Code ist regulär.
	Die Coderate ist $R = 1/2$.
	Die Coderate ist $R = 1/3$.

Musterlösung

Solution

(1)  (2)  (3)  (4)  (5)