Difference between revisions of "Aufgaben:Exercise 4.5: Pseudo Noise Modulation"

Revision as of 17:57, 14 December 2017

Ersatzschaltbild von PN-Modulation und BPSK

Die Grafik zeigt das Ersatzschaltbild der PN–Modulation (engl. Direct Sequence Spread Spectrum, abgekürzt DS–SS) im äquivalenten TP–Bereich. $n(t)$ ist AWGN–Rauschen. Unten ist das TP–Modell der binären Phasenmodulation (BPSK) skizziert. Das Tiefpass–Sendesignal $s(t)$ ist nur aus Gründen einheitlicher Darstellung gleich dem rechteckförmigen Quellensignal $q(t) ∈ \{+1, –1\}$ mit Rechteckdauer $T$ gesetzt ist. Die Funktion des Integrators kann wie folgt geschrieben werden:

$$d (\nu T) = \frac{1}{T} \cdot \hspace{-0.3cm} \int_{(\nu -1 )T }^{\nu T} \hspace{-0.3cm} b (t )\hspace{0.1cm} {\rm d}t \hspace{0.05cm}.$$

Die beiden Modelle unterscheiden sich durch die Multiplikation mit dem $±1$–Spreizsignal $c(t)$ bei Sender und Empfänger, wobei von $c(t)$ lediglich der Spreizgrad $J$ bekannt ist. Für die Lösung dieser Aufgabe ist die Angabe der spezifischen Spreizfolge (M–Sequenz oder Walsh–Funktion) nicht von Bedeutung. Zu untersuchen ist, ob sich das untere BPSK–Modell auch bei PN–Modulation anwenden lässt und ob die BPSK–Fehlerwahrscheinlichkeit

$$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { \frac{2 \cdot E_{\rm B}}{N_{\rm 0}} } \hspace{0.05cm} \right )$$

auch für die PN–Modulation gültig ist, bzw. wie die angegebene Gleichung zu modifizieren ist.

Hinweis:

Die Aufgabe gehört zum Nachrichtentechnische Aspekte von UMTS . Das bei UMTS eingesetzte CDMA–Verfahren firmiert auch unter der Bezeichnung „PN–Modulation”. Die in dieser Aufgabe verwendete Nomenklatur richtet sich zum Teil PN–Modulation im Buch „Modulationsverfahren”.

Fragebogen

Musterlösung

Solution

(1) (2) (3) (4) (5) (6) (7)

@@ Line 1: / Line 1: @@
-{{quiz-Header|Buchseite=Beispiele von Nachrichtensystemen/Nachrichtentechnische Aspekte von UMTS
+{{quiz-Header|Buchseite=Beispiele von Nachrichtensystemen/Nachrichtentechnische Aspekte von UMTS}}
+[[File:P_ID1973__Mod_Z_5_2.png|right|frame|Ersatzschaltbild von PN-Modulation und BPSK]]
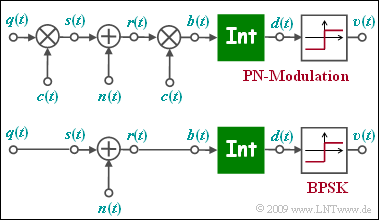
+Die Grafik zeigt das Ersatzschaltbild der PN–Modulation (engl. ''Direct Sequence Spread Spectrum'', abgekürzt DS–SS) im äquivalenten TP–Bereich. $n(t)$ ist AWGN–Rauschen.
+Unten ist das TP–Modell der binären Phasenmodulation (BPSK) skizziert.
+Das Tiefpass–Sendesignal $s(t)$ ist nur aus Gründen einheitlicher Darstellung gleich dem rechteckförmigen Quellensignal $q(t) ∈ \{+1, –1\}$ mit Rechteckdauer $T$ gesetzt ist. Die Funktion des Integrators kann wie folgt geschrieben werden:
+:$$d (\nu T) = \frac{1}{T} \cdot \hspace{-0.3cm} \int_{(\nu -1 )T }^{\nu T} \hspace{-0.3cm} b (t )\hspace{0.1cm} {\rm d}t \hspace{0.05cm}.$$
+Die beiden Modelle unterscheiden sich durch die Multiplikation mit dem $±1$–Spreizsignal $c(t)$ bei Sender und Empfänger, wobei von $c(t)$ lediglich der Spreizgrad $J$ bekannt ist. Für die Lösung dieser Aufgabe ist die Angabe der spezifischen Spreizfolge (M–Sequenz oder Walsh–Funktion) nicht von Bedeutung.
+Zu untersuchen ist, ob sich das untere BPSK–Modell auch bei PN–Modulation anwenden lässt und ob die BPSK–Fehlerwahrscheinlichkeit
+:$$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { \frac{2 \cdot E_{\rm B}}{N_{\rm 0}} } \hspace{0.05cm} \right )$$
+auch für die PN–Modulation gültig ist, bzw. wie die angegebene Gleichung zu modifizieren ist.
-}}
-[[File:|right|frame|]]
+''Hinweis:''
+Die Aufgabe gehört zum [[Beispiele_von_Nachrichtensystemen/Nachrichtentechnische_Aspekte_von_UMTS|Nachrichtentechnische Aspekte von UMTS
+]]. Das bei UMTS eingesetzte CDMA–Verfahren firmiert auch unter der Bezeichnung „PN–Modulation”. Die in dieser Aufgabe verwendete Nomenklatur richtet sich zum Teil [[Modulationsverfahren/PN–Modulation|PN–Modulation]] im Buch „Modulationsverfahren”.
 ===Fragebogen===

	Falsch
	Richtig