Difference between revisions of "Aufgaben:Exercise 2.2: Properties of Galois Fields"
| Line 2: | Line 2: | ||
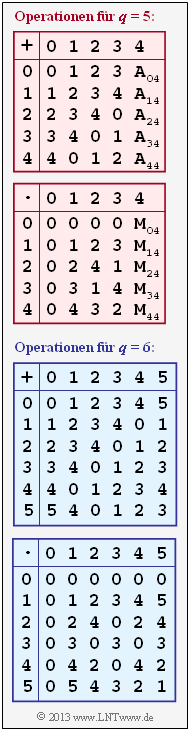
[[File:P_ID2492__KC_A_2_2.png|right|frame|Additions– und Multiplikationstabellen für $q = 5$ und $q = 6$]] | [[File:P_ID2492__KC_A_2_2.png|right|frame|Additions– und Multiplikationstabellen für $q = 5$ und $q = 6$]] | ||
| + | Wir betrachten hier die Zahlenmengen | ||
| + | * $Z_5 = \{0, \, 1, \, 2, \, 3, \, 4\} \ \Rightarrow \ q = 5$, | ||
| + | * $Z_6 = \{0, \, 1, \, 2, \, 3, \, 4,\, 5\} \ \Rightarrow \ q = 6$. | ||
| + | |||
| + | |||
| + | In nebenstehender Grafik sind die (teilweise unvollständigen) Additions– und Multiplikationstabellen für $q = 5$ und für $q = 6$ angegeben, wobei sowohl die Addition („$+$”) als auch die Multiplikation („$\cdot$”) modulo $q$ zu verstehen sind. | ||
| + | |||
| + | Zu überprüfen ist, ob die Zahlenmengen $Z_5$ und $Z_6$ alle Bedingungen eines Galoisfeldes $\rm GF(5)$ bzw. $\rm GF(6)$ erfüllen. Im [[Theorieteil]] werden insgesamt acht Bedingungen genannt, die alle erfüllt sein müssen. Von ihnen überprüft werden sollen nur zwei dieser Bedingungen: | ||
| + | |||
| + | (D) Für alle Elemente gibt es eine <span style="color: rgb(204, 0, 0);"><b>additive Inverse</b></span> (<i>Inverse for „$+$”</i> | ||
| + | :$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_A}(z_i) \in {\rm GF}(q):$$ | ||
| + | :$$\hspace{0.25cm}z_i + {\rm Inv_A}(z_i) = 0 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} | ||
| + | {\rm Inv_A}(z_i) = -z_i \hspace{0.05cm}.$$ | ||
| + | |||
| + | (E) Alle Elemente haben eine <span style="color: rgb(204, 0, 0);"><b>multiplikative Inverse</b></span> (<i>Inverse for „$\cdot$”</i>): | ||
| + | :$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} z_i \ne 0, \hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_M}(z_i) \in {\rm GF}(q):$$ | ||
| + | :$$\hspace{0.25cm}z_i \cdot {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} | ||
| + | {\rm Inv_M}(z_i) = z_i^{-1}\hspace{0.05cm}.$$ | ||
| + | |||
| + | Die weiteren Bedingungen für ein Galoisfeld, nämlich | ||
| + | * Closure, | ||
| + | * Existenz von Null– und Einselelement, | ||
| + | * Gültigkeit von Kommutativ– Assoziativ– und Distributivgesetz | ||
| + | |||
| + | |||
| + | werden sowohl von $Z_5$ als auch von $Z_6$ erfüllt. | ||
| + | |||
| + | ''Hinweis:'' | ||
| + | * Die Aufgabe bezieht sich auf das Kapitel [[...]]. | ||
| + | |||
Revision as of 23:44, 14 December 2017
Wir betrachten hier die Zahlenmengen
- $Z_5 = \{0, \, 1, \, 2, \, 3, \, 4\} \ \Rightarrow \ q = 5$,
- $Z_6 = \{0, \, 1, \, 2, \, 3, \, 4,\, 5\} \ \Rightarrow \ q = 6$.
In nebenstehender Grafik sind die (teilweise unvollständigen) Additions– und Multiplikationstabellen für $q = 5$ und für $q = 6$ angegeben, wobei sowohl die Addition („$+$”) als auch die Multiplikation („$\cdot$”) modulo $q$ zu verstehen sind.
Zu überprüfen ist, ob die Zahlenmengen $Z_5$ und $Z_6$ alle Bedingungen eines Galoisfeldes $\rm GF(5)$ bzw. $\rm GF(6)$ erfüllen. Im Theorieteil werden insgesamt acht Bedingungen genannt, die alle erfüllt sein müssen. Von ihnen überprüft werden sollen nur zwei dieser Bedingungen:
(D) Für alle Elemente gibt es eine additive Inverse (Inverse for „$+$”
- $$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_A}(z_i) \in {\rm GF}(q):$$
- $$\hspace{0.25cm}z_i + {\rm Inv_A}(z_i) = 0 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_A}(z_i) = -z_i \hspace{0.05cm}.$$
(E) Alle Elemente haben eine multiplikative Inverse (Inverse for „$\cdot$”):
- $$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} z_i \ne 0, \hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_M}(z_i) \in {\rm GF}(q):$$
- $$\hspace{0.25cm}z_i \cdot {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = z_i^{-1}\hspace{0.05cm}.$$
Die weiteren Bedingungen für ein Galoisfeld, nämlich
- Closure,
- Existenz von Null– und Einselelement,
- Gültigkeit von Kommutativ– Assoziativ– und Distributivgesetz
werden sowohl von $Z_5$ als auch von $Z_6$ erfüllt.
Hinweis:
- Die Aufgabe bezieht sich auf das Kapitel ....
Fragebogen
Musterlösung