Difference between revisions of "Aufgaben:Exercise 2.10: Reed-Solomon Error Detection"
From LNTwww
| Line 46: | Line 46: | ||
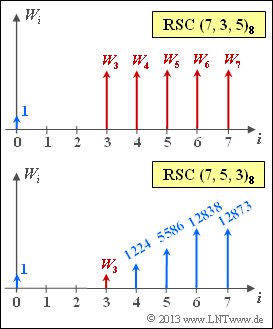
${\rm RSC} \, (7, \, 3, \, 5) \text{:} \hspace{0.2cm} W_3 \ = \ ${ 0 3% } | ${\rm RSC} \, (7, \, 3, \, 5) \text{:} \hspace{0.2cm} W_3 \ = \ ${ 0 3% } | ||
$\hspace{2.85cm} W_4 \ = \ ${ 0 3% } | $\hspace{2.85cm} W_4 \ = \ ${ 0 3% } | ||
| − | $\hspace{2. | + | $\hspace{2.85cm} W_5 \ = \ ${ 147 3% } |
| − | $\hspace{2. | + | $\hspace{2.85cm} W_6 \ = \ ${ 147 3% } |
| − | $\hspace{2. | + | $\hspace{2.85cm} W_7 \ = \ ${ 217 3% } |
{Wie lautet das in der Grafik fehlende Gewicht des $\rm RSC \, (7, \, 5, \, 3)_8$? | {Wie lautet das in der Grafik fehlende Gewicht des $\rm RSC \, (7, \, 5, \, 3)_8$? | ||
Revision as of 18:12, 16 December 2017
Bei einem linearen Blockcode können bis zu $e = d_{\rm min} - 1$ Fehler erkannt werden. Bei allen Reed–Solomon–Codes beträgt dabei die minimale Distanz
- $$d_{\rm min} = n-k+1 \hspace{0.05cm}.$$
Man muss folgende Fälle unterscheiden:
- Treten nicht mehr als $e = n - k$ Symbolfehler auf, so wird der Block als fehlerhaft erkannt.
- Die Fehlererkennung kann auch bei mehr als $n - k$ Symbolfehlern noch funktionieren, und zwar dann, wenn das Empfangswort kein gültiges Codewort des Reed–Solomon–Codes ist:
- $$\underline {y} \notin C_{\rm RS} = \{ \underline {c}_{\hspace{0.05cm}0}, \hspace{0.05cm}... \hspace{0.05cm}, \underline {c}_i, \hspace{0.05cm}... \hspace{0.05cm}, \underline {c}_{\hspace{0.05cm}n -1} \} \hspace{0.05cm}. $$
- Ist aber das verfälschte Empfangswort $(\underline{y} ≠ \underline{c})$ ein gültiges Codewort ⇒ $\underline{y}$, so bleibt bei der Decodierung der fehlerhafte Block unentdeckt. Wir definieren als Blockfehlerwahrscheinlichkeit.
- $${\rm Pr}({\rm Blockfehler}) = {\rm Pr}(\underline {y} \ne \underline {c}) \hspace{0.05cm}.$$
In dieser Aufgabe soll diese Wahrscheinlichkeit für folgende Codes ermittelt werden:
- Reed–Solomon–Code $(7, \, 3, \, 5)_8 \ \Rightarrow \ d_{\rm min} = 5$,
- Reed–Solomon–Code $(7, \, 5, \, 3)_8 \ \Rightarrow \ d_{\rm min} = 3$.
Weiterhin soll gelten:
- Jedes Symbol wird mit der Wahrscheinlichkeit $\epsilon_{\rm S} = 0.1$ in ein anderes Symbol verfälscht und mit der Wahrscheinlichkeit $1 - \epsilon_{\rm S} = 0.9$ richtig übertragen.
- Für das Distanzspektrum eines Reed–Solomon–Codes der Länge $n$ gilt mit $d = d_{\rm min}$:
- $$W_i = {n \choose i} \cdot \sum_{j = 0}^{i-d}\hspace{0.15cm}(-1)^j \cdot {i \choose j} \cdot \big [\hspace{0.03cm}q^{i\hspace{0.03cm}-\hspace{0.03cm}j\hspace{0.03cm}-\hspace{0.03cm}d\hspace{0.03cm}+\hspace{0.03cm}1}-1 \hspace{0.03cm} \big ]\hspace{0.05cm}.$$
Daneben sollen zwei Schranken für die Blockfehlerwahrscheinlichkeit betrachtet und bewertet werden:
- Ist allein die minimale Distanz bekannt, so kann man daraus eine obere Schranke ableiten. Die Gewichtsfaktoren $W_i$ sind dabei so zu wählen, dass sicher (⇒ bei allen Konstellationen) gilt:
- $${\rm Pr}({\rm Obere\hspace{0.15cm} Schranke}) \ge {\rm Pr}({\rm Blockfehler}) \hspace{0.05cm}. $$
- Eine untere Schranke erfordert zusätzlich die Kenntnis der Gewichtsfunktion $W_i$ für $i = d_{\rm min}$. Damit kann folgende Bedingung erfüllt werden:
- $${\rm Pr}({\rm Untere\hspace{0.15cm} Schranke}) \le {\rm Pr}({\rm Blockfehler}) \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Definition und Eigenschaften von Reed–Solomon–Codes.
- Zu berechnen sind die in der obigen Grafik rot markierten Gewichte $W_i$.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)