Difference between revisions of "Aufgaben:Exercise 2.12Z: Reed-Solomon Syndrome Calculation"
From LNTwww
| Line 2: | Line 2: | ||
[[File:P_ID2559__KC_T_2_5_Darstellung.png|right|frame|$\rm GF(2^3)$ –Umrechnungstabellen]] | [[File:P_ID2559__KC_T_2_5_Darstellung.png|right|frame|$\rm GF(2^3)$ –Umrechnungstabellen]] | ||
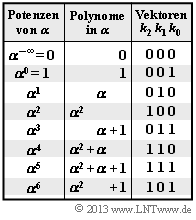
| − | Wie in der [[Aufgabe A2.12]] betrachten wir den Reed–Solomon–Code $(7, \, 4, \, 4)_8$, der auf dem Galoisfeld ${\rm GF}(q)$ mit $q = 8 = 2^3$ basiert. Die Grafik zeigt die zugehörige Umrechnungstabelle. | + | Wie in der [[Aufgabe A2.12]] betrachten wir den Reed–Solomon–Code $(7, \, 4, \, 4)_8$, der auf dem Galoisfeld ${\rm GF}(q)$ mit $q = 8 = 2^3$ basiert. Die Grafik zeigt die zugehörige Umrechnungstabelle. |
| + | |||
| + | Gegeben sind die möglichen Codesymbole in Exponentendarstellung (Potenzen von $\alpha$) sowie in Polynom– und Koeffizientendarstellung. | ||
| + | |||
| + | Vorgegeben ist das Empfangswort $\underline{y} = (\alpha, \, 0, \, alpha^3, \, 0, \, 1, \, \alpha, \, 0)$. Anhand des Syndroms | ||
| + | :$$\underline {s} = (s_0, s_1, s_2) = \underline {y} \cdot { \boldsymbol{\rm H }}^{\rm T}$$ | ||
| + | |||
| + | soll überprüft werden, ob einzelne Symbole des Empfangsvektors $\underline{y}$ bei der Übertragung verfälscht wurden. Gegeben ist hierzu die Prüfmatrix $\mathbf{H}$ des betrachteten Codes und deren Transponierte: | ||
| + | :$${ \boldsymbol{\rm H}} = | ||
| + | \begin{pmatrix} | ||
| + | 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ | ||
| + | 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5}\\ | ||
| + | 1 & \alpha^3 & \alpha^6 & \alpha^2 & \alpha^{5} & \alpha^{1} & \alpha^{4} | ||
| + | \end{pmatrix} \hspace{0.05cm},\hspace{0.4cm} | ||
| + | { \boldsymbol{\rm H}}^{\rm T} = | ||
| + | \begin{pmatrix} | ||
| + | 1 & 1 & 1 \\ | ||
| + | \alpha^1 & \alpha^2 & \alpha^3 \\ | ||
| + | \alpha^2 & \alpha^4 & \alpha^6 \\ | ||
| + | \alpha^3 & \alpha^6 & \alpha^2 \\ | ||
| + | \alpha^4 & \alpha^1 & \alpha^{5} \\ | ||
| + | \alpha^5 & \alpha^{3} & \alpha^{1} \\ | ||
| + | \alpha^6 & \alpha^{5} & \alpha^{4} | ||
| + | \end{pmatrix} \hspace{0.05cm}.$$ | ||
| + | |||
| + | ''Hinweis:'' | ||
| + | * Die Aufgabe bezieht auf die [[Kanalcodierung/Fehlerkorrektur_nach_Reed%E2%80%93Solomon%E2%80%93Codierung#Schritt_.28A.29:_Auswertung_des_Syndroms_beim_BDD| Seite 4]] des Kapitels Fehlercodierung nach Reed–Solomon–Codierung. | ||
Revision as of 11:51, 18 December 2017
Wie in der Aufgabe A2.12 betrachten wir den Reed–Solomon–Code $(7, \, 4, \, 4)_8$, der auf dem Galoisfeld ${\rm GF}(q)$ mit $q = 8 = 2^3$ basiert. Die Grafik zeigt die zugehörige Umrechnungstabelle.
Gegeben sind die möglichen Codesymbole in Exponentendarstellung (Potenzen von $\alpha$) sowie in Polynom– und Koeffizientendarstellung.
Vorgegeben ist das Empfangswort $\underline{y} = (\alpha, \, 0, \, alpha^3, \, 0, \, 1, \, \alpha, \, 0)$. Anhand des Syndroms
- $$\underline {s} = (s_0, s_1, s_2) = \underline {y} \cdot { \boldsymbol{\rm H }}^{\rm T}$$
soll überprüft werden, ob einzelne Symbole des Empfangsvektors $\underline{y}$ bei der Übertragung verfälscht wurden. Gegeben ist hierzu die Prüfmatrix $\mathbf{H}$ des betrachteten Codes und deren Transponierte:
- $${ \boldsymbol{\rm H}} = \begin{pmatrix} 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5}\\ 1 & \alpha^3 & \alpha^6 & \alpha^2 & \alpha^{5} & \alpha^{1} & \alpha^{4} \end{pmatrix} \hspace{0.05cm},\hspace{0.4cm} { \boldsymbol{\rm H}}^{\rm T} = \begin{pmatrix} 1 & 1 & 1 \\ \alpha^1 & \alpha^2 & \alpha^3 \\ \alpha^2 & \alpha^4 & \alpha^6 \\ \alpha^3 & \alpha^6 & \alpha^2 \\ \alpha^4 & \alpha^1 & \alpha^{5} \\ \alpha^5 & \alpha^{3} & \alpha^{1} \\ \alpha^6 & \alpha^{5} & \alpha^{4} \end{pmatrix} \hspace{0.05cm}.$$
Hinweis:
- Die Aufgabe bezieht auf die Seite 4 des Kapitels Fehlercodierung nach Reed–Solomon–Codierung.
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)