Difference between revisions of "Exercise 2.4Z: Repetition to IDFT"
(Die Seite wurde neu angelegt: „{{quiz-Header|Buchseite=Beispiele von Nachrichtensystemen/xDSL als Übertragungstechnik }} [[File:|right|frame|]] ===Fragebogen=== <quiz display=simp…“) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:|right|frame|]] | + | [[File:P_ID1971__Sig_A_5_2.png|right|frame|Mustersätze zur IDFT]] |
| + | Bei der Diskreten Fouriertransformation (DFT) werden aus den Zeitabtastwerten $d(\nu) \ {\rm mit} \ \nu = 0, ... , N – 1$ die diskreten Spektralkoeffizienten $D(\mu) \ {\rm mit} \ \mu = 0, ... , N – 1$ wie folgt berechnet: | ||
| + | :$$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} d(\nu)\cdot {w}^{\hspace{0.05cm}\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$ | ||
| + | Hierbei ist mit $w$ der komplexe Drehfaktor abgekürzt, der folgendermaßen definiert ist: | ||
| + | :$$w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} = \cos \left( \frac {2 \pi}{N}\right)-{\rm j} \cdot \sin \left( \frac {2 \pi}{N}\right) \hspace{0.05cm}.$$ | ||
| + | Somit gilt für die Inverse Diskrete Fouriertransformation (IDFT) als Umkehrfunktion der DFT: | ||
| + | :$$ d(\nu) = \sum_{\mu = 0 }^{N-1} D(\mu) \cdot {w}^{-\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$ | ||
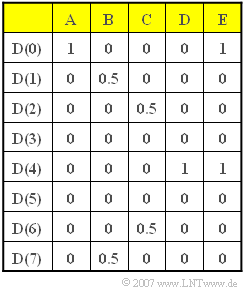
| + | In dieser Aufgabe sollen für verschiedene Beispielfolgen $D(\mu)$ – die in obiger Tabelle mit „A”, ... , „E” bezeichnet sind – die Zeitkoeffizienten $d(\nu)$ ermittelt werden. Es gilt somit stets $N = 8$. | ||
| + | ''Hinweis:'' | ||
| + | Die Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel [[Beispiele_von_Nachrichtensystemen/Verfahren_zur_Senkung_der_Bitfehlerrate_bei_DSL#Gain_Scaling_und_Tone_Ordering|Gain Scaling und Tone Ordering]] des Buches „Signaldarstellung” und ist identisch mit der dortigen Aufgabe A5.2. Sie können sich die Lösung auch mit folgendem Interaktionsmodul verdeutlichen: | ||
| + | |||
| + | Diskrete Fouriertransformation | ||
| + | |||
| + | DFT und IDFT spielen auch bei [[Beispiele_von_Nachrichtensystemen/xDSL_als_Übertragungstechnik#DMT.E2.80.93Realisierung_mit_IDFT.2FDFT|DSM/DSL]] eine große Rolle. Im entsprechenden Kapitel werden die Spektralkoeffizienten allerdings mit $D_k$ bezeichnet und die Zeitabtastwerte mit $s_l$. Wir bitten Sie, diese Nomenklaturdiskrepanz zu entschuldigen. | ||
| + | Für die beiden Laufvariablen gelten mit dem DFT–Parameter $N = 8$: | ||
| + | :$$0 \le k \le 7, \hspace{0.2cm}0 \le l \le 7 \hspace{0.05cm}.$$ | ||
Revision as of 16:32, 18 December 2017
Bei der Diskreten Fouriertransformation (DFT) werden aus den Zeitabtastwerten $d(\nu) \ {\rm mit} \ \nu = 0, ... , N – 1$ die diskreten Spektralkoeffizienten $D(\mu) \ {\rm mit} \ \mu = 0, ... , N – 1$ wie folgt berechnet:
- $$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} d(\nu)\cdot {w}^{\hspace{0.05cm}\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$
Hierbei ist mit $w$ der komplexe Drehfaktor abgekürzt, der folgendermaßen definiert ist:
- $$w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} = \cos \left( \frac {2 \pi}{N}\right)-{\rm j} \cdot \sin \left( \frac {2 \pi}{N}\right) \hspace{0.05cm}.$$
Somit gilt für die Inverse Diskrete Fouriertransformation (IDFT) als Umkehrfunktion der DFT:
- $$ d(\nu) = \sum_{\mu = 0 }^{N-1} D(\mu) \cdot {w}^{-\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$
In dieser Aufgabe sollen für verschiedene Beispielfolgen $D(\mu)$ – die in obiger Tabelle mit „A”, ... , „E” bezeichnet sind – die Zeitkoeffizienten $d(\nu)$ ermittelt werden. Es gilt somit stets $N = 8$.
Hinweis: Die Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel Gain Scaling und Tone Ordering des Buches „Signaldarstellung” und ist identisch mit der dortigen Aufgabe A5.2. Sie können sich die Lösung auch mit folgendem Interaktionsmodul verdeutlichen:
Diskrete Fouriertransformation
DFT und IDFT spielen auch bei DSM/DSL eine große Rolle. Im entsprechenden Kapitel werden die Spektralkoeffizienten allerdings mit $D_k$ bezeichnet und die Zeitabtastwerte mit $s_l$. Wir bitten Sie, diese Nomenklaturdiskrepanz zu entschuldigen. Für die beiden Laufvariablen gelten mit dem DFT–Parameter $N = 8$:
- $$0 \le k \le 7, \hspace{0.2cm}0 \le l \le 7 \hspace{0.05cm}.$$
Fragebogen
Musterlösung