Difference between revisions of "Aufgaben:Exercise 1.4: AMI and MMS43 Code"
| Line 35: | Line 35: | ||
$r_{\rm AMI} \ = \ $ { 36.9 3% } $\ \%$ | $r_{\rm AMI} \ = \ $ { 36.9 3% } $\ \%$ | ||
| − | {Es gelte $s_{0} = 0.75 \ {\rm V} und R = 100 \ {\rm Ω}$. Wie groß ist die mittlere Sendeleistung? | + | {Es gelte $s_{0} = 0.75 \ {\rm V}$ und $R = 100 \ {\rm Ω}$. Wie groß ist die mittlere Sendeleistung? |
|type="{}"} | |type="{}"} | ||
$P_{\rm S, \ AMI} \ = \ $ { 2.8 3% } $\ \rm mW$ | $P_{\rm S, \ AMI} \ = \ $ { 2.8 3% } $\ \rm mW$ | ||
| Line 47: | Line 47: | ||
{Wie groß ist die Redundanz des MMS43–Codes? | {Wie groß ist die Redundanz des MMS43–Codes? | ||
|type="{}"} | |type="{}"} | ||
| − | $r_{\rm MMS43} \ = \ $ { 15.9 | + | $r_{\rm MMS43} \ = \ $ { 15.9 3% } $\ \%$ |
{Wie groß ist die Symbolrate auf dem $\rm U_{\rm K0}$–Bus, wenn pro Millisekunde 12 ternäre Synchronisations– und Steuersymbole zu berücksichtigen sind? | {Wie groß ist die Symbolrate auf dem $\rm U_{\rm K0}$–Bus, wenn pro Millisekunde 12 ternäre Synchronisations– und Steuersymbole zu berücksichtigen sind? | ||
| Line 53: | Line 53: | ||
$R_{\rm U_{K0}} \ = \ $ { 120000 3% } $\ \rm Ternärsymbole/Sekunde$ | $R_{\rm U_{K0}} \ = \ $ { 120000 3% } $\ \rm Ternärsymbole/Sekunde$ | ||
| − | {Es gelte $s_{0} = 2.5 \ {\rm V} und R = 100 \ {\rm \Omega }$. Wie groß ist die Sendeleistung? ''Hinweis:'' Gehen Sie von gleichwahrscheinlichen Ternärsymbolen aus. | + | {Es gelte $s_{0} = 2.5 \ {\rm V}$ und $R = 100 \ {\rm \Omega }$. Wie groß ist die Sendeleistung? ''Hinweis:'' Gehen Sie von gleichwahrscheinlichen Ternärsymbolen aus. |
|type="{}"} | |type="{}"} | ||
$P_{\rm S,\ MMS43} \ = \ $ { 4.2 3% } $\ \rm mW$ | $P_{\rm S,\ MMS43} \ = \ $ { 4.2 3% } $\ \rm mW$ | ||
Revision as of 11:20, 19 December 2017
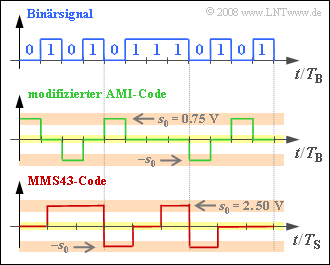
Bei ISDN werden zwei verschiedene ternäre Übertragungscodes eingesetzt, die in der Grafik an einem beispielhaften binären Eingangssignal verdeutlicht werden sollen. Im oberen Diagramm sind 12 Bit (jeweils mit der Bitdauer $T_{\rm B}$) dargestellt.
- Auf der $\rm S_{0}$–Schnittstelle (zwischen NTBA und Endgerät) verwendet man wird den modifizierten AMI–Code. Der Unterschied zum herkömmlichen AMI–Code ist die Vertauschung $0 \Leftrightarrow 1$ des binären Eingangssignals.
- Dagegen wird auf der $\rm U_{K0}$–Schnittstelle der MMS43–Code (Modified Monitoring Sum 4B3T) eingesetzt, wobei jeweils 4 Binärsymbole durch 3 Ternärsymbole (Spannungswerte $0 \ {\rm V}, +2.5 \ {\rm V}$ und $-2.5 \ {\rm V}$) ersetzt werden. Die Zuordnung erfolgt abhängig von den vorher codierten Symbolen.
Hinweise:
- Die Aufgabe gehört zum Kapitel ISDN-Basisanschluss.
- Angaben zum MMS43–Code finden Sie im Kapitel Blockweise Codierung mit 4B3T-Codes des Buches „Digitalsignalübertragung” und zum AMI–Code im Kapitel Symbolweise Codierung mit Pseudoternärcodes des gleichen Buches.
Fragebogen
Musterlösung
(1) Richtig sind die zwei ersten Aussagen. Der modifizierte AMI–Code ist ein sog. Pseudo–Ternärcode mit $T_{\rm S} = T_{\rm B}$ und symbolweiser Codierung. Die angegebenen Zuordnungen gelten für den herkömmlichen AMI–Code. Dagegen wird beim modifizierten AMI–Code die binäre „$1$” durch den Spannungswert $0 \ \rm V$ repräsentiert und die binäre „$0$” alternierend durch $+s_{0}$ bzw. $–s_{0}$, wobei für $s_{0} = 0.75 \ \rm V$ zu setzen ist.
(1) Richtig sind die zwei ersten Aussagen. Der modifizierte AMI–Code ist ein sog. Pseudo–Ternärcode mit $T_{\rm S} = T_{\rm B}$ und symbolweiser Codierung. Die angegebenen Zuordnungen gelten für den herkömmlichen AMI–Code. Dagegen wird beim modifizierten AMI–Code die binäre „$1$” durch den Spannungswert $0 \ \rm V$ repräsentiert und die binäre „$0$” alternierend durch $+s_{0}$ bzw. $–s_{0}$, wobei für $s_{0} = 0.75 \ \rm V$ zu setzen ist.
(2) Die äquivalente Bitrate des AMI–codierten Signals beträgt $R_{\rm C} = {\rm ld}(3)/T_{\rm S}$, während die Bitrate des redundanzfreien binären Quellensignals gleich $R_{\rm B} = 1/T_{\rm B}$ ist. Mit $T_{\rm S} = T_{\rm B}$ erhält man entsprechend dem Grundlagen der codierten Übertragung des Buches „Digitalsignalübertragung” für die (relative) Redundanz des modifizierten AMI–Codes:
- $$r_{\rm AMI} = \frac{R_{\rm C}-R_{\rm B}}{R_{\rm C}} = 1 - \frac{1}{{\rm ld}\,(3)} \hspace{0.15cm}\underline{\approx 36.9\,\%} \hspace{0.05cm}.$$
(3) Unter Verwendung des Einheitswiderstandes $R = 1 \ \rm \Omega $ gilt für die Sendeleistung (mit der Einheit $\rm V^{2}$):
- $$P_{\rm S,\,AMI} = {1}/{2} \cdot {s_0}^2 = {1}/{2} \cdot {0.75\,{\rm V}}^2 \approx 0.28\,{\rm V^2} \hspace{0.05cm}.$$
Hierbei ist berücksichtigt, dass das AMI–codierte Signal in der Hälfte der Zeit gleich $0 \ \rm V$ ist. Bei Berücksichtigung des Widerstandes $R = 100 \ \rm \Omega$ ergibt sich schließlich:
- $$P_{\rm S,\,AMI} = \frac{0.28\,{\rm V^2}}{100\,\Omega} \hspace{0.15cm}\underline{ = 2.8\,{\rm mW}} \hspace{0.05cm}.$$
(4) Der MMS43–Code arbeitet tatsächlich blockweise, wobei $m_{q} = 4 \ \rm Binärsymbole$ durch $m_{c} = 3 \ \rm Ternärsymbole$ ersetzt werden:
- $$4 \cdot T_{\rm B} = 3 \cdot T_{\rm S}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} T_{\rm S} = {4}/{3} \cdot T_{\rm B} \hspace{0.05cm}.$$
Das heißt: Der erste Lösungsvorschlag trifft nicht zu ebenso wie der letzte. Richtig ist der Vorschlag 2. Bei Blockcodierung kann das Binärsymbol „$0$” nicht einheitlich durch das gleiche Codesymbol ersetzt werden. Vielmehr lässt sich die Codierung wie folgt beschreiben, wenn man zu Beginn von der laufenden digitalen Summe $\Sigma_{0} = 0$ ausgeht (siehe Grafik auf der Angabenseite):
- $$\mathbf{0 1 0 1} \hspace{0.1cm} \ \Rightarrow \ \hspace{0.1cm}\mathbf{0 + +}\hspace{0.2cm}({\it \Sigma}_1 = 2)\hspace{0.05cm},$$
- $$ \mathbf{0 1 1 1} \hspace{0.1cm} \ \Rightarrow \ \hspace{0.1cm}\mathbf{- \,0 \,\,+}\hspace{0.2cm}({\it \Sigma}_2 = 2)\hspace{0.05cm},$$
- $$ \mathbf{0 1 0 1} \hspace{0.1cm} \ \Rightarrow \ \hspace{0.1cm}\mathbf{- \,0\,\,\, 0}\hspace{0.2cm}({\it \Sigma}_3 = 1) \hspace{0.05cm}.$$
In der Aufgabe 1.4Z wird der MMS43–Code noch ausführlicher behandelt.
(5) Der MMS43–Code gehört zur Klasse der 4B3T–Codes. Für diesen gilt:
- $$R_{\rm B} = \frac{1}{T_{\rm B}}, \hspace{0.2cm} R_{\rm C} = \frac{{\rm ld}\,(3)}{T_{\rm S}}$$
- $$\Rightarrow \hspace{0.3cm}r_{\rm MMS43} = 1 - \frac{R_{\rm B}}{R_{\rm C}} = 1 - \frac{T_{\rm S}/T_{\rm B}}{{\rm ld}\,(3)} = 1 - \frac{4/3}{{\rm ld}\,(3)} \hspace{0.15cm}\underline{\approx 15.9\,\%} \hspace{0.05cm}.$$
(6) Pro Millisekunde werden auf dem $U_{K0}$–Bus die folgende Anzahl an Ternärsymbolen übertragen:
- Kanal B1: $64 \ {\rm Binärsymbole} \Rightarrow 48 \ {\rm Ternärsymbole}$,
- Kanal B2: $64 \ {\rm Binärsymbole} \Rightarrow 48 \ {\rm Ternärsymbole}$,
- D–Kanal: $16 \ {\rm Binärsymbole} \Rightarrow 12 \ {\rm Ternärsymbole}$,
- Synchronisations– und Steuersymbole $\Rightarrow 12 \ {\rm Ternärsymbole}$.
Dies ergibt als Summe $120$ Ternärsymbole pro Millisekunde bzw. 120 000 Ternärsymbole pro Sekunde.
(7) Unter Berücksichtigung des Hinweises auf der Angabenseite und der gegenüber dem (modifizierten) AMI–Code größeren Sendeamplitude $s_{0} = 2.5 \ \rm V$ erhält man:
- $$P_{\rm S,\,MMS43} = \frac{2}{3} \cdot \frac{{s_0}^2}{R} = \frac{2}{3} \cdot \frac{({2.5\,{\rm V}})^2}{100\,{\rm \Omega}} \hspace{0.15cm}\underline{\approx 4.2\,{\rm mW}} \hspace{0.05cm}.$$