Aufgaben:Exercise 2.16: Bounded Distance Decoding: Decision Regions

• Return to book

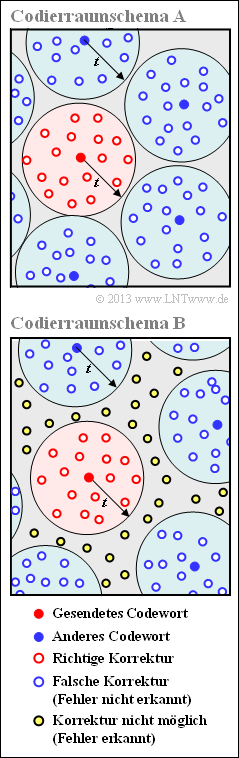
Wir gehen von einem Blockcode der Länge $n$ mit Symbolen $c_i ∈ {\rm GF}(2^m)$ aus, der bis zu $t$ Symbole korrigieren kann. Jedes mögliche Empfangswort $\underline{y}_i$ kann dann als ein Punkt in einem hochdimensionalen Raum angesehen werden. Geht man von der Basis ${\rm GF}(2) = \{0, \, 1\}$ aus, so beträgt die Dimension $n \cdot m$.

Die Grafik zeigt einen solchen Raum in stark vereinfachender 2D–Darstellung. Die Abbildung ist wie folgt zu interpretieren:

• Gesendet wurde der rote Punkt $\underline{c}_j$. Alle rot umrandeten Punkte $\underline{y}_i$ in einer Hyperkugel um diesen Punkt $\underline{c}_j$ mit dem Parameter $t$ als Radius können korrigiert werden. Mit der Nomenklatur gemäß der Grafik im Theorieteil gilt dann $\underline{z}_i = \underline{c}_j$  ⇒  „Die Fehlerkorrektur ist erfolgreich”.

• Bei sehr vielen Symbolfehlern kann $\underline{c}_j$ in einen blauen (oder weißblauen) Punkt $\underline{y}_j$ verfälscht werden, der zur Hyperkugel eines anderen Codewortes $\underline{c}_{k ≠ j}$ gehört. In diesem Fall trifft der Decoder eine falsche Entscheidung  ⇒  „Das Empfangswort $\underline{y}_j$ wird falsch decodiert”.

• Schließlich kann es wie in der unteren Skizze auch noch gelbe Punkte geben, die zu keiner Hyperkugel gehören  ⇒  „Das Empfangswort $\underline{y}_j$ ist nicht decodierbar”.

In dieser Aufgabe sollen Sie entscheiden, welches der beiden Coderaumschemata geeignet ist zur Beschreibung der

• BDD–Decodierung von Hamming–Codes bzw.
• BDD–Decodierung von Reed–Solomon–Codes.

Hinweis:

• Die Aufgabe ergänzt die Thematik des Kapitels Fehlerwahrscheinlichkeit und Anwendungsgebiete und soll signifikante Unterschiede bei der Decodierung von Reed–Solomon–Codes und Hamming–Codes verdeutlichen.

Fragebogen

1

Welches Codierraumschema trifft für die Hamming–Codes zu?

	Codierraumschema A,
	Codierraumschema B.

2

Welche Aussage gilt für die Wahrscheinlichkeit, dass bei Hamming–Codierung ein Empfangswort $\underline{y}$ nicht decodiert werden kann?

	Die Wahrscheinlichkeit ${\rm Pr}(\underline{y} \rm \ ist \ nicht \ decodierbar)$ ist exakt $0$.
	${\rm Pr}(\underline{y} \rm \ ist \ nicht \ decodierbar)$ ist ungleich $0$, aber vernachlässigbar.
	Es gilt ${\rm Pr}(\underline{y} {\rm \ ist \ nicht \ decodierbar}) > {\rm Pr}(\underline{y} \rm \ wird \ falsch \ decodiert)$.

3

Welches Codierraumschema trifft für die Reed–Solomon–Codes zu?

	Codierraumschema A,
	Codierraumschema B.

4

Welche Aussage gilt für die Wahrscheinlichkeit, dass ein Empfangswort $\underline{y}$ nach Reed–Solomon–Codierung nicht decodiert werden kann?

	Die Wahrscheinlichkeit ${\rm Pr}(\underline{y} \rm \ ist \ nicht \ decodierbar)$ ist exakt $0$.
	${\rm Pr}(\underline{y} \rm \ ist \ nicht \ decodierbar)$ ist ungleich $0$, aber vernachlässigbar.
	Es gilt ${\rm Pr}(\underline{y} {\rm \ ist \ nicht \ decodierbar}) > {\rm Pr}(\underline{y} \rm \ wird \ falsch \ decodiert)$.

Musterlösung

Solution

(1)  Das Codierraumschema A beschreibt einen perfekten Code. Da jeder Hamming–Code $(n, \, k, \, 3)$ ein perfekter Code ist, gilt Antwort 1. Bei diesen gibt es insgesamt $2^n$ mögliche Empfangsworte $\underline{y}_i$, die bei der Syndromdecodierung einem von $2^k$ möglichen Codeworten $\underline{c}_j$ zugeordnet werden. Aufgrund der HC–Eigenschaft $d_{\rm min} = 3$ haben alle Kugeln im $n$–dimensionalen Raum den Radius $t = 1$. In allen Kugeln gibt es somit $2^{n-k}$ Punkte, zum Beispiel

• HC (7, 4, 3): Einen Punkt für die fehlerfreie Übertragung und sieben Punkte für einen Bitfehler  ⇒  $1 + 7 = 8 = 2^3 = 2^{7-4}$.
• HC (15, 11, 3): Auch hier wieder einen Punkt für die fehlerfreie Übertragung und nun 15 Punkte für einen Bitfehler  ⇒  $1 + 15 = 16 = 2^4 = 2^{15-11}$.

Hinweis: Da der Hamming–Code ein Binärcode ist, hat hier der Coderaum die Dimension $n$.

(2)  Richtig ist Antwort 1. Im grauen Bereich außerhalb von „Kugeln” gibt es bei einem perfekten Code keinen einzigen Punkt, wie die Rechnung zur Teilaufgabe (1) gezeigt hat.

(3)  Die Reed–Solomon–Codes werden durch das Codierraumschema B beschrieben  ⇒  Antwort 2. Hier gibt es zahlreiche gelbe Punkte im grauen Bereich, also Punkte die bei Bounded Distance Decoding (BDD) keiner Kugel zugeordnet werden können.

Betrachten wir beispielweise den $\rm RSC \, (7, \, 3, \, 5)_8$ mit den Codeparametern $n = 7, \, k = 3$ und $t = 2$, so gibt es hier insgesamt $8^7 = 2097152$ Punkte und $8^3 = 512$ Hyperkugeln. Wäre dieser Code perfekt, so müsste es also innerhalb jeder Kugel $8^4 = 4096$ Punkte geben. Es gilt aber:

$${\rm Pr(\underline{\it y}_{\it i} \hspace{0.15cm}liegt\hspace{0.15cm} innerhalb\hspace{0.15cm} der\hspace{0.15cm} roten\hspace{0.15cm} Kugel)} = {\rm Pr}(f \le t) =$$

$$= {\rm Pr}(f = 0)+ {\rm Pr}(f = 1)+{\rm Pr}(f = 2) =1 + {7 \choose 1} \cdot 7 + {7 \choose 2} \cdot 7^2 = 1079 \hspace{0.05cm}.$$

Für ${\rm Pr}(f = 1)$ ist berücksichtigt, dass es „$7 \rm \ über \ 1$” $= 7$ Fehlerpositionen geben kann, und für jede Fehlerposition auch 7 unterschiedliche Fehlerwerte. Entsprechendes ist auch für ${\rm Pr}(f = 2)$ berücksichtigt.

(4)  Richtig ist hier die Antwort 3. Ein Punkt im grauen Niemandsland wird mit weniger Symbolfehlern erreicht als ein Punkt in einer anderen Hyperkugel. für lange Codes wird in der Literatur eine obere Schranke für die Verfälschungswahrscheinlichkeit angegeben:

$${\rm Pr(\underline{\it y}_{\it i} \hspace{0.15cm}wird\hspace{0.15cm} falsch\hspace{0.15cm} decodiert)} = {\rm Pr}(\underline{z} \ne \underline{c}) \le \frac{1}{t\hspace{0.05cm}!} \hspace{0.05cm}.$$

Für den $\rm RSC \, (225, \, 223, \, 33)_{256} \ \Rightarrow \ t = 16$ liefert diese obere Schranke den Wert $1/(16!) < 10^{-14}$.