Difference between revisions of "Aufgaben:Exercise 2.5: Half-Wave Rectification"
m (Guenter verschob die Seite 2.5 Einweggleichrichtung nach Aufgabe 2.5: Einweggleichrichtung) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID311__Sig_A_2_5.png|right| | + | [[File:P_ID311__Sig_A_2_5.png|right|frame|Gleichgerichtete Cosinusfunktionen]] |
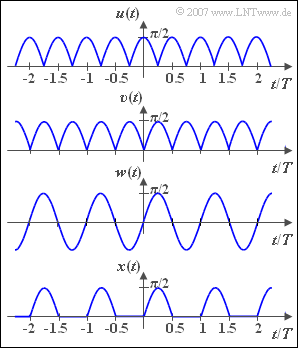
Gesucht sind die Fourierkoeffizienten des unten skizzierten Signals $x(t)$, das sich durch die Einweggleichrichtung des Sinussignals $w(t)$ mit der Amplitude $\pi /2$ ergibt. | Gesucht sind die Fourierkoeffizienten des unten skizzierten Signals $x(t)$, das sich durch die Einweggleichrichtung des Sinussignals $w(t)$ mit der Amplitude $\pi /2$ ergibt. | ||
| Line 29: | Line 29: | ||
:$$A_2=2/3; \;A_4=-2/15;\;A_6=2/35;\;A_8=-2/63.$$ | :$$A_2=2/3; \;A_4=-2/15;\;A_6=2/35;\;A_8=-2/63.$$ | ||
| + | |||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
*Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Fourierreihe|Fourierreihe]]. | *Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Fourierreihe|Fourierreihe]]. | ||
| − | *Eine kompakte Zusammenfassung der Thematik finden Sie in den beiden Lernvideos [[Zur Berechnung der Fourierkoeffizienten]] sowie [[Eigenschaften | + | *Eine kompakte Zusammenfassung der Thematik finden Sie in den beiden Lernvideos |
| + | :[[Zur_Berechnung_der_Fourierkoeffizienten_(Lernvideo)|Zur Berechnung der Fourierkoeffizienten]] sowie [[Eigenschaften_der_Fourierreihendarstellung_(Lernvideo)|Eigenschaften der Fourierreihendarstellung]]. | ||
*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| Line 40: | Line 44: | ||
{Berechnen Sie die Fourierkoeffizienten des Signals $v(t)$. Welchen Wert besitzt der Koeffizient $A_2$? | {Berechnen Sie die Fourierkoeffizienten des Signals $v(t)$. Welchen Wert besitzt der Koeffizient $A_2$? | ||
|type="{}"} | |type="{}"} | ||
| − | + | $A_2\ = \ $ { -0.67--0.66 } | |
{Berechnen Sie die Fourierkoeffizienten des Signals $w(t)$. Welchen Wert besitzt der Koeffizient $B_1$? | {Berechnen Sie die Fourierkoeffizienten des Signals $w(t)$. Welchen Wert besitzt der Koeffizient $B_1$? | ||
|type="{}"} | |type="{}"} | ||
| − | + | $B_1\ = \ $ { 1.571 3% } | |
{Wie kann $x(t)$ aus $v(t)$ und $w(t)$ zusammengesetzt werden? Geben Sie die entsprechenden Fourierkoeffizienten des Signals $x(t)$ an, insbesondere | {Wie kann $x(t)$ aus $v(t)$ und $w(t)$ zusammengesetzt werden? Geben Sie die entsprechenden Fourierkoeffizienten des Signals $x(t)$ an, insbesondere | ||
|type="{}"} | |type="{}"} | ||
| − | + | $A_0\ = \ $ { 0.5 3% } | |
| − | $B_1$ | + | $B_1\ = \ $ { 0.785 3% } |
| − | $A_2$ | + | $A_2\ = \ $ { -0.34--0.33 } |
</quiz> | </quiz> | ||
| Line 56: | Line 60: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Auch das verschobene Signal $v(t)$ ist gerade und alle Sinuskoeffizienten sind dementsprechend $0$. Am Gleichsignalkoeffizienten ändert sich ebenfalls nichts: $A_0 = 1$. |
Aus den Signalverläufen ist zu erkennen, dass $v(t) = u(t – T/4)$ gilt: | Aus den Signalverläufen ist zu erkennen, dass $v(t) = u(t – T/4)$ gilt: | ||
| − | $$v(t)=1+\frac{2}{3}\cdot \cos(2\omega_0(t-\frac{T}{4}))-\frac{2}{15}\cdot \cos(4\omega_0(t-\frac{T}{4}))+\frac{2}{35}\cdot \cos(6\omega_0(t-\frac{T}{4}))-\dots$$ | + | :$$v(t)=1+\frac{2}{3}\cdot \cos(2\omega_0(t-\frac{T}{4}))-\frac{2}{15}\cdot \cos(4\omega_0(t-\frac{T}{4}))+\frac{2}{35}\cdot \cos(6\omega_0(t-\frac{T}{4}))-\dots$$ |
Die Cosinusterme können nun mit $\omega_0 \cdot T = 2 \pi$ umgeformt werden: | Die Cosinusterme können nun mit $\omega_0 \cdot T = 2 \pi$ umgeformt werden: | ||
| − | $$\cos(2\omega_0(t-\frac{T}{4}))=\cos(2\omega_0t-\pi)=-\cos(2\omega_0t),$$ | + | :$$\cos(2\omega_0(t-\frac{T}{4}))=\cos(2\omega_0t-\pi)=-\cos(2\omega_0t),$$ |
| − | $$\cos(4\omega_0(t-\frac{T}{4}))=\cos(4\omega_0t-2\pi)=\cos(4\omega_0t),$$ | + | :$$\cos(4\omega_0(t-\frac{T}{4}))=\cos(4\omega_0t-2\pi)=\cos(4\omega_0t),$$ |
| − | $$\cos(6\omega_0(t-\frac{T}{4}))=\cos(6\omega_0t-3\pi)=-\cos(6\omega_0t).$$ | + | :$$\cos(6\omega_0(t-\frac{T}{4}))=\cos(6\omega_0t-3\pi)=-\cos(6\omega_0t).$$ |
Damit erhält man für die Fourierreihe: | Damit erhält man für die Fourierreihe: | ||
| − | $$v(t)=1-{2}/{3}\cdot \cos(2\omega_0t)-{2}/{15}\cdot \cos(4\omega_0t)-{2}/{35}\cdot \cos(6\omega_0t)-\dots$$ | + | :$$v(t)=1-{2}/{3}\cdot \cos(2\omega_0t)-{2}/{15}\cdot \cos(4\omega_0t)-{2}/{35}\cdot \cos(6\omega_0t)-\dots$$ |
bzw. für die Cosinuskoeffizienten mit geradzahligem $n$: | bzw. für die Cosinuskoeffizienten mit geradzahligem $n$: | ||
| − | $$A_n=\frac{-2}{n^2-1}\hspace{0.5cm}\Rightarrow\hspace{0.5cm}A_2 \hspace{0.1cm}\underline{= –\hspace{-0.1cm}2/3}.$$ | + | :$$A_n=\frac{-2}{n^2-1}\hspace{0.5cm}\Rightarrow\hspace{0.5cm}A_2 \hspace{0.1cm}\underline{= –\hspace{-0.1cm}2/3}.$$ |
| − | '''2 | + | '''(2)''' Wegen $w(t) = \pi /2 \cdot \sin(\omega_0 t)$ sind alle Fourierkoeffizienten außer $B_1 = \pi /2 \hspace{0.1cm}\underline{=1.571}$ gleich $0$. |
| − | '''3 | + | '''(3)''' Aus der grafischen Darstellung erkennt man den Zusammenhang $x(t)={1}/{2} \cdot [v(t)+w(t)].$ Das bedeutet: |
| − | $$x(t)=\frac{1}{2}+\frac{\pi}{4}\cdot \sin(\omega_0 t)-\frac{1}{3}\cdot \cos(2\omega_0 t)-\frac{1}{15}\cdot \cos(4\omega_0 t)-\frac{1}{35}\cdot \cos(6\omega_0 t)-\ldots$$ | + | :$$x(t)=\frac{1}{2}+\frac{\pi}{4}\cdot \sin(\omega_0 t)-\frac{1}{3}\cdot \cos(2\omega_0 t)-\frac{1}{15}\cdot \cos(4\omega_0 t)-\frac{1}{35}\cdot \cos(6\omega_0 t)-\ldots$$ |
| − | Die gesuchten Fourierkoeffizienten sind somit $A_0 \hspace{0.1cm}\underline{=1/2}$; $B_1 = \pi /4 \hspace{0.1cm}\underline{= 0.785}$ und $A_2\hspace{0.1cm}\underline{ = | + | Die gesuchten Fourierkoeffizienten sind somit $A_0 \hspace{0.1cm}\underline{=1/2}$; $B_1 = \pi /4 \hspace{0.1cm}\underline{= 0.785}$ und :$A_2\hspace{0.1cm}\underline{ = -1/3}$. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
[[Category:Aufgaben zu Signaldarstellung|^2. Periodische Signale^]] | [[Category:Aufgaben zu Signaldarstellung|^2. Periodische Signale^]] | ||
Revision as of 12:04, 20 December 2017
Gesucht sind die Fourierkoeffizienten des unten skizzierten Signals $x(t)$, das sich durch die Einweggleichrichtung des Sinussignals $w(t)$ mit der Amplitude $\pi /2$ ergibt.
Als bekannt vorausgesetzt wird die Fourierreihendarstellung des oben skizzierten Signals $u(t)$. Diese wurde bereits in der Aufgabe 2.4 ermittelt. Unter Berücksichtigung der Amplitude $\pi /2$ gilt hierfür:
- $$u(t)=1+\frac{2}{3} \cdot \cos(\omega_1t)-\frac{2}{15}\cdot \cos(2\omega_1t)+\frac{2}{35}\cdot \cos(3\omega_1t)-\dots$$
Anzumerken ist:
- Die Grundkreisfrequenz ist mit $\omega_1$ bezeichnet. Da aber die Periodendauer der Signale $u(t)$ und $v(t)$ jeweils $T/2$ beträgt, gilt $\omega_1 = 2\pi /(T/2) = 4 \pi /T$.
- Weil in dieser Aufgabe die Signale $u(t)$, $w(t)$ und $x(t)$ zueinander in Bezug gebracht werden sollen, muss auch das Signal $u(t)$ mit der Periodendauer $T$ des Signals $x(t)$ dargestellt werden. Mit $\omega_0 = 2\pi /T = \omega_1/2$ gilt somit gleichermaßen:
- $$u(t)=1+\frac{2}{3} \cdot \cos(2\omega_0t)-\frac{2}{15} \cdot \cos(4\omega_0t)+\frac{2}{35} \cdot \cos(6\omega_0t)-\dots$$
Für die Fourierkoeffizienten bedeutet dies:
- der Gleichkoeffizient ergibt sich zu $A_0 = 1$,
- alle Sinuskoeffizienten sind $B_n = 0$,
- die Cosinuskoeffizienten mit ungeradzahligem $n = 1, 3, 5, ...$ sind alle $0$,
- die Cosinuskoeffizienten mit geradzahligem $n = 2, 4, 6, ...$ sind ungleich $0$:
- $$A_n=(-1)^{\hspace{0.01cm}n/2+1}\frac{2}{n^2-1}.$$
Daraus ergeben sich folgende Zahlenwerte:
- $$A_1=A_3=A_5=\dots=0,$$
- $$A_2=2/3; \;A_4=-2/15;\;A_6=2/35;\;A_8=-2/63.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Fourierreihe.
- Eine kompakte Zusammenfassung der Thematik finden Sie in den beiden Lernvideos
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
- $$v(t)=1+\frac{2}{3}\cdot \cos(2\omega_0(t-\frac{T}{4}))-\frac{2}{15}\cdot \cos(4\omega_0(t-\frac{T}{4}))+\frac{2}{35}\cdot \cos(6\omega_0(t-\frac{T}{4}))-\dots$$
Die Cosinusterme können nun mit $\omega_0 \cdot T = 2 \pi$ umgeformt werden:
- $$\cos(2\omega_0(t-\frac{T}{4}))=\cos(2\omega_0t-\pi)=-\cos(2\omega_0t),$$
- $$\cos(4\omega_0(t-\frac{T}{4}))=\cos(4\omega_0t-2\pi)=\cos(4\omega_0t),$$
- $$\cos(6\omega_0(t-\frac{T}{4}))=\cos(6\omega_0t-3\pi)=-\cos(6\omega_0t).$$
Damit erhält man für die Fourierreihe:
- $$v(t)=1-{2}/{3}\cdot \cos(2\omega_0t)-{2}/{15}\cdot \cos(4\omega_0t)-{2}/{35}\cdot \cos(6\omega_0t)-\dots$$
bzw. für die Cosinuskoeffizienten mit geradzahligem $n$:
- $$A_n=\frac{-2}{n^2-1}\hspace{0.5cm}\Rightarrow\hspace{0.5cm}A_2 \hspace{0.1cm}\underline{= –\hspace{-0.1cm}2/3}.$$
(2) Wegen $w(t) = \pi /2 \cdot \sin(\omega_0 t)$ sind alle Fourierkoeffizienten außer $B_1 = \pi /2 \hspace{0.1cm}\underline{=1.571}$ gleich $0$.
(3) Aus der grafischen Darstellung erkennt man den Zusammenhang $x(t)={1}/{2} \cdot [v(t)+w(t)].$ Das bedeutet:
- $$x(t)=\frac{1}{2}+\frac{\pi}{4}\cdot \sin(\omega_0 t)-\frac{1}{3}\cdot \cos(2\omega_0 t)-\frac{1}{15}\cdot \cos(4\omega_0 t)-\frac{1}{35}\cdot \cos(6\omega_0 t)-\ldots$$
Die gesuchten Fourierkoeffizienten sind somit $A_0 \hspace{0.1cm}\underline{=1/2}$; $B_1 = \pi /4 \hspace{0.1cm}\underline{= 0.785}$ und :$A_2\hspace{0.1cm}\underline{ = -1/3}$.