Aufgaben:Exercise 3.8Z: Convolution of Two Rectangles

• Return to book

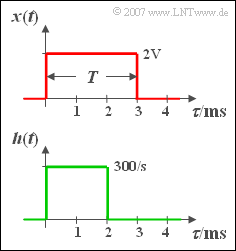
Am Eingang eines kausalen LZI-Systems (also linear und zeitinvariant) mit einer rechteckförmigen Impulsantwort ${h(t)}$ der Dauer $2 \,\text{ms}$ liegt ein Rechteckimpuls ${x(t)}$ der Dauer $T = 3 \,\text{ms}$ und der Amplitude $A = 2\,\text{ V}$ an. Die beiden Rechteckfunktionen beginnen jeweils zum Zeitpunkt $t = 0$.

In dieser Aufgabe sollen Sie das Ausgangssignal ${y(t)}$ mit Hilfe der grafischen Faltung berechnen. Wie man leicht nachprüfen kann, ist das Ausgangssignal ${y(t)}$

• nur im Bereich von $0$ bis $5 \text{ms}$ von Null verschieden,
• symmetrisch zum Zeitpunkt $t = 2.5 \text{ms}$.

Hinweise:

• Die Aufgabe gehört zum Kapitel Faltungssatz und Faltungsoperation.
• Sie bezieht sich vorwiegend auf die Seite Grafische Faltung
• Die Thematik dieses Abschnitts wird auch im Interaktionsmodul Zur Verdeutlichung der grafischen Faltung veranschaulicht.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Berechnen Sie die Signalwerte zu den Zeitpunkten $t = 1 \,\text{ms}$ und $t = 2 \,\text{ms}$.

$y(t = 1 \,\text{ms})$  =  $\text{V}$

$y(t = 2 \,\text{ms})$  =  $\text{V}$

2

Bestimmen Sie die Signalwerte für die Zeitpunkte $t = 3 \,\text{ms}$ und $t = 4 \,\text{ms}$ durch Ausnutzung der angegebenen Symmetrieeigenschaften.

$y(t = 3 \,\text{ms})$  =  $\text{V}$

$y(t = 4 \,\text{ms})$  =  $\text{V}$

3

Welche der folgenden Aussagen sind zutreffend?

	Das Ausgangssignal ${y(t)}$ hat einen trapezförmigen Verlauf.
	Das Spektrum lautet: ${Y(f)} = Y_0 \cdot \text{si}^{2}(\pi f T)$.
	Mit $T = 2 \,\text{ms}$ würde sich eine Dreiecksform ergeben.

Musterlösung

Solution

1. Allgemein gilt für das Faltungsintegral:

$$y(t) = \int_{ - \infty }^{ + \infty } {x( \tau ) \cdot h( {t - \tau } )}\hspace{0.1cm} {\rm d}\tau.$$

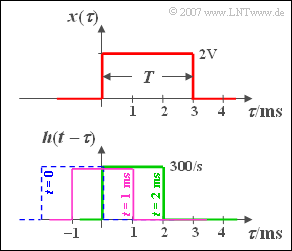
Hinweis: Die Abszissen in nebenstehender Grafik wurden zu $\tau$ umbenannt.

Der Signalwert zum Zeitpunkt $t = 1 \,\text{ms}$ kann wie folgt berechnet werden:

• Spiegelung der Impulsantwort ${h(\tau)}$,
• Verschiebung um $t = 1 \text{ms}$ nach rechts (violette Kurve in der Skizze),
• Multiplikation der beiden Funktionen sowie Integration.

Das Produkt ist ebenfalls rechteckförmig mit der Höhe $2 \text{V} \cdot 300 \; \text{1/s}$ und der Breite $1 \,\text{ms}$. Daraus ergibt sich für die Fläche:

$$y( {t = 1\;{\rm{ms}}} ) \hspace{0.15 cm}\underline{= 0.6\;{\rm{V}}}{\rm{.}}$$

Das grüne Rechteck verdeutlicht die Berechnung des zweiten Signalwertes. Nun ist das resultierende Rechteck nach der Multiplikation doppelt so breit und man erhält:

$$y( {t = 2\;{\rm{ms}}} ) = 2\;{\rm{V}} \cdot {\rm{300}}\;{1}/{{\rm{s}}} \cdot 2\;{\rm{ms}}\hspace{0.15 cm}\underline{={\rm{1.2}}\;{\rm{V}}}{\rm{.}}$$

2. Wegen der Symmetrie von ${y(t)}$ bezüglich des Zeitpunktes $t = 2.5\, \text {ms}$ gilt:

$$y( {t = 3\;{\rm{ms}}} ) = y( {t = 2\;{\rm{ms}}} ) \hspace{0.15 cm}\underline{= {\rm{1}}{\rm{.2}}\;{\rm{V}}}{\rm{,}}$$

$$y( {t = 4\;{\rm{ms}}} ) = y( {t = 1\;{\rm{ms}}} )\hspace{0.15 cm}\underline{ = 0.6\;{\rm{V}}}{\rm{.}}$$

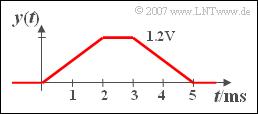
3. In den Teilaufgaben (1) und (2) wurden die Signalwerte zu diskreten Zeitpunkten berechnet. Alle Punkte sind durch Geradenstücke zu verbinden, da die Integration über Rechteckfunktionen wachsender Breite einen linearen Verlauf ergibt. Das heißt: ${y(t)}$ ist trapezförmig.

Das dazugehörige Spektrum ist komplex und lautet:

$$Y(f) = 6 \cdot 10^{ - 3} \;{{\rm{V}}}/{{{\rm{Hz}}}} \cdot {\mathop{\rm si}\nolimits} ( {2\;{\rm{ms}}\cdot{\rm{\pi }}f} ) \cdot {\mathop{\rm si}\nolimits} ( {3\;{\rm{ms}}\cdot{\rm{\pi }}f}) \cdot {\rm{e}}^{ - {\rm{j \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \hspace{0.05cm}\cdot \hspace{0.05cm}2.5\;{\rm{ms}}\hspace{0.05cm}\cdot \hspace{0.05cm} \pi }}f} .$$

• Hätte der Eingangsimpuls ${x(t)}$ die Dauer $T = 2\, \text {ms}$, so würde ${y(t)}$ einen dreieckförmigen Signalverlauf zwischen ${t = 0}$ und $t = 4 \, \text {ms}$ zeigen.
• Das Maximum $1.2 \, \text {V}$ ergäbe sich dann nur zum Zeitpunkt $t = 2 \, \text {ms}$.

Richtig sind somit die Lösungsvorschläge 1 und 3.