Aufgaben:Exercise 3.5: Triangular and Trapezoidal Signal

• Return to book

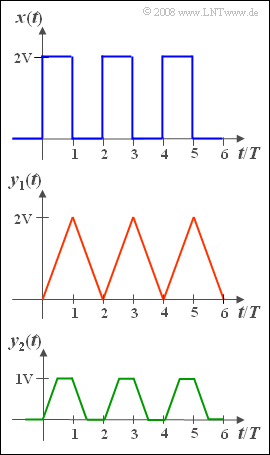
Wir gehen vom Rechtecksignal $x(t)$ gemäß der oberen Grafik aus.

• Die Amplitudenwerte sind $0\hspace{0.05cm} \rm V$ und $2\hspace{0.05cm} \rm V$.
• Die Dauer eines Rechtecks sowie der Abstand zweier aufeinander folgender Rechteckimpulse seien jeweils gleich $T$.
• Die Zufallsgröße $x$ – der Momentanwert des Rechtecksignals $x(t)$ – hat somit folgende Kennwerte:

$$m_x = \sigma_x = 1\hspace{0.05cm} \rm V.$$

Gibt man nun dieses Signal auf ein lineares Filter mit der Impulsantwort $$h_{\rm 1}(t)=\left \{ \begin{array}{*{4}{c}} 1/T & {\; \rm f\ddot{u}r}\hspace{0.1cm}{ 0\le t \le T} \\\ 0 & {\rm sonst} \end{array} \right. , $$

so ergibt sich an dessem Ausgang entsprechend der Faltung das Dreiecksignal $y_1(t) = x(t) \star h_1(t)$ mit

• den Minimalwerten $0\hspace{0.05cm} \rm V$ (bei $t = 0, 2T, 4T,$ ...),
• den Maximalwerten $2\hspace{0.05cm} \rm V$ (bei $t = T, 3T, 5T,$ ...).

Bei diesem Tiefpassfilter handelt es sich also um einen Integrator über die Zeitdauer $T$.

Legt man dagegen das Rechtecksignal$x(t)$ an den Eingang eines Filters mit der Impulsantwort $$h_{\rm 2}(t)=\left \{ \begin{array}{*{4}{c}} 1/T & {\; \rm f\ddot{u}r}\hspace{0.1cm}{ 0\le t \le T/2} \\\ 0 & {\rm sonst} \end{array} \right. , $$

so ergibt sich das trapezförmige Signal $y_2(t) = x(t) \star h_2(t)$. Dieses zweite Filter wirkt somit als ein Integrator über die Zeitdauer $T/2$.

Hinweise:

• Die Aufgabe gehört zum Kapitel Gleichverteilte Zufallsgröße.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Für die zugehörigen Frequenzgänge gilt $H_1(f=0)= 1$ bzw. $H_2(f=0)= 0.5$.

Fragebogen

1

Welche der folgenden Aussagen sind zutreffend?

	$y_1(t)$ ist eine kontinuierliche Zufallsgröße.
	$y_1(t)$ besitzt eine dreieckförmige WDF.
	$y_1(t)$ ist gleichverteilt.
	$y_2(t)$ hat kontinuierliche und diskrete Anteile.

2

Wie groß ist der Gleichanteil des Signals $y_1(t)$? Überprüfen Sie diesen Wert auch anhand der Größen $m_x$ und $H_1(f=0)$.

$m_{y1} \ =$ $\ \rm V$

3

Bestimmen Sie die Leistung des Signals $y_1(t)$ sowohl durch Zeitmittelung als auch durch Scharmittelung.

$P_{y1} \ =$ $\ \rm V^2$

4

Wie groß ist der Effektivwert des Signals $y_1(t)$?

$\sigma_{y1} \ =$ $\ \rm V$

5

Wie groß ist die Wahrscheinlichkeit, dass $y_1(t)$ größer ist als $0.75\hspace{0.05cm} \rm V$?

${\rm Pr}(y_1 > 0.75\hspace{0.05cm} \rm V) \ =$

6

Ermitteln Sie die WDF des Signals $y_2(t)$ und skizzieren Sie diese. Geben Sie zur Kontrolle den WDF-Wert an der Stelle $y_2 = 0.5\hspace{0.05cm} \rm V$ ein.

$f_{y2}(y_2= 0.5\hspace{0.05cm} \rm V) \ =$ $\ \rm 1/V$

7

Wie groß ist der Gleichanteil des Signals $y_2(t)$? Überprüfen Sie diesen Wert auch anhand der Größen $m_x$ und $H_2(f=0)$.

$m_{y2} \ =$ $\ \rm V$

8

Wie groß ist der Effektivwert des Signals $y_2(t)$?

$\sigma_{y2} \ =$ $\ \rm V$

9

Wie groß ist die Wahrscheinlichkeit, dass $y_2(t)$ größer ist als $0.75\hspace{0.05cm} \rm V$?

${\rm Pr}(y_2 > 0.75\hspace{0.05cm} \rm V) \ =$

Musterlösung

Solution

(1)  Richtig sind die Lösungsvorschläge 1, 3 und 4:

• Die Zufallsgröße $y_1$ ist gleichverteilt und dadurch natürlich auch eine kontinuierliche Zufallsgröße.
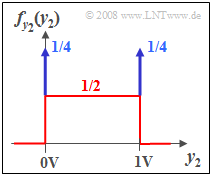
• Die WDF von $y_2$ weist diskrete Anteile bei $0\hspace{0.05cm} \rm V$ und $2\hspace{0.05cm} \rm V$ auf.
• Zwischen diesen zwei Begrenzungen gibt es selbstverständlich auch kontinuierliche Anteile. In diesem Bereich gilt $f_x(x) = 1/2$.

(2)  Der lineare Mittelwert $m_x = 1\hspace{0.05cm} \rm V$ ist aus der Angabenskizze direkt abzulesen, könnte aber auch formal mit der Gleichung für die Gleichverteilung (zwischen $0\hspace{0.05cm} \rm V$ und $2\hspace{0.05cm} \rm V$) berechnet werden. Eine weitere Lösungsmöglichkeit bietet die Beziehung: $$m_{y_{\rm 1}}=m_x\cdot H_{\rm 1}( f= 0) = 1\hspace{0.05cm} \rm V \cdot 1 \hspace{0.15cm}\underline{ =\rm 1\hspace{0.05cm} \rm V}.$$

(3)  Eigentlich müsste die Mittelung über den gesamten Zeitbereich (beidseitig bis ins Unendliche) erfolgen. Aus Symmetriegründen genügt jedoch die Mittelung über das Zeitintervall $0 \le t \le T$: $$P_{y_{\rm 1}}=\rm\frac{1}{\it T}\cdot \int_{\rm 0}^{\it T} \hspace{-0.15cm}\it y_{\rm 1}(\it t{\rm )}^{\rm 2}\it \hspace{0.05cm}\hspace{0.1cm}{\rm d}t=\rm\frac{1}{\it T}\cdot \int_{\rm 0}^{\it T} \hspace{-0.15cm}(\rm 2V \cdot \it\frac{t}{T})^{\rm 2} \hspace{0.1cm}{\rm d} t = \rm {4}/{3}\, V^2 \hspace{0.15cm}\underline{= \rm 1.333\, V^2}.$$

Die Scharmittelung liefert das gleiche Ergebnis. Mit der WDF $f_{y1}(y_1) = 1/(2\hspace{0.05cm} \rm V)$ gilt nämlich: $$P_{y_{\rm 1}}= \int_0^{2V} \hspace{-0.3cm}\it y_{\rm 1}^{\rm 2}\cdot f_{\it y_{\rm 1}}(\it y_{\rm 1})\it \hspace{0.1cm}{\rm d}y_{\rm 1} =\rm\frac{1}{2V}\cdot \int_0^{2V} \hspace{-0.3cm}\it y_{\rm 1}^{\rm 2}\hspace{0.1cm}{\rm d}y_{\rm 1} =\rm \frac{8\,{\rm V^3}}{3 \cdot 2\,{\rm V}} \hspace{0.15cm}\underline{= \rm 1.333\, V^2}.$$

(4)  Die Varianz kann mit dem Satz von Steiner ermittelt werden und ergibt $4/3\hspace{0.05cm} \rm V^2 - 1\hspace{0.05cm} \rm V^2 = 1/3\hspace{0.05cm} \rm V^2$. Die Wurzel daraus ist die gesuchte Streuung (der Effektivwert): $\sigma_{y_{\rm 1}}\hspace{0.15cm}\underline{=0.577 \, \rm V}.$

(5)  Die gesuchte Wahrscheinlichkeit ist das Integral über die WDF von $0.75\hspace{0.05cm} \rm V$ bis $2\hspace{0.05cm} \rm V$, also ${\rm Pr}(y_1 > 0.75\hspace{0.05cm} \rm V) \hspace{0.15cm}\underline{ =0.625}$.

(6)  Die WDF besteht aus zwei Diracfunktionen bei $0\hspace{0.05cm} \rm V$ und $1\hspace{0.05cm} \rm V$ (jeweils mit dem Gewicht $1/4$) und einem konstanten kontinuierlichen Anteil von $f_{y2}(y_2= 0.5\hspace{0.05cm} \rm V) \hspace{0.15cm}\underline{=0.5 \cdot\rm 1/V}$ . Bei $y_2 = 0.5 \hspace{0.05cm} \rm V$ gibt es deshalb nur den kontinuierlichen Anteil.

(7)  Der Mittelwert $m_{y_{\rm 2}}=m_x\cdot H_{\rm 1}( f= 0) { =\rm 0.5\hspace{0.05cm} \rm V}$ kann direkt aus obiger WDF-Skizze abgelesen werden oder wie in derr Teilaufgabe (2) über die Beziehung $m_{y_{\rm 2}}=m_x\cdot H_{\rm 2}( f= 0) = 1\hspace{0.05cm} \rm V \cdot 0.5 { =\rm 0.5\hspace{0.05cm} \rm V}$ berechnet werden.

(8)  Mit obiger WDF gilt für die Leistung: $$P_{y_{\rm 2}}=\int_{-\infty}^{+\infty}\hspace{-0.3cm}y_{\rm 2}^{\rm 2}\cdot f_{\it y_{\rm 2}}(\it y_{\rm 2})\hspace{0.1cm}{\rm d}y_{\rm 2}=\rm \frac{1}{2}\cdot\frac{1}{3}\cdot 1\,V^2+\rm \frac{1}{4}\cdot 1\,V^2 = 5/12 \,V^2 \hspace{0.15cm}{ =\rm 0.417\,V^2}.$$

Der erste Anteil geht auf die kontinuierliche WDF zurück, der zweite auf die WDF–Diracfunktion bei $1\hspace{0.05cm} \rm V$. Die Diracfunktion bei $0\hspace{0.05cm} \rm V$ liefert keinen Beitrag zur Leistung. Daraus folgt für den Effektivwert: $$\sigma_{y_{\rm 2}} = \sqrt{{\rm 5}/{\rm 12}\rm V^2 -{1}/{4}\rm V^2}= \sqrt{{\rm 1}/{\rm 6}\rm V^2} \hspace{0.15cm}\underline{=0.409\, \rm V}.$$

(9)  Diese Wahrscheinlichkeit setzt sich ebenfalls aus zwei Anteilen zusammen: $${\rm Pr}(y_2 > 0.75 {\rm V} ) = {\rm Pr}(0.75 {\rm V} \le y_2 < 1 {\rm V} ) + {\rm Pr}(y_2 = 1 {\rm V} ) = \frac{1}{2} \cdot \frac{1}{4}+ \frac{1}{4} = \frac{3}{8}\hspace{0.15cm}\underline{ = 0.375}. $$