Difference between revisions of "Applets:Linear Distortions of Periodic Signals"
| Line 34: | Line 34: | ||
*the Distortion Power $P_{\rm D}$ and | *the Distortion Power $P_{\rm D}$ and | ||
*the Signal–to–Distortion Ratio (abbr.: SDR) | *the Signal–to–Distortion Ratio (abbr.: SDR) | ||
| − | :$$\rho_{\rm D}=\frac{\rm Signal | + | :$$\rho_{\rm D}=\frac{\rm Signal Power}{\rm Distortion Power} = \frac{P_x}{P_{\rm D} }.$$ |
| Line 44: | Line 44: | ||
[[File:LZI_T_2_2_S3_vers2.png|center|frame|For clarification of nonlinear distortions |class=fit]] | [[File:LZI_T_2_2_S3_vers2.png|center|frame|For clarification of nonlinear distortions |class=fit]] | ||
| − | [[File:P_ID899__LZI_T_2_3_S1_neu.png|right |frame| | + | [[File:P_ID899__LZI_T_2_3_S1_neu.png|right |frame| Description of a linear system|class=fit]] |
| − | *''' | + | *'''Linear distortions'''occur, if the transmission channel is characterized by a frequency response $H(f) \ne \rm const.$. Various frequencies are attenuated and delayed differently. Characteristic of this is that although frequencies can disappear (for example, through a low pass or a high pass), no new frequencies can arise. |
| − | In | + | In this applet only linear distortions are considered. |
| − | === | + | === Description forms for the frequency response === |
<br> | <br> | ||
| − | + | The generally complex valued frequency response can be represented as follows: | |
:$$H(f) = |H(f)| \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot | :$$H(f) = |H(f)| \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot | ||
\hspace{0.05cm} b(f)} = {\rm e}^{-a(f)}\cdot {\rm e}^{-{\rm j} | \hspace{0.05cm} b(f)} = {\rm e}^{-a(f)}\cdot {\rm e}^{-{\rm j} | ||
\hspace{0.05cm} \cdot \hspace{0.05cm} b(f)}.$$ | \hspace{0.05cm} \cdot \hspace{0.05cm} b(f)}.$$ | ||
| − | + | This results in the following description variables: | |
| − | * | + | *The absolute value $|H(f)|$ is called '''Amplitude response''' and in logarithmic form '''Attenuation curve''' bezeichnet: |
:$$a(f) = - \ln |H(f)|\hspace{0.2cm}{\rm in \hspace{0.1cm}Neper | :$$a(f) = - \ln |H(f)|\hspace{0.2cm}{\rm in \hspace{0.1cm}Neper | ||
\hspace{0.1cm}(Np) } = - 20 \cdot \lg |H(f)|\hspace{0.2cm}{\rm in | \hspace{0.1cm}(Np) } = - 20 \cdot \lg |H(f)|\hspace{0.2cm}{\rm in | ||
| − | \hspace{0.1cm} | + | \hspace{0.1cm}Decibel \hspace{0.1cm}(dB) }.$$ |
| − | * | + | *The '''Phase response''' $b(f)$ indicates the negative frequency–dependent angle of $H(f)$ in the complex plane based on the real axis: |
:$$b(f) = - {\rm arc} \hspace{0.1cm}H(f) \hspace{0.2cm}{\rm in | :$$b(f) = - {\rm arc} \hspace{0.1cm}H(f) \hspace{0.2cm}{\rm in | ||
\hspace{0.1cm}Radian \hspace{0.1cm}(rad)}.$$ | \hspace{0.1cm}Radian \hspace{0.1cm}(rad)}.$$ | ||
| − | === | + | === <i>N^{th}</i> grade low pass === |
<br> | <br> | ||
| − | + | The frequency response of a realizable <i>N^{th}</i> grade low pass is: | |
:$$H(f) = \left [\frac{1}{1 + {\rm j}\cdot f/f_0 }\right ]^N\hspace{0.05cm}.$$ | :$$H(f) = \left [\frac{1}{1 + {\rm j}\cdot f/f_0 }\right ]^N\hspace{0.05cm}.$$ | ||
| − | + | An example is the RC–low pass with $N = 1$. Consequently we can obtain | |
| − | * | + | *the attenuation curve: |
:$$a(f) =N/2 \cdot \ln [1+( f/f_0)^2] \hspace{0.05cm},$$ | :$$a(f) =N/2 \cdot \ln [1+( f/f_0)^2] \hspace{0.05cm},$$ | ||
| − | * | + | *the phase curve: |
:$$b(f) =N \cdot \arctan( f/f_0) \hspace{0.05cm},$$ | :$$b(f) =N \cdot \arctan( f/f_0) \hspace{0.05cm},$$ | ||
| − | * | + | *the attenuation factor for the frequency $f=f_i$: |
:$$\alpha_i =|H(f = f_i)| = [1+( f/f_0)^2]^{N/2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x(t)= A_i\cdot \cos(2\pi f_i t) \hspace{0.1cm}\rightarrow \hspace{0.1cm} y(t)= \alpha_i \cdot A_i\cdot \cos(2\pi f_i t)\hspace{0.05cm},$$ | :$$\alpha_i =|H(f = f_i)| = [1+( f/f_0)^2]^{N/2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x(t)= A_i\cdot \cos(2\pi f_i t) \hspace{0.1cm}\rightarrow \hspace{0.1cm} y(t)= \alpha_i \cdot A_i\cdot \cos(2\pi f_i t)\hspace{0.05cm},$$ | ||
| − | * | + | *the phase delay for the frequency $f=f_i$: |
:$$\tau_i =\frac{b(f_i)}{2 \pi f_i} = \frac{N \cdot \arctan( f_i/f_0)}{2 \pi f_i} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x(t)= A_i\cdot \cos(2\pi f_i t) \hspace{0.1cm}\rightarrow \hspace{0.1cm} y(t)=A_i\cdot \cos(2\pi f_i (t- \tau_i))\hspace{0.05cm},$$ | :$$\tau_i =\frac{b(f_i)}{2 \pi f_i} = \frac{N \cdot \arctan( f_i/f_0)}{2 \pi f_i} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x(t)= A_i\cdot \cos(2\pi f_i t) \hspace{0.1cm}\rightarrow \hspace{0.1cm} y(t)=A_i\cdot \cos(2\pi f_i (t- \tau_i))\hspace{0.05cm},$$ | ||
| − | [[File:Tiefpass.png|center|frame| | + | [[File:Tiefpass.png|center|frame|Attenuation and phase curve of an <i>N^{th}</i> grade low pass]] |
=== Hochpass <i>N</i>–Ordnung === | === Hochpass <i>N</i>–Ordnung === | ||
Revision as of 22:36, 14 January 2018
Contents
Applet description
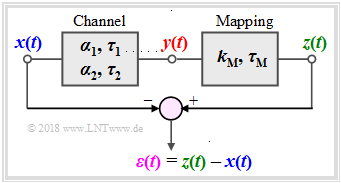
This applet showcases the effects of linear distortions(attenuation distortions and phase distortions) with
- the input signal $x(t)$ ⇒ Power $P_x$:
- $$x(t) = x_1(t) + x_2(t) = A_1\cdot \cos\left(2\pi f_1\cdot t- \varphi_1\right)+A_2\cdot \cos\left(2\pi f_2\cdot t- \varphi_2\right), $$
- the output signal $y(t)$ ⇒ output signal $P_y$:
- $$y(t) = \alpha_1 \cdot x_1(t-\tau_1) + \alpha_2 \cdot x_2(t-\tau_2),$$
- the matching output signal $z(t)$ ⇒ Power $P_z$:
- $$z(t) = k_{\rm M} \cdot y(t-\tau_{\rm M}) + \alpha_2 \cdot x_2(t-\tau_2),$$
- the differential signal $\varepsilon(t) = z(t) - x(t)$ ⇒ Power $P_\varepsilon$.
The adjustment of the output signal's amplitude and phase $y(t)$ ⇒ „Matching” allows for a differentiation between
- attenuation distortion and frequency–independant attenuation, as well as
- phase distortion and pure running time.
The Distortion Power $P_{\rm D}$ is used to measure the strength of the linear distortion.
Theoretical background
Distortions refer to generally unwanted alterations of a message signal through a transmission system. Together with the strong stochastic effects (noise, crosstalk, etc.), they are a crucial limitation for the quality and rate of transmission.
Just as the „Stärke” of noise can be assessed through
- the Noise Power $P_{\rm N}$ and
- the Signal–to–Noise Ratio (abbr.: SNR) $\rho_{\rm N}$,
distortions can be quantified through
- the Distortion Power $P_{\rm D}$ and
- the Signal–to–Distortion Ratio (abbr.: SDR)
- $$\rho_{\rm D}=\frac{\rm Signal Power}{\rm Distortion Power} = \frac{P_x}{P_{\rm D} }.$$
Linear and nonlinear distortions
A distinction is made between linear and nonlinear distortions:
- Nonlinear distortions occur, if at all times $t$ the nonlinear correlation $y = g(x) \ne {\rm const.} \cdot x$ exists between the signal values $x = x(t)$ at the input and $y = y(t)$ at the output, whereby $y = g(x)$ is defined as the system's nonlinear characteristic. By creating a cosine signal at the input with frequency $f_0$ the output signal value includes $f_0$ as well as multiple harmonic waves. We conclude that new frequencies arise through nonlinear distortion.
- Linear distortionsoccur, if the transmission channel is characterized by a frequency response $H(f) \ne \rm const.$. Various frequencies are attenuated and delayed differently. Characteristic of this is that although frequencies can disappear (for example, through a low pass or a high pass), no new frequencies can arise.
In this applet only linear distortions are considered.
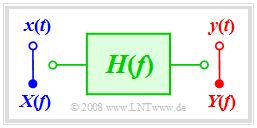
Description forms for the frequency response
The generally complex valued frequency response can be represented as follows:
- $$H(f) = |H(f)| \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b(f)} = {\rm e}^{-a(f)}\cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b(f)}.$$
This results in the following description variables:
- The absolute value $|H(f)|$ is called Amplitude response and in logarithmic form Attenuation curve bezeichnet:
- $$a(f) = - \ln |H(f)|\hspace{0.2cm}{\rm in \hspace{0.1cm}Neper \hspace{0.1cm}(Np) } = - 20 \cdot \lg |H(f)|\hspace{0.2cm}{\rm in \hspace{0.1cm}Decibel \hspace{0.1cm}(dB) }.$$
- The Phase response $b(f)$ indicates the negative frequency–dependent angle of $H(f)$ in the complex plane based on the real axis:
- $$b(f) = - {\rm arc} \hspace{0.1cm}H(f) \hspace{0.2cm}{\rm in \hspace{0.1cm}Radian \hspace{0.1cm}(rad)}.$$
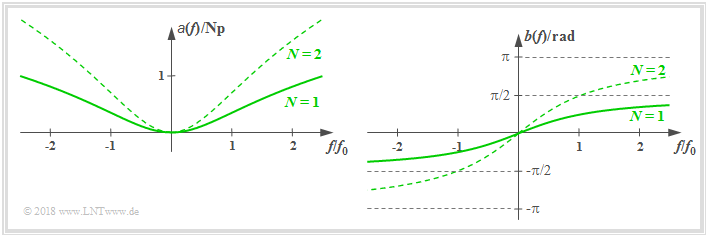
N^{th} grade low pass
The frequency response of a realizable N^{th} grade low pass is:
- $$H(f) = \left [\frac{1}{1 + {\rm j}\cdot f/f_0 }\right ]^N\hspace{0.05cm}.$$
An example is the RC–low pass with $N = 1$. Consequently we can obtain
- the attenuation curve:
- $$a(f) =N/2 \cdot \ln [1+( f/f_0)^2] \hspace{0.05cm},$$
- the phase curve:
- $$b(f) =N \cdot \arctan( f/f_0) \hspace{0.05cm},$$
- the attenuation factor for the frequency $f=f_i$:
- $$\alpha_i =|H(f = f_i)| = [1+( f/f_0)^2]^{N/2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x(t)= A_i\cdot \cos(2\pi f_i t) \hspace{0.1cm}\rightarrow \hspace{0.1cm} y(t)= \alpha_i \cdot A_i\cdot \cos(2\pi f_i t)\hspace{0.05cm},$$
- the phase delay for the frequency $f=f_i$:
- $$\tau_i =\frac{b(f_i)}{2 \pi f_i} = \frac{N \cdot \arctan( f_i/f_0)}{2 \pi f_i} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x(t)= A_i\cdot \cos(2\pi f_i t) \hspace{0.1cm}\rightarrow \hspace{0.1cm} y(t)=A_i\cdot \cos(2\pi f_i (t- \tau_i))\hspace{0.05cm},$$
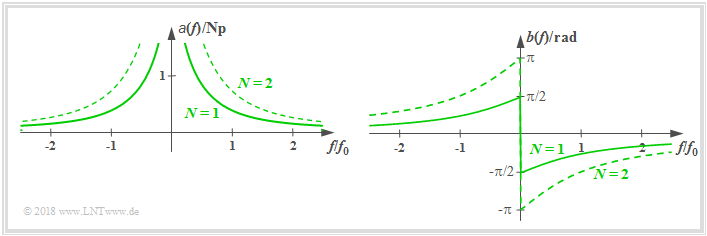
Hochpass N–Ordnung
Der Frequenzgang eines realisierbaren Hochpasses N–Ordnung lautet:
- $$H(f) = \left [\frac{ {\rm j}\cdot f/f_0 }{1 + {\rm j}\cdot f/f_0 }\right ]^N\hspace{0.05cm}.$$
Ein einfacher LC–Tiefpass hat diesen Verlauf mit $N=1$. Damit erhält man
- den Dämpfungsverlauf:
- $$a(f) =N/2 \cdot \ln [1+( f_0/f)^2] \hspace{0.05cm},$$
- den Phasenverlauf:
- $$b(f) =-N \cdot \arctan( f_0/f) \hspace{0.05cm},$$
- den Dämpfungsfaktor für die Frequenz $f=f_i$:
- $$\alpha_i =|H(f = f_i)| = [1+( f_0/f)^2]^{N/2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x(t)= A_i\cdot \cos(2\pi f_i t) \hspace{0.1cm}\rightarrow \hspace{0.1cm} y(t)= \alpha_i \cdot A_i\cdot \cos(2\pi f_i t)\hspace{0.05cm},$$
- die Phasenlaufzeit für die Frequenz $f=f_i$:
- $$\tau_i =\frac{b(f_i)}{2\pif_i} = \frac{-N \cdot \arctan( f_0/f_i)}{2\pif_i} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x(t)= A_i\cdot \cos(2\pi f_i t) \hspace{0.1cm}\rightarrow \hspace{0.1cm} y(t)=A_i\cdot \cos(2\pi f_i (t- \tau_i))\hspace{0.05cm},$$
Laufzeiten bei Tiefpass und Hochpass
Mache ich noch
Dämpfungsverzerrungen und Phasenverzerrungen
Überarbeite ich noch
Lineare Verzerrungen treten üblicherweise in Form von
- Dämpfungsverzerrungen $\alpha_i$ und
- Phasenverzerrungen $\tau_i$ auf.
Ist $\alpha_1 \ne \alpha_2$ und $\tau_1 = \tau_2$, so liegen ausschließlich Dämpfungsverzerrungen vor.
Dagegen führt $\alpha_1 = \alpha_2$ und $\tau_1 \ne \tau_2$ zu reinen Phasenverzerrungen.
Ein Signal $y(t)$ ist gegenüber $x(t)$ unverzerrt, wenn $\alpha_1 = \alpha_2$ und $\tau_1 und \tau_2$ gilt.
Vorschlag für die Versuchsdurchführung
BlaBla
(1) Für das Sendesignal $x(t)$ gelte $A_1 = 0.8\ {\rm V}, \ A_2 = 0.6\ {\rm V}, \ f_1 = 0.5\ {\rm kHz}, \ f_2 = 1.5\ {\rm kHz}, \ \varphi_1 = 90^\circ, \ \varphi_2 = 0^\circ$.
- Wie groß ist die Periodendauer $T_0$? Welche Leistung $P_x$ weist dieses Signal auf? Wo können Sie diesen Wert im Programm ablesen?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}T_0 = \big [\hspace{-0.1cm}\text{ größter gemeinsamer Teiler }(0.5 \ {\rm kHz}, \ 1.5 \ {\rm kHz})\big ]^{-1}\hspace{0.15cm}\underline{ = 2.0 \ {\rm ms}};$
$\hspace{1.85cm} P_x = A_1^2/2 + A_2^2/2 \hspace{0.15cm}\underline{= 0.5 \ {\rm V^2}} = P_\varepsilon\text{, wenn }\hspace{0.15cm}\underline{k_{\rm M} = 0} \ \Rightarrow \ z(t) \equiv 0$.
(2) Variieren Sie bei sonst gleicher Einstellung wie unter (1) die Phase $\varphi_2$ im gesamten möglichen Bereich $\pm 180^\circ$. Wie ändern sich $T_0$ und $P_x$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Keine Veränderungen:}\hspace{0.2cm}\hspace{0.15cm}\underline{ T_0 = 2.0 \ {\rm ms}; \hspace{0.2cm} P_x = 0.5 \ {\rm V^2}}$.
(3) Variieren Sie bei sonst gleicher Einstellung wie unter (1) die Frequenz $f_2$ im Bereich $0 \le f_2 \le 5\ {\rm kHz}$. Wie ändert sich die Signalleistung $P_x$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Keine Veränderungen, falls }f_2 \ne 0\text{ oder } f_2 \ne f_1\text{:}\hspace{0.3cm} \hspace{0.15cm}\underline{P_x = 0.5 \ {\rm V^2}}\text{.} \hspace{0.2cm} T_0 \text{ ändert sich, falls }f_2\text{ kein Vielfaches von }f_1$.
$\hspace{1.85cm}\text{Falls }f_2 = 0\text{:}\hspace{0.2cm} P_x = A_1^2/2 + A_2^2\hspace{0.15cm}\underline{ = 0.68 \ {\rm V^2}}$. $\hspace{3cm}\text{Allgemeine Formel noch überprüfen}$
$\hspace{1.85cm}\text{Falls }f_2 = f_1\text{:}\hspace{0.2cm} P_x = [A_1\cos(\varphi_1) + A_2\cos(\varphi_2)]^2/2 + [A_1\sin(\varphi_1) + A_2\sin(\varphi_2)]^2/2 \text{. Mit } \varphi_1 = 90^\circ, \ \varphi_2 = 0^\circ\text{:}\hspace{0.3cm}\hspace{0.15cm}\underline{ P_x = 0.5 \ {\rm V^2}}\text{.} $
(4) Ausgehend vom bisherigen Sendesignal $x(t)$ gelte für den Kanal: $\alpha_1 = \alpha_2 = 0.5, \ \tau_1 = \tau_2 = 0.5\ {\rm ms}$. Zudem sei $k_{\rm M} = 1 \text{ und } \tau_{\rm M} = 0$ .
- Gibt es lineare Verzerrungen? Wie groß ist die Empfangsleistung $P_y$ und die Leistung $P_\varepsilon$ des Differenzsignals $\varepsilon(t) = z(t) - x(t)$?
$\hspace{1.0cm}\Rightarrow \hspace{0.3cm}\hspace{0.15cm}\underline{ y(t) = 0.5 \cdot x(t- 1\ {\rm ms})}\text{ ist unverzerrt, nur gedämpft und verzögert.}$
$\hspace{1.85cm}\text{Empfangsleistung:}\hspace{0.2cm} P_y = (A_1/2)^2/2 + (A_2/2)^2/2\hspace{0.15cm}\underline{ = 0.125 \ {\rm V^2}}\text{. } P_\varepsilon \text{ ist deutlich größer:} \hspace{0.1cm} \hspace{0.15cm}\underline{P_\varepsilon = 0.625 \ {\rm V^2}}.$
(5) Variieren Sie bei sonst gleicher Einstellung wie unter (4) die Matchingparameter $k_{\rm M} \text{ und } \tau_{\rm M}$. Wie groß ist die Verzerrungsleistung $P_{\rm D}$?
$\hspace{1.0cm}\Rightarrow \hspace{0.3cm} P_{\rm D}\text{ ist gleich der Leistung }P_\varepsilon \text{ des Differenzsignals bei bestmöglicher Anpassung:} \hspace{0.2cm}k_{\rm M} = 2 \text{ und } \tau_{\rm M}=T_0 - 0.5\ {\rm ms} = 1.5\ {\rm ms}$
$\hspace{1.0cm}\Rightarrow \hspace{0.3cm}z(t) = x(t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\varepsilon(t) = 0\hspace{0.3cm}\Rightarrow \hspace{0.3cm}P_{\rm D}\hspace{0.15cm}\underline{ = P_\varepsilon = 0} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\text{weder Dämpfungs- noch Phasenverzerrungen.}$
(6) Für den Kanal gelte nun $\alpha_1 = 0.5, \hspace{0.15cm}\underline{\alpha_2 = 0.2}, \ \tau_1 = \tau_2 = 0.5\ {\rm ms}$. Wie groß sind nun die Verzerrungsleistung $P_{\rm D}$ und das $\rm SDR$ $\rho_{\rm D}$?
$\hspace{1.0cm}\Rightarrow \hspace{0.3cm} P_{\rm D} = P_\varepsilon \text{ bei bestmöglicher Anpassung:} \hspace{0.2cm}\hspace{0.15cm}\underline{k_{\rm M} = 2.24} \text{ und } \hspace{0.15cm}\underline{\tau_{\rm M} = 1.5\ {\rm ms} }\text{:} \hspace{0.2cm}\hspace{0.15cm}\underline{P_{\rm D} = 0.059 \ {\rm V^2}}$.
$\hspace{1.85cm}\text{Nur Dämpfungsverzerrungen.} \hspace{0.3cm}\text{Signal-zu-Verzerrung-Leistungsverhältnis}\ \hspace{0.15cm}\underline{\rho_{\rm D} = P_x/P_\varepsilon \approx 8.5}$.
(7) Für den Kanal gelte nun $\alpha_1 = \alpha_2 = 0.5, \ \tau_1 \hspace{0.15cm}\underline{= 2\ {\rm ms} }, \ \tau_2 = 0.5\ {\rm ms}$. Wie groß sind nun $P_{\rm D}$ und $\rho_{\rm D}$?
$\hspace{1.0cm}\Rightarrow \hspace{0.3cm} P_{\rm D} = P_\varepsilon \text{ bei bestmöglicher Anpassung:} \hspace{0.2cm}\hspace{0.15cm}\underline{k_{\rm M} = 1.82} \text{ und } \tau_{\rm M}\hspace{0.15cm}\underline{ = 0.15\ {\rm ms} }\text{:} \hspace{0.2cm}\hspace{0.15cm}\underline{P_{\rm D} = 0.072 \ {\rm V^2}}$.
$\hspace{1.85cm}\text{Nur Phasenverzerrungen.} \hspace{0.3cm}\text{Signal-zu-Verzerrung-Leistungsverhältnis}\ \hspace{0.15cm}\underline{\rho_{\rm D} = P_x/P_\varepsilon \approx 7}$.
(8) Für den Kanal gelte nun $\hspace{0.15cm}\underline{\alpha_1 = 0.5} , \hspace{0.15cm}\underline{\alpha_2 = 0.2} , \ \hspace{0.15cm}\underline{\tau_1= 2\ {\rm ms} }, \ \hspace{0.15cm}\underline{\tau_2 = 0.5\ {\rm ms} }$. Wie groß sind nun $P_{\rm D}$ und $\rho_{\rm D}$? Wie lässt sich $y(t)$ annähern?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{Dämpfungs- und Phasenverzerrungen. Bestmögliche Anpassung:} \hspace{0.2cm}\hspace{0.15cm}\underline{k_{\rm M} = 2.06} \text{, } \hspace{0.15cm}\underline{\tau_{\rm M} = 0.15\ {\rm ms} }\text{:} \hspace{0.2cm}\hspace{0.15cm}\underline{P_{\rm D} = 0.136 \ {\rm V^2}},\hspace{0.1cm}\hspace{0.15cm}\underline{\rho_{\rm D} \approx 3.7}$.
$\hspace{1.85cm}\text{Zusammenfassen von }\varphi \text{- und } \tau\text{-Parameter: } y(t) = 0.4 \ {\rm V} \cdot \sin\ (2\pi f_1 t) - 0.12 \ {\rm V} \cdot \sin\ (2\pi \cdot 3f_1\cdot t) \hspace{0.15cm}\underline{\approx 0.52 \ {\rm V} \cdot \sin^3(2\pi f_1 t)}$.
(9) Nun gelte $\underline{A_1 = A_2 = 1\ {\rm V}, \ f_1 = 1\ {\rm kHz}, \ f_2 = 1\ {\rm kHz}, \ \varphi_1 = 0^\circ, \ \varphi_2 = 0^\circ}$. Der Kanal sei ein Tiefpass erster Ordnung $\underline{(f_0 = 1\ {\rm kHz})}$.
- Gibt es Dämpfungsverzerrungen? Gibt es Phasenverzerrungen? Wie groß ist nun die Verzerrungsleistung $P_{\rm D}$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{Dämpfungsverzerrungen, da }\hspace{0.15cm}\underline{\alpha_1 = 0.71 \ne \alpha_2 = 0.45} \text{; geringere Phasenverzerrungen, da }\hspace{0.15cm}\underline{ \tau_1 = 0.13 \ {\rm ms} \approx \tau_2 = 0.09 \ {\rm ms}}$.
$\hspace{1.85cm}\text{ Verzerrungsleistung }\hspace{0.15cm}\underline{P_{\rm D} = 0.074 \ {\rm V^2}} \text{ bei bestmöglicher Anpassung:} \hspace{0.2cm}k_{\rm M}\hspace{0.15cm}\underline{ = 1.6} \text{ und } \tau_{\rm M}\hspace{0.15cm}\underline{ = 0.9\ {\rm ms} }$.
(10) Wie ändern sich die Kanalparameter durch einen Tiefpass zweiter Ordnung gegenüber einem Tiefpass erster Ordnung $(f_0 = 1\ {\rm kHz})$.
- Wie groß ist nun die Verzerrungsleistung $P_{\rm D}$? Wie groß ist nun die Verzerrungsleistung $P_{\rm D}$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{Es gilt }\hspace{0.15cm}\underline{\alpha_1 = 0.71^2 \approx 0.5, \alpha_2 = 0.45^2 \approx 0.5, \tau_1 = 2 \cdot 0.13 \approx 0.25 \ {\rm ms} \tau_2 = 2 \cdot 0.09 \ {\rm ms} \approx 0.18 \ {\rm ms}} $.
$\hspace{1.85cm}P_{\rm D} = 0.228 \ {\rm V^2} \text { ist größer und der 2 kHz-Anteil wird im Vergleich zum 2 kHz-Anteil noch mehr unterdrückt}$.
(11) Welche Unterschiede ergeben sich bei einem Hochpass zweiter Ordnung gegenüber einem Tiefpass zweiter Ordnung $(f_0 = 1\ {\rm kHz})$.
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{???????????????}$
Zur Handhabung des Applets
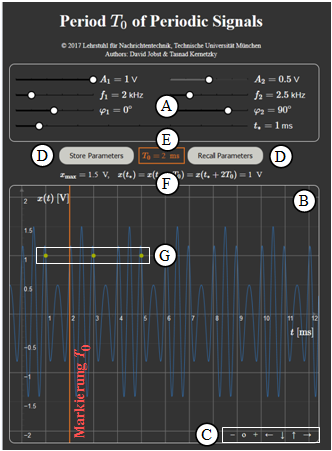
(A) Parametereingabe per Slider
(B) Bereich der graphischen Darstellung
(C) Variationsmöglichkeit für die graphische Darstellung
(D) Abspeichern und Zurückholen von Parametersätzen
(E) Numerikausgabe des Hauptergebnisses $T_0$; graphische Verdeutlichung durch rote Linie
(F) Ausgabe von $x_{\rm max}$ und der Signalwerte $x(t_*) = x(t_* + T_0)= x(t_* + 2T_0)$
(G) Darstellung der Signalwerte $x(t_*) = x(t_* + T_0)= x(t_* + 2T_0)$ durch grüne Punkte
(H) Einstellung der Zeit $t_*$ für die Signalwerte $x(t_*) = x(t_* + T_0)= x(t_* + 2T_0)$
Details zum obigen Punkt (C)
(*) Zoom–Funktionen „$+$” (Vergrößern), „$-$” (Verkleinern) und $\rm o$ (Zurücksetzen)
(*) Verschieben mit „$\leftarrow$” (Ausschnitt nach links, Ordinate nach rechts), „$\uparrow$” „$\downarrow$” und „$\rightarrow$”
Andere Möglichkeiten:
(*) Gedrückte Shifttaste und Scrollen: Zoomen im Koordinatensystem,
(*) Gedrückte Shifttaste und linke Maustaste: Verschieben des Koordinatensystems.
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2005 von Bettina Hirner im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder ).
- 2018 wurde dieses Programm von Jimmy He im Rahmen seiner Bachelorarbeit (Betreuer: Tasnád Kernetzky) auf „HTML5” umgesetzt und neu gestaltet.