Difference between revisions of "Aufgaben:Exercise 3.2Z: Sinc-Squared Spectrum with Diracs"
| Line 40: | Line 40: | ||
| − | {Wie groß ist die Amplitude $C$ des periodischen Anteils von x(t)? | + | {Wie groß ist die Amplitude $C$ des periodischen Anteils von $x(t)$? |
|type="{}"} | |type="{}"} | ||
$C\ = \ $ { 1 3% } $\text{V}$ | $C\ = \ $ { 1 3% } $\text{V}$ | ||
| − | {Wie groß sind der Maximalwert und der Minimalwert des Signals $ | + | {Wie groß sind der Maximalwert und der Minimalwert des Signals $x(t)$? |
|type="{}"} | |type="{}"} | ||
$x_\text{max}\ = \ $ { 2 3% } $\text{V}$ | $x_\text{max}\ = \ $ { 2 3% } $\text{V}$ | ||
| − | $x_\text{min}\ = \ $ { -2.06--1.94 } $\text{V}$ | + | $x_\text{min}\hspace{0.2cm} = \ $ { -2.06--1.94 } $\text{V}$ |
| Line 57: | Line 57: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
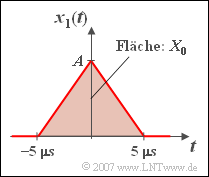
[[File:P_ID498__Sig_Z_3_2_a_neu.png|right|frame|Dreieckimpuls]] | [[File:P_ID498__Sig_Z_3_2_a_neu.png|right|frame|Dreieckimpuls]] | ||
| − | '''(1)''' Die einseitige Dauer des symmetrischen Dreieckimpulses beträgt $T = 1/f_0 = 5 \,{\rm \mu s}$. Der Spektralwert $X_0 = X_1(f = 0)$ gibt die Impulsfläche von $x_1(t)$ an. Diese ist gleich ${A} \cdot {T}$. Daraus folgt: | + | '''(1)''' Die einseitige Dauer des symmetrischen Dreieckimpulses beträgt $T = 1/f_0\hspace{0.15 cm}\underline{ = 5 \,{\rm \mu s}}$. |
| + | |||
| + | Der Spektralwert $X_0 = X_1(f = 0)$ gibt die Impulsfläche von $x_1(t)$ an. Diese ist gleich ${A} \cdot {T}$. Daraus folgt: | ||
:$$A = \frac{X_0 }{T} = \frac{ 10^{-5}\rm V/Hz }{5 \cdot 10^{-6}{\rm s}}\hspace{0.15 cm}\underline{= 2\;{\rm V}}.$$ | :$$A = \frac{X_0 }{T} = \frac{ 10^{-5}\rm V/Hz }{5 \cdot 10^{-6}{\rm s}}\hspace{0.15 cm}\underline{= 2\;{\rm V}}.$$ | ||
| − | '''(2)''' Der Gleichsignalanteil ist durch das Diracgewicht bei | + | '''(2)''' Der Gleichsignalanteil ist durch das Diracgewicht bei $f = 0$ gegeben. Man erhält ${B} \hspace{0.15 cm}\underline{= -1 \,\text{V}}$. |
'''(3)''' Die beiden Spektrallinien bei $\pm f_0$ ergeben zusammen ein Cosinussignal mit der Amplitude ${C} \hspace{0.15 cm}\underline{= 1 \text{V}}$. | '''(3)''' Die beiden Spektrallinien bei $\pm f_0$ ergeben zusammen ein Cosinussignal mit der Amplitude ${C} \hspace{0.15 cm}\underline{= 1 \text{V}}$. | ||
'''(4)''' Der Maximalwert tritt zum Zeitpunkt ${t} = 0$ auf (hier sind Dreieckimpuls und Cosinussignal maximal): | '''(4)''' Der Maximalwert tritt zum Zeitpunkt ${t} = 0$ auf (hier sind Dreieckimpuls und Cosinussignal maximal): | ||
| − | $$x_{\text{max}} = A + B + C \hspace{0.15 cm}\underline{= 2 \text{V}}.$$ | + | :$$x_{\text{max}} = A + B + C \hspace{0.15 cm}\underline{= +2 \text{V}}.$$ |
Die minimalen Werte von ${x(t)}$ ergeben sich dann, wenn der Dreieckimpuls abgeklungen ist und die Cosinusfunktion den Wert $–\hspace{-0.08 cm}1 \,\text{V}$ liefert: | Die minimalen Werte von ${x(t)}$ ergeben sich dann, wenn der Dreieckimpuls abgeklungen ist und die Cosinusfunktion den Wert $–\hspace{-0.08 cm}1 \,\text{V}$ liefert: | ||
| − | $$x_\text{min} = {B} | + | :$$x_\text{min} = {B} - {C}\hspace{0.15 cm}\underline{ = -2\, \text{V}}.$$ |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 10:04, 16 January 2018
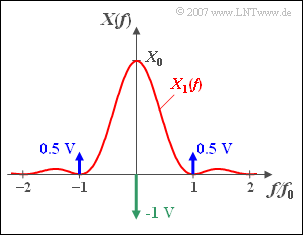
Das skizzierte Spektrum ${X(f)}$ eines Zeitsignals ${x(t)}$ setzt sich zusammen aus
- einem kontinuierlichen Anteil $X_1(f)$,
- dazu drei diracförmigen Spektrallinien.
Der kontinuierliche Anteil lautet mit $f_0 = 200\, \text{kHz}$ und $X_0 = 10^{–5} \text{V/Hz}$:
- $$X_1( f ) = X_0 \cdot {\mathop{\rm si}\nolimits} ^2 ( {\pi {f}/{f_0}} ),\quad {\rm wobei}\quad {\mathop{\rm si}\nolimits} (x) = {\sin (x)}/{x}.$$
Die Spektrallinie bei $f = 0$ hat das Gewicht $–\hspace{-0.08cm}1\,\text{V}$. Daneben gibt es noch zwei Linien bei den Frequenzen $\pm f_0$, beide mit dem Gewicht $0.5\,\text{V}$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Fouriertransformation und -rücktransformation.
- Weitere Informationen zu dieser Thematik liefert das Lernvideo Kontinuierliche und diskrete Spektren.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Als bekannt vorausgesetzt werden kann, dass ein um $t = 0$ symmetrischer Dreieckimpuls $y(t)$ mit der Amplitude ${A}$ und der absoluten Dauer $2T$ (das heißt: die Signalwerte sind nur zwischen $–T$ und $+T$ ungleich $0$) folgende Spektralfunktion besitzt:
- $$Y( f ) = A \cdot T \cdot {\rm si}^2 ( \pi f T ).$$
Fragebogen
Musterlösung
(1) Die einseitige Dauer des symmetrischen Dreieckimpulses beträgt $T = 1/f_0\hspace{0.15 cm}\underline{ = 5 \,{\rm \mu s}}$.
Der Spektralwert $X_0 = X_1(f = 0)$ gibt die Impulsfläche von $x_1(t)$ an. Diese ist gleich ${A} \cdot {T}$. Daraus folgt:
- $$A = \frac{X_0 }{T} = \frac{ 10^{-5}\rm V/Hz }{5 \cdot 10^{-6}{\rm s}}\hspace{0.15 cm}\underline{= 2\;{\rm V}}.$$
(2) Der Gleichsignalanteil ist durch das Diracgewicht bei $f = 0$ gegeben. Man erhält ${B} \hspace{0.15 cm}\underline{= -1 \,\text{V}}$.
(3) Die beiden Spektrallinien bei $\pm f_0$ ergeben zusammen ein Cosinussignal mit der Amplitude ${C} \hspace{0.15 cm}\underline{= 1 \text{V}}$.
(4) Der Maximalwert tritt zum Zeitpunkt ${t} = 0$ auf (hier sind Dreieckimpuls und Cosinussignal maximal):
- $$x_{\text{max}} = A + B + C \hspace{0.15 cm}\underline{= +2 \text{V}}.$$
Die minimalen Werte von ${x(t)}$ ergeben sich dann, wenn der Dreieckimpuls abgeklungen ist und die Cosinusfunktion den Wert $–\hspace{-0.08 cm}1 \,\text{V}$ liefert:
- $$x_\text{min} = {B} - {C}\hspace{0.15 cm}\underline{ = -2\, \text{V}}.$$