Aufgaben:Exercise 3.6Z: Complex Exponential Function

• Return to book

komplexe Exponentialfunktion, Cosinus und Sinus (alle im Spektralbereich)

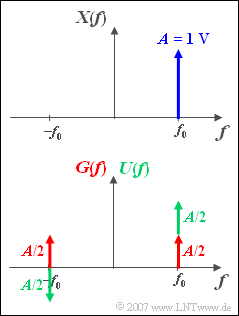
In Zusammenhang mit den Bandpass-Systemen wird oft mit einseitigen Spektren gearbeitet. In der Abbildung sehen Sie eine solche einseitige Spektralfunktion ${X(f)}$, die ein komplexes Zeitsignal ${x(t)}$ zur Folge hat.

In der unteren Skizze ist ${X(f)}$ in einen – bezüglich der Frequenz – geraden Anteil ${G(f)}$ sowie einen ungeraden Anteil ${U(f)}$ aufgespaltet.

Hinweise:

• Die Aufgabe gehört zum Kapitel Gesetzmäßigkeiten der Fouriertransformation.
• Alle dort dargelegten Gesetzmäßigkeiten werden im Lernvideo Gesetzmäßigkeiten der Fouriertransformation an Beispielen verdeutlicht.
• Lösen Sie diese Aufgabe mit Hilfe des Zuordnungssatzes und des Verschiebungssatzes.
• Verwenden Sie für die beiden ersten Teilaufgaben die Signalparameter $A = 1\, \text{V}$ und $f_0 = 125 \,\text{kHz}.$
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Wie lautet die zu $G(f)$ passende Zeitfunktion $g(t)$? Wie groß ist $g(t = 1 \, \mu \text {s})$?

$\text{Re}[g(t = 1 \, \mu \text {s})] \ = \ $  $\text{V}$

$\text{Im}[g(t = 1 \, \mu \text {s})]\ = \ $  $\text{V}$

2

Wie lautet die zu $U(f)$ passende Zeitfunktion $u(t)$? Wie groß ist $u(t = 1 \, \mu \text {s})$?

$\text{Re}[u(t = 1 \, \mu \text {s})]\ = \ $  $\text{V}$

$\text{Im}[g(t = 1 \, \mu \text {s})]\ = \ $  $\text{V}$

3

Welche der Aussagen sind bezüglich des Signals $x(t)$ zutreffend?

	Das Signal lautet $x(t) = A \cdot {\rm e}^{{\rm j}2\pi f_0 t}$.
	In der komplexen Ebene dreht $x(t)$ im Uhrzeigersinn.
	In der komplexen Ebene dreht $x(t)$ entgegen dem Uhrzeigersinn.
	Für eine Umdrehung wird eine Mikrosekunde benötigt.

Musterlösung

Solution

1. $G(f)$ ist die Spektralfunktion eines Cosinussignals mit der Periodendauer $T_0 = 1/f_0 = 8 \, \mu\text {s}$:

$$g( t ) = A \cdot \cos ( {2{\rm{\pi }}f_0 t} ).$$

Bei $t = 1 \, \mu\text {s}$ ist der Signalwert gleich $A \cdot \cos(\pi /4)$:

• Realteil $\text{Re}[g(t = 1 \, \mu \text {s})] = \;\underline{0.707\, \text{V}}$,
• Imaginärteil $\text{Im}[g(t = 1 \, \mu \text {s})] = \;\underline{0.}$.

2. Ausgehend von der Fourierkorrespondenz

$$A \cdot {\rm \delta} ( f )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, A$$

erhält man durch zweimalige Anwendung des Verschiebungssatzes (im Frequenzbereich):

$$U( f ) = {A}/{2} \cdot \delta ( {f - f_0 } ) - {A}/{2} \cdot \delta ( {f + f_0 } )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, u( t ) = {A}/{2} \cdot \left( {{\rm{e}}^{{\rm{j}}2{\rm{\pi }}f_0 t} - {\rm{e}}^{{\rm{ - j}}2{\rm{\pi }}f_0 t} } \right).$$

Nach dem Satz von Euler kann hierfür auch geschrieben werden:

$$u( t ) = {\rm{j}} \cdot A \cdot \sin ( {2{\rm{\pi }}f_0 t} ).$$

• Der Realteil dieses Signals ist stets $0$.
• Bei $t = 1 \, \mu\text {s}$ gilt für den Imaginärteil: $\text{Im}[g(t = 1 \, \mu \text {s})] = \;\underline{0.707\, \text{V}}$.

3. Wegen $X(f) = G(f) + U(f)$ gilt auch:

$$x(t) = g(t) + u(t) = A \cdot \cos ( {2{\rm{\pi }}f_0 t} ) + {\rm{j}} \cdot A \cdot \sin( {2{\rm{\pi }}f_0 t} ).$$

Dieses Ergebnis kann mit dem Satz von Euler wie folgt zusammengefasst werden:

$$x(t) = A \cdot {\rm{e}}^{{\rm{j}}2{\rm{\pi }}f_0 t} .$$

Richtig sind die vorgegebenen Alternativen 1 und 3.

• Das Signal dreht in der komplexen Ebene in mathematisch positiver Richtung, also entgegen dem Uhrzeigersinn.
• Für eine Umdrehung benötigt der „Zeiger” die Periodendauer $T_0 = 1/f_0 = 8 \, \mu\text {s}$.