Difference between revisions of "Aufgaben:Exercise 3.8: Rate Compatible Punctured Convolutional Codes"
m (Guenter verschob die Seite Aufgabe 3.8: RCPC–Codes: Rate Compatible Punctured Convolutional Codes nach Aufgabe 3.8: Rate Compatible Punctured Convolutional Codes) |
|||
| Line 2: | Line 2: | ||
[[File:P_ID2708__KC_A_3_8.png|right|frame|RCPC–Punktierungsmatrizen]] | [[File:P_ID2708__KC_A_3_8.png|right|frame|RCPC–Punktierungsmatrizen]] | ||
| − | Eine wichtige Anwendung für [[Kanalcodierung/Codebeschreibung_mit_Zustands%E2%80%93_und_Trellisdiagramm#Punktierte_Faltungscodes| punktierte Faltungscodes]] sind die <i>Rate Compatible Punctured Convolutional Codes</i> (oder kurz RCPC–Codes), die | + | Eine wichtige Anwendung für [[Kanalcodierung/Codebeschreibung_mit_Zustands%E2%80%93_und_Trellisdiagramm#Punktierte_Faltungscodes| punktierte Faltungscodes]] sind die <i>Rate Compatible Punctured Convolutional Codes</i> (oder kurz RCPC–Codes), die von [[Biografien_und_Bibliografien/Lehrstuhlinhaber_des_LNT#Prof._Dr.-Ing._Dr.-Ing._E.h._Joachim_Hagenauer_.281993-2006.29|Joachim Hagenauer]] in [Hag88] vorgeschlagen wurden. Ausgehend von einem Muttercode $\mathcal{C}_0$ mit der Rate $R_0 = 1/n$ werden durch verschiedene Punktierungsmatrizen $\mathbf{P}_l$ andere Codes $\mathcal{C}_l$ mit höherer Coderate $R_l > R_0$ festgelegt. |
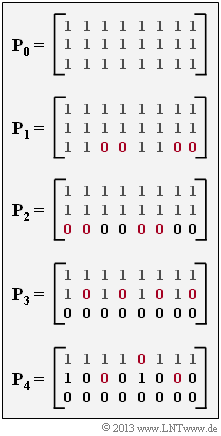
| − | Rechts sind die zu analysierenden Punktierungsmatrizen $\mathbf{P}_0, \ ... \ , \ \mathbf{P}_4$ dargestellt. Ist bei der Matrix $\mathbf{P}_l$ das Matrixelement $P_{ij} = 1$, so wird das entsprechende Codebit übertragen, während $P_{ij} = 0$ auf eine Punktierung hinweist. Im Fragebogen verwenden wir für das Element $P_{ij}$ der Matrix $\mathbf{P}_l$ auch die kürzere Schreibweise $P_{ij}^{(l)}$. | + | Rechts sind die zu analysierenden Punktierungsmatrizen $\mathbf{P}_0, \hspace{0.05cm}\text{ ...} \hspace{0.05cm} , \ \mathbf{P}_4$ dargestellt. |
| + | *Ist bei der Matrix $\mathbf{P}_l$ das Matrixelement $P_{ij} = 1$, so wird das entsprechende Codebit übertragen, während $P_{ij} = 0$ auf eine Punktierung hinweist. | ||
| + | *Im Fragebogen verwenden wir für das Element $P_{ij}$ der Matrix $\mathbf{P}_l$ auch die kürzere Schreibweise $P_{ij}^{(l)}$. | ||
| − | In | + | |
| + | In derGrafik sind alle die Nullen in der Matrix $\mathbf{P}_l$ rot markiert, die in der Matrix $\mathbf{P}_{l–1}$ noch Einsen waren. Durch diese Maßnahme wird die Coderate $R_{l–1}$ gegenüber $R_l$ vergrößert. | ||
Die RCPC–Codes eignen sich gut zur Realisierung von | Die RCPC–Codes eignen sich gut zur Realisierung von | ||
* <i>ungleichem Fehlerschutz</i> für hybride ARQ–Verfahren, | * <i>ungleichem Fehlerschutz</i> für hybride ARQ–Verfahren, | ||
| − | * Systemen mit <i>inkrementeller Redundanz</i> | + | * Systemen mit <i>inkrementeller Redundanz</i>. |
| − | |||
| − | + | Unter „Systemen mit inkrementeller Redundanz” versteht man, dass nach der herkömmlichen Faltungscodierung aus dem Codewort $\underline{x}^{(0)}$ Bits entsprechend der Punktierungsmatrix $\mathbf{P}_l$ weggelassen werden und das verkürzte Codewort $\underline{x}^{(l)}$ übertragen wird: | |
| − | Unter | + | *Kann das punktierte Codewort im Empfänger nicht korrekt decodiert werden, fordert der Empfänger vom Sender weitere Redundanz in Form der zuvor auspunktierten Bits an. |
| + | *Somit wird die Übertragung von nicht benötigter Redundanz verhindert und der Durchsatz an die Kanalgegebenheiten angepasst. | ||
| + | [[File:P_ID2709__hagenauer_kleiner.jpg|left|frame|Joachim Hagenauer]] | ||
| + | ''Hinweise:'' | ||
| + | * Die Aufgabe bezieht sich auf den Abschnitt [[Kanalcodierung/Codebeschreibung_mit_Zustands%E2%80%93_und_Trellisdiagramm#Punktierte_Faltungscodes|Punktierte Faltungscodes]] im Kapitel „Codebeschreibung mit Zustands– und Trellisdiagramm”. | ||
| + | * Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| + | *Die Literaturstelle [Hag88] verweist auf das Paper „Hagenauer, J.: ''Rate Compatible Punctured Convolutional Codes (RCPC codes) and their Applications''. In: IEEE Transactions on Communications, vol COM-36, S. 389 - 400, 1988”. | ||
| + | * Professor [[Biografien_und_Bibliografien/Lehrstuhlinhaber_des_LNT#Prof._Dr.-Ing._Dr.-Ing._E.h._Joachim_Hagenauer_.281993-2006.29| Joachim Hagenauer]] war von 1993 bis 2006 Leiter des Lehrstuhls für Nachrichtentechnik (LNT) der Technischen Universität München. Die Initiatoren des von Ihnen gerade genutzten Lerntutorials – Günter Söder und Klaus Eichin – danken ihrem langjährigen Chef für die Unterstützung und Förderung unseres LNTwww–Projekts während der ersten Jahre. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Line 44: | Line 44: | ||
{Welche Coderaten weisen die Codes $C_1, \ ... \ , \ C_4$ auf? | {Welche Coderaten weisen die Codes $C_1, \ ... \ , \ C_4$ auf? | ||
|type="{}"} | |type="{}"} | ||
| − | ${\rm Matrix \ P_1} \Rightarrow {\rm Code \ | + | ${\rm Matrix \ P_1} \Rightarrow {\rm Code \ \mathcal{C}_1} \text{:} \, R_1 \ = \ ${ 0.4 3% } |
| − | ${\rm Matrix \ P_2} \Rightarrow {\rm Code \ | + | ${\rm Matrix \ P_2} \Rightarrow {\rm Code \ \mathcal{C}_2} \text{:} \, R_2 \ = \ ${ 0.5 3% } |
| − | ${\rm Matrix \ P_3} \Rightarrow {\rm Code \ | + | ${\rm Matrix \ P_3} \Rightarrow {\rm Code \ \mathcal{C}_3} \text{:} \, R_3 \ = \ ${ 0.667 3% } |
| − | ${\rm Matrix \ P_4} \Rightarrow {\rm Code \ | + | ${\rm Matrix \ P_4} \Rightarrow {\rm Code \ \mathcal{C}_4} \text{:} \, R_4 \ = \ ${ 0.889 3% } |
{Welche Aussagen gelten für die Matrixelemente $P_{ij}^{(l)}$? | {Welche Aussagen gelten für die Matrixelemente $P_{ij}^{(l)}$? | ||
Revision as of 15:02, 22 January 2018
Eine wichtige Anwendung für punktierte Faltungscodes sind die Rate Compatible Punctured Convolutional Codes (oder kurz RCPC–Codes), die von Joachim Hagenauer in [Hag88] vorgeschlagen wurden. Ausgehend von einem Muttercode $\mathcal{C}_0$ mit der Rate $R_0 = 1/n$ werden durch verschiedene Punktierungsmatrizen $\mathbf{P}_l$ andere Codes $\mathcal{C}_l$ mit höherer Coderate $R_l > R_0$ festgelegt.
Rechts sind die zu analysierenden Punktierungsmatrizen $\mathbf{P}_0, \hspace{0.05cm}\text{ ...} \hspace{0.05cm} , \ \mathbf{P}_4$ dargestellt.
- Ist bei der Matrix $\mathbf{P}_l$ das Matrixelement $P_{ij} = 1$, so wird das entsprechende Codebit übertragen, während $P_{ij} = 0$ auf eine Punktierung hinweist.
- Im Fragebogen verwenden wir für das Element $P_{ij}$ der Matrix $\mathbf{P}_l$ auch die kürzere Schreibweise $P_{ij}^{(l)}$.
In derGrafik sind alle die Nullen in der Matrix $\mathbf{P}_l$ rot markiert, die in der Matrix $\mathbf{P}_{l–1}$ noch Einsen waren. Durch diese Maßnahme wird die Coderate $R_{l–1}$ gegenüber $R_l$ vergrößert.
Die RCPC–Codes eignen sich gut zur Realisierung von
- ungleichem Fehlerschutz für hybride ARQ–Verfahren,
- Systemen mit inkrementeller Redundanz.
Unter „Systemen mit inkrementeller Redundanz” versteht man, dass nach der herkömmlichen Faltungscodierung aus dem Codewort $\underline{x}^{(0)}$ Bits entsprechend der Punktierungsmatrix $\mathbf{P}_l$ weggelassen werden und das verkürzte Codewort $\underline{x}^{(l)}$ übertragen wird:
- Kann das punktierte Codewort im Empfänger nicht korrekt decodiert werden, fordert der Empfänger vom Sender weitere Redundanz in Form der zuvor auspunktierten Bits an.
- Somit wird die Übertragung von nicht benötigter Redundanz verhindert und der Durchsatz an die Kanalgegebenheiten angepasst.
Hinweise:
- Die Aufgabe bezieht sich auf den Abschnitt Punktierte Faltungscodes im Kapitel „Codebeschreibung mit Zustands– und Trellisdiagramm”.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Die Literaturstelle [Hag88] verweist auf das Paper „Hagenauer, J.: Rate Compatible Punctured Convolutional Codes (RCPC codes) and their Applications. In: IEEE Transactions on Communications, vol COM-36, S. 389 - 400, 1988”.
- Professor Joachim Hagenauer war von 1993 bis 2006 Leiter des Lehrstuhls für Nachrichtentechnik (LNT) der Technischen Universität München. Die Initiatoren des von Ihnen gerade genutzten Lerntutorials – Günter Söder und Klaus Eichin – danken ihrem langjährigen Chef für die Unterstützung und Förderung unseres LNTwww–Projekts während der ersten Jahre.
Fragebogen
Musterlösung
(2) Für die Rate des Codes $C_l = p/N_l$, wobei $N_l$ die Anzahl aller Einsen in der Punktierungsmatrix $\mathbf{P}_l$ und $p$ die Punktierungsperiode bezeichnet:
- $R_0 = 8/24 = 1/3 = \underline{0.333}$,
- $R_1 = 8/20 = 2/5 = \underline{0.400}$,
- $R_2 = 8/16 = 1/2 = \underline{0.500}$,
- $R_3 = 8/12 = 2/3 = \underline{0.667}$,
- $R_4 = 8/9 = \underline{0.889}$.
(3) Alle Einsen in der Matrix $\mathbf{P}_4$ sind auch in den darüber liegenden Matrizen $\mathbf{P}_3, \ ... \ , \ \mathbf{P}_0$ enthalten. In der Matrix $\mathbf{P}_3$ kommen gegenüber $\mathbf{P}_4$ drei Einsen hinzu, in der Matrix $\mathbf{P}_2$ gegenüber $\mathbf{P}_3$ nochmals vier, usw. ⇒ Richtig sind die Lösungsvorschläge 1 und 4.