Aufgaben:Exercise 1.3Z: Exponentially Decreasing Impulse Response

• Return to book

Exponentiell abfallende Impulsantwort

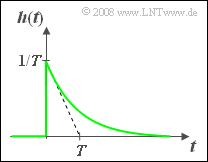
Gemessen wurde die Impulsantwort $h(t)$ eines LZI–Systems, die für alle Zeiten $t < 0$ identisch $0$ ist und für $t > 0$ entsprechend einer Exponentialfunktion abfällt:

$$h(t) = {1}/{T} \cdot {\rm e}^{-t/T}.$$

Der Funktionsparameter sei $T = 1 \ \rm ms$. In der Teilaufgabe (3) ist nach der 3dB–Grenzfrequenz $f_{\rm G}$ gefragt, die wie folgt implizit definiert ist:

$$|H(f = f_{\rm G})| = {1}/{\sqrt{2}} \cdot|H(f = 0)| .$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Systembeschreibung im Zeitbereich
• Gegeben ist das folgende bestimmte Integral:

$$\int_{ 0 }^{ \infty } \frac{1}{1+x^2} \hspace{0.1cm}{\rm d}x = {\pi}/{2} .$$

• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Berechnen Sie den Frequenzgang $H(f)$. Welcher Wert ergibt sich für $f = 0$?

$H(f = 0) \ = \ $

2

Welchen Wert besitzt die Impulsantwort zur Zeit $t = 0$?

$h(t = 0) \ = \ $  $\rm 1/s$

3

Berechnen Sie die 3dB–Grenzfrequenz $f_{\rm G}$.

$f_{\rm G} \ =\ $  $\rm Hz$

4

Welche der folgenden Aussagen sind zutreffend?

	Das betrachtete System ist kausal.
	Das betrachtete System hat Hochpass–Charakter.
	Liegt am Systemeingang ein Cosinussignal der Frequenz $f_{\rm G}$ an, so ist das Ausgangssignal ebenfalls cosinusförmig.

Musterlösung

Solution

(1)  Der Frequenzgang $H(f)$ ist die Fouriertransformierte von $h(t)$:

$$H(f) = \int_{-\infty}^{+\infty}h(t) \cdot {\rm e}^{\hspace{0.05cm}{-\rm j}2\pi ft}\hspace{0.15cm} {\rm d}t = \frac{1}{T} \cdot \int_{0}^{+\infty} {\rm e}^{\hspace{0.05cm}{-(\rm j}2\pi f+ {1}/{T}) t}\hspace{0.15cm} {\rm d}t.$$

Die Integration führt zum Ergebnis:

$$H(f) = \left[ \frac{-1/T}{{\rm j}2\pi f+{1}/{T}} \cdot {\rm e}^{\hspace{0.05cm}{-(\rm j}2\pi f+ {1}/{T}) t}\right]_{0}^{\infty}= \frac{1}{1+{\rm j} \cdot 2\pi fT}.$$

Bei der Frequenz $f = 0$ hat der Frequenzgang den Wert $H(f = 0) \; \underline{= 1}$.

(2)  Dieser Frequenzgang kann mit Real– und Imaginärteil auch wie folgt geschrieben werden:

$$H(f) = \frac{1}{1+(2\pi fT)^2} -{\rm j} \cdot \frac{2\pi fT}{1+(2\pi fT)^2}.$$

Die Impulsantwort an der Stelle $t = 0$ ist gleich dem Integral über $H(f)$. Da der Imaginärteil ungerade ist, muss nur über den Realteil integriert werden. Unter Ausnutzung der Symmetrieeigenschaft erhält man:

$$h(t=0)=2 \cdot \int_{ 0 }^{ \infty } \frac{1}{1+(2\pi fT)^2} \hspace{0.1cm}{\rm d}f = \frac{1}{\pi T} \cdot \int_{ 0 }^{ \infty } \frac{1}{1+x^2} \hspace{0.1cm}{\rm d}x .$$

Unter Benutzung des angegebenen bestimmten Integrals mit dem Resultat $π/2$ ergibt sich:

$$h(t=0)= \frac{1}{2 T} \hspace{0.15cm}\underline{= {\rm 500\cdot 1/s}}.$$

Dieses Ergebnis zeigt auch, dass die Impulsantwort bei $t = 0$ gleich dem Mittelwert aus dem links– und dem rechtsseitigen Grenzwert ist.

(3)  Der Amplitudengang lautet bei dieser Aufgabe bzw. allgemein mit der 3dB-Grenzfrequenz $f_{\rm G}$:

$$|H(f)| = \frac{1}{\sqrt{1+(2\pi fT)^2}} = \frac{1}{\sqrt{1+(f/f_{\rm G})^2}}.$$

Durch Koeffizientenvergleich erhält man:

$$f_{\rm G} = \frac{1}{2\pi T} \hspace{0.15cm}\underline{= {\rm 159 \hspace{0.1cm} Hz}}.$$

(4)  Richtig ist der erste Lösungsvorschlag}.:

• Wegen $h(t) = 0$ für $t < 0$ ist das System tatsächlich kausal. Es handelt sich um einen Tiefpass erster Ordnung.
• Dagegen müsste ein Hochpass folgende Bedingung erfüllen:

$$H(f = 0) = \int_{-\infty}^{+\infty}h(t) \hspace{0.15cm}{\rm d}t = 0.$$

• $H(f)$ ist eine komplexe Funktion. Der Phasengang lautet (siehe Aufgabe 1.1Z):

$$b(f) = \arctan {f}/{f_{\rm G}}.$$

• Für die Frequenz $f = f_{\rm G}$ erhält man $b(f = f_{\rm G}) = π/4 = 45^\circ$.
• Liegt am Eingang ein Cosinussignal der Frequenz $f = f_{\rm G}$ an, so ergibt sich für das Ausgangssignal:

$$y(t) = K \cdot \cos( 2 \pi f_{\rm G} t - 45^{\circ}).$$

• Dieses Signal ist zwar eine harmonische Schwingung, aber kein Cosinussignal.