Difference between revisions of "Applets:Attenuation of Copper Cables"
| Line 85: | Line 85: | ||
:$$H_{\rm K}(f) · H_{\rm E}(f) = H_{\rm CRO}(f).$$ | :$$H_{\rm K}(f) · H_{\rm E}(f) = H_{\rm CRO}(f).$$ | ||
| − | This means: The [[Digitalsignalübertragung/Eigenschaften_von_Nyquistsystemen#Erstes_Nyquistkriterium_im_Frequenzbereich| | + | This means: The [[Digitalsignalübertragung/Eigenschaften_von_Nyquistsystemen#Erstes_Nyquistkriterium_im_Frequenzbereich|first Nyquist criterion]] is met ⇒ <br>Timely successive impulses do not disturb each other ⇒ there are no [[Digitalsignalübertragung/Ursachen_und_Auswirkungen_von_Impulsinterferenzen|Intersymbol Interferences]]. |
| − | + | In the case of white noise, the transmission quality is thus determined solely by the noise power in front of the receiver: | |
:$$P_{\rm N} =\frac{N_0}{2} \cdot \int_{-\infty}^{+\infty} |H_{\rm E}(f)|^2 \ {\rm d}f\hspace{1cm}\text{mit}\hspace{1cm}|H_{\rm E}(f)|^2 = \frac{|H_{\rm CRO}(f)|^2}{|H_{\rm K}(f)|^2}.$$ | :$$P_{\rm N} =\frac{N_0}{2} \cdot \int_{-\infty}^{+\infty} |H_{\rm E}(f)|^2 \ {\rm d}f\hspace{1cm}\text{mit}\hspace{1cm}|H_{\rm E}(f)|^2 = \frac{|H_{\rm CRO}(f)|^2}{|H_{\rm K}(f)|^2}.$$ | ||
| − | + | The lowest possible noise performance results with an ideal channel ⇒ $H_{\rm K}(f) \equiv 1$ and a rectangular $H_{\rm CRO}(f) \equiv 1$ in $|f| \le f_{\rm Nyq}$: | |
| − | :$$P_\text{N, min} = P_{\rm N} \ \big [\text{ | + | :$$P_\text{N, min} = P_{\rm N} \ \big [\text{optimal system: }H_{\rm K}(f) \equiv 1, \ r=0 \big ] = N_0 \cdot f_{\rm Nyq} .$$ |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
Revision as of 01:01, 7 March 2018
Contents
Applet Description
Theoretical Background
Magnitude Frequency Response and Attenuation Function
Following relationship exists between the magnitude frequency response and the attenuation function:
- $$\left | H_{\rm K}(f)\right |=10^{-a_\text{K}(f)/20} = {\rm e}^{-a_\text{K, Np}(f)}.$$
- The index „K” makes it clear, that the considered LTI system is a cable(Ger: Kabel).
- For the first calculation rule, the damping function $a_\text{K}(f)$ must be used in $\rm dB$ (decibel).
- For the first calculation rule, the damping function $a_\text{K, Np}(f)$ must be used in $\rm Np$ (Neper).
- The following conversions apply: $\rm 1 \ dB = 0.05 \cdot \ln (10) \ Np= 0.1151 \ Np$ or $\rm 1 \ Np = 20 \cdot \lg (e) \ dB= 8.6859 \ dB$.
- This applet exclusively uses dB values.
Attenuation Function of a Coaxial Cable
According to [Wel77][1] the Attenuation Function of a Coaxial Cable of length $l$ is given as follows:
- $$a_{\rm K}(f)=(\alpha_0+\alpha_1\cdot f+\alpha_2\cdot \sqrt{f}) \cdot l.$$
- It is important to note the difference between $a_{\rm K}(f)$ in $\rm dB$ and the „alpha” coefficient with other pseudo–units.
- The attenuation function $a_{\rm K}(f)$ is directly proportional to the cable length $l$; $a_{\rm K}(f)/l$ is referred to as the „attenuation factor” or „kilometric attenuation”.
- The frequency-independent component $α_0$ of the attenuation factor takes into account the Ohmic losses.
- The frequency proportional portion $α_1 · f$ of the attenuation factor is due to the derivation losses („crosswise loss”) .
- the dominant portion $α_2$ goes back to Skineffekt, which causes a lower current density inside the conductor compared to its surface. As a result, the resistance of an electric line increases with the square root of the frequency.
The constants for the standard coaxial cable with a 2.6 mm inner diameter and a 9.5 mm outer diameter ⇒ short Coax (2.6/9.5 mm) are:
- $$\alpha_0 = 0.014\, \frac{ {\rm dB} }{ {\rm km} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_1 = 0.0038\, \frac{ {\rm dB} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 2.36\, \frac{ {\rm dB} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}.$$
The same applies to the coaxial coaxial cable' ⇒ short Coax (1.2/4.4 mm):
- $$\alpha_0 = 0.068\, \frac{ {\rm dB} }{ {\rm km} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_1 = 0.0039\, \frac{ {\rm dB} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 =5.2\, \frac{ {\rm dB} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}.$$
These values can be calculated from the cables' geometric dimensions and have been confirmed by measurements at the Fernmeldetechnisches Zentralamt in Darmstadt – see [Wel77][1] . They are valid for a temperature of 20 ° C (293 K) and frequencies greater than 200 kHz.
Attenuation Function of a Two–wired Line
According to [PW95][2] the attenuation function of a Two–wired Line of length $l$ is given as follows:
- $$a_{\rm K}(f)=(k_1+k_2\cdot (f/{\rm MHz})^{k_3}) \cdot l.$$
This function is not directly interpretable, but is a phenomenological description.
[PW95][2]also provides the constants determined by measurement results:
- $d = 0.35 \ {\rm mm}$: $k_1 = 7.9 \ {\rm dB/km}, \hspace{0.2cm}k_2 = 15.1 \ {\rm dB/km}, \hspace{0.2cm}k_3 = 0.62$,
- $d = 0.40 \ {\rm mm}$: $k_1 = 5.1 \ {\rm dB/km}, \hspace{0.2cm}k_2 = 14.3 \ {\rm dB/km}, \hspace{0.2cm}k_3 = 0.59$,
- $d = 0.50 \ {\rm mm}$: $k_1 = 4.4 \ {\rm dB/km}, \hspace{0.2cm}k_2 = 10.8 \ {\rm dB/km}, \hspace{0.2cm}k_3 = 0.60$,
- $d = 0.60 \ {\rm mm}$: $k_1 = 3.8 \ {\rm dB/km}, \hspace{0.2cm}k_2 = \hspace{0.25cm}9.2 \ {\rm dB/km}, \hspace{0.2cm}k_3 = 0.61$.
From these numerical values one recognizes:
- The attenuation factor $α(f)$ and the attenuation function $a_{\rm K}(f) = α(f) · l$ depend significantly on the pipe diameter. The cables laid since 1994 with $d = 0.35 \ \rm (mm)$ and $d = 0.5$ mm have a 10% greater attenuation factor than the older lines with $d = 0.4$ or $d= 0.6$.
- However, this smaller diameter, which is based on the manufacturing and installation costs, significantly reduces the range $l_{\rm max}$ of the transmission systems used on these lines, so that in the worst case scenario expensive intermediate generators have to be used.
- The current transmission methods for copper lines prove only a relatively narrow frequency band, for example $120\ \rm kHz$ with ISDN and ca. $1100 \ \rm kHz$ with DSL. For $f = 1 \ \rm MHz$ the attenuation factor of a 0.4 mm cable is around $20 \ \rm dB/km$, so that even with a cable length of $l = 4 \ \rm km$ the Attenuation does not exceed $80 \ \rm dB$.
Conversion Between $k$ and $\alpha$ parameters
The $k$–parameters of the attenuation factor ⇒ $\alpha_{\rm I} (f)$ can be converted into corresponding $\alpha$–parameters ⇒ $\alpha_{\rm II} (f)$:
- $$\alpha_{\rm I} (f) = k_1 + k_2 \cdot (f/f_0)^{k_3}\hspace{0.05cm}, \hspace{0.2cm}{\rm mit} \hspace{0.15cm} f_0 = 1\,{\rm MHz},$$
- $$\alpha_{\rm II} (f) = \alpha_0 + \alpha_1 \cdot f + \alpha_2 \cdot \sqrt {f}.$$
As a criterion of this conversion, we assume that the quadratic deviation of these two functions is minimal within a bandwidth $B$:
- $$\int_{0}^{B} \left [ \alpha_{\rm I} (f) - \alpha_{\rm II} (f)\right ]^2 \hspace{0.1cm}{\rm d}f \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Minimum} \hspace{0.05cm} .$$
It is obvious that $α_0 = k_1$. The parameters $α_1$ and $α_2$ are dependent on the underlying bandwidth $B$ and are:
- $$\begin{align*}\alpha_1 & = 15 \cdot (B/f_0)^{k_3 -1}\cdot \frac{k_3 -0.5}{(k_3 + 1.5)(k_3 + 2)}\cdot {k_2}/{ {f_0} }\hspace{0.05cm} ,\\ \alpha_2 & = 10 \cdot (B/f_0)^{k_3 -0.5}\cdot \frac{1-k_3}{(k_3 + 1.5)(k_3 + 2)}\cdot {k_2}/{\sqrt{f_0} }\hspace{0.05cm} .\end{align*}$$
$\text{Example 1:}$
- For $k_3 = 1$ (frequency proportional attenuation factor) we get $\alpha_0 = k_0\hspace{0.05cm} ,\hspace{0.2cm} \alpha_1 = {k_2}/{ {f_0} }\hspace{0.05cm} ,\hspace{0.2cm} \alpha_2 = 0\hspace{0.05cm} .$
- For $k_3 = 0.5$ (Skin effect) we get the coefficients: $\alpha_0 = k_0\hspace{0.05cm} ,\hspace{0.2cm}\alpha_1 = 0\hspace{0.05cm} ,\hspace{0.2cm} \alpha_2 = {k_2}/{\sqrt{f_0} }\hspace{0.05cm}.$
- For $k_3 < 0.5$ we get a negative $\alpha_1$. Conversion is only possible for $0.5 \le k_3 \le 1$.
Umrechnung in Gegenrichtung
Fehlt noch
Channel Influence on the Binary Nyquistent Equalization
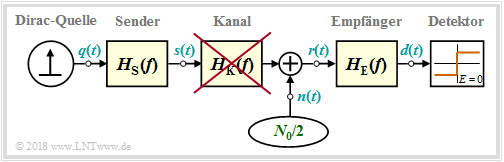
Going by the block diagram: Between the Dirac source and the decider are the frequency responses for the transmitter ⇒ $H_{\rm S}(f)$, Channel ⇒ $H_{\rm K}(f)$ and receiver ⇒ $H_{\rm E}(f)$.
In this applet
- we neglect the influence of the transmitted pulse form ⇒ $H_{\rm S}(f) \equiv 1$ ⇒ dirac shaped transmission signal $s(t)$,
- presuppose a binary Nyquist system with cosine–roll-off around the Nyquistf requency $f_{\rm Nyq} = [f_1 + f_2]/2 =1(2T)$ :
- $$H_{\rm K}(f) · H_{\rm E}(f) = H_{\rm CRO}(f).$$
This means: The first Nyquist criterion is met ⇒
Timely successive impulses do not disturb each other ⇒ there are no Intersymbol Interferences.
In the case of white noise, the transmission quality is thus determined solely by the noise power in front of the receiver:
- $$P_{\rm N} =\frac{N_0}{2} \cdot \int_{-\infty}^{+\infty} |H_{\rm E}(f)|^2 \ {\rm d}f\hspace{1cm}\text{mit}\hspace{1cm}|H_{\rm E}(f)|^2 = \frac{|H_{\rm CRO}(f)|^2}{|H_{\rm K}(f)|^2}.$$
The lowest possible noise performance results with an ideal channel ⇒ $H_{\rm K}(f) \equiv 1$ and a rectangular $H_{\rm CRO}(f) \equiv 1$ in $|f| \le f_{\rm Nyq}$:
- $$P_\text{N, min} = P_{\rm N} \ \big [\text{optimal system: }H_{\rm K}(f) \equiv 1, \ r=0 \big ] = N_0 \cdot f_{\rm Nyq} .$$
$\text{Definitionen:}$
- Als Gütekriterium für ein gegebenes System verwenden wir den Gesamt–Wirkungsgrad:
- $$\eta_\text{K+R} = \frac{P_{\rm N} \ \big [\text{gegebenes System: Kanal }H_{\rm K}(f), \ \text{Roll-off-Faktor }r \big ]}{P_{\rm N} \ \big [\text{optimales System: }H_{\rm K}(f) \equiv 1, \ r=0 \big ]} =\frac{1}{f_{\rm Nyq} } \cdot \int_{0}^{+\infty} \vert H_{\rm E}(f) \vert^2 \ {\rm d}f \le 1.$$
Diese Systemgröße wird im Applet für beide Parametersätze in logarithmierter Form angegeben: $10 \cdot \lg \ \eta_\text{K+R} \le 0 \ \rm dB$.
- Durch Variation und Optimierung des Roll-off-Faktors $r$ erhält man den Kanal–Wirkungsgrad:
- $$\eta_\text{K} = \min_{0 \le r \le 1} \ \eta_\text{K+R} .$$
Ab hier bis zum Beginn der Versuchsdurchführung ist alles Mist - eine Art Vorratsspeicher
- Bei UMTS ist das Empfangsfilter $H_{\rm E}f) = H_{\rm S}(f)$ an den Sender angepasst (Matched–Filter) und der Gesamtfrequenzgang $H(f) = H_{\rm S}(f) · H_{\rm E}(f)$ erfüllt
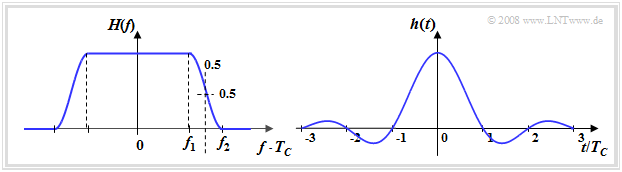
- $$ H(f) = H_{\rm CRO}(f) = \left\{ \begin{array}{c} 1 \\ 0 \\ \cos^2 \left( \frac {\pi \cdot (|f| - f_1)}{2 \cdot (f_2 - f_1)} \right)\end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}}\\ {\rm sonst }\hspace{0.05cm}. \end{array} \begin{array}{*{20}c} |f| \le f_1, \\ |f| \ge f_2,\\ \\\end{array}$$
Die zugehörige Zeitfunktion lautet:
- $$h(t) = h_{\rm CRO}(t) ={\rm si}(\pi \cdot t/ T_{\rm C}) \cdot \frac{\cos(r \cdot \pi t/T_{\rm C})}{1- (2r \cdot t/T_{\rm C})^2}. $$
„CRO” steht hierbei für Cosinus–Rolloff (englisch: Raised Cosine). Die Summe $f_1 + f_2$ ist gleich dem Kehrwert der Chipdauer $T_{\rm C} = 260 \ \rm ns$, also gleich $3.84 \ \rm MHz$. Der Rolloff–Faktor (wir bleiben bei der in $\rm LNTwww$ gewählten Bezeichnung $r$, im UMTS–Standard wird hierfür $\alpha$ verwendet)
- $$r = \frac{f_2 - f_1}{f_2 + f_1} $$
wurde bei UMTS zu $r = 0.22$ festgelegt. Die beiden Eckfrequenzen sind somit
- $$f_1 = {1}/(2 T_{\rm C}) \cdot (1-r) \approx 1.5\,{\rm MHz}, \hspace{0.2cm} f_2 ={1}/(2 T_{\rm C}) \cdot (1+r) \approx 2.35\,{\rm MHz}.$$
Die erforderliche Bandbreite beträgt $B = 2 · f_2 = 4.7 \ \rm MHz$. Für jeden UMTS–Kanal steht somit mit $5 \ \rm MHz$ ausreichend Bandbreite zur Verfügung.
$\text{Fazit:}$ Die Grafik zeigt
- links das (normierte) Nyquistspektrum $H(f)$, und
- rechts den zugehörigen Nyquistimpuls $h(t)$, dessen Nulldurchgänge im Abstand $T_{\rm C}$ äquidistant sind.
$\text{Es ist zu beachten:}$
- Das Sendefilter $H_{\rm S}(f)$ und Matched–Filter $H_{\rm E}(f)$ sind jeweils Wurzel–Cosinus–Rolloff–förmig (englisch: Root Raised Cosine). Erst das Produkt $H(f) = H_{\rm S}(f) · H_{\rm E}(f)$ den Cosinus–Rolloff.
- Das bedeutet auch: Die Impulsantworten $h_{\rm S}(t)$ und $h_{\rm E}(t)$ erfüllen für sich allein die erste Nyquistbedingung nicht. Erst die Kombination aus beiden (im Zeitbereich die Faltung) führt zu den gewünschten äquidistanten Nulldurchgängen.
$$a_k(f)=(k_1+k_2\cdot f^{k_3})\cdot l \hspace{0.5cm}\Rightarrow \hspace{0.5cm} \text{empirische Formel von Pollakowski & Wellhausen.}$$
- Umrechnung der $k$-Parameter in die $a$-Parameter nach dem Kriterium, dass der mittlere quadratische Fehler innerhalb der Bandbreite $B$ minimal sein soll:
$$a_0=k_1 \text{(trivial)}, \quad a_1=15\cdot B^{k_3-1}\cdot \frac{k_2\cdot (k_3-0.5)}{(k_3+1.5)\cdot (k_3+2)}, \quad a_2=10\cdot B^{k_3-0.5}\cdot \frac{k_2\cdot (1-k_3)}{(k_3+1.5)\cdot (k_3+2)}.$$
- Kontrolle: $k_3=1 \Rightarrow a_1=k_2;\ a_2=0 \quad k_3=0.5 \Rightarrow a_1=0;\ a_2=k_2.$
- Der Gesamtfrequenzgang $H(f)$ ist ein Cosinus-Rolloff-Tiefpass mit Rolloff-Faktor $r$, wobei stets $B=f_2$ und $r=\frac{f_2-f_1}{f_2+f_1}$ gelten soll.
- Ohne Berücksichtigung des Sendespektrums gilt $H(f)=H_K(f)\cdot H_E(f) \Rightarrow H_E(f)=\frac{H(f)}{H_K(f)}$.
- Der angegebene Integralwert $=\int_{-\infty}^{+\infty} \left| H_E(f)\right|^2 \hspace{0.15cm} {\rm d}f$ ist ein Maß für die Rauschleistung des Systems, wenn der Kanal $H_K(f)$ durch das Empfangsfilter $H_E(f)$ in weiten Bereichen bis $f_1$ vollständig entzerrt wird.
- idealer Kanal ($a_0=a_1=a_2=0$ dB), $B=20$ MHz, $r=0$: Integralwert = $40$ MHz.
- schwach verzerrender Kanal ($a_2=5$ dB), $B=20$ MHz, $r=0.5$: Integralwert $\approx 505$ MHz.
Versuchsdurchführung
- Wählen Sie zunächst die Nummer 1 ... 6 der zu bearbeitenden Aufgabe.
- Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
- Lösung nach Drücken von „Hide solution”.
- Aufgabenstellung und Lösung in Englisch.
Die Nummer 0 entspricht einem „Reset”:
- Gleiche Einstellung wie beim Programmstart.
- Ausgabe eines „Reset–Textes” mit weiteren Erläuterungen zum Applet.
In der folgenden Beschreibung bedeutet
- Blau: Verteilungsfunktion 1 (im Applet blau markiert),
- Rot: Verteilungsfunktion 2 (im Applet rot markiert).
(1) Setzen Sie Blau zunächst auf $\text{Coax (2.6/9.5 mm)}$ und anschließend auf $\text{Coax (1.2/4.4 mm)}$. Die Kabellänge sei jeweils $l_{\rm Blau}= 3\ \rm km$.
- Betrachten und Interpretieren Sie $a_{\rm K}(f)$ und $\vert H_{\rm K}(f) \vert$, insbesondere die Funktionswerte $a_{\rm K}(f = f_\star = 30 \ \rm MHz)$ und $\vert H_{\rm K}(f = 0) \vert$.
$\Rightarrow\hspace{0.3cm}\text{Näherungsweise steigt die Dämpfungsfunktion mit }\sqrt{f}\text{ und der Betragsfrequenzgang fällt ähnlich einer Exponentialfunktion};$
$\hspace{1.15cm}\text{Coax (2.6/9.5 mm): }a_{\rm K}(f = f_\star) = 39.2\text{ dB;}\hspace{0.5cm}\vert H_{\rm K}(f = 0) \vert = 0.9951;$
$\hspace{1.15cm}\text{Coax (1.2/4.4 mm): }a_{\rm K}(f = f_\star) = 86.0\text{ dB;}\hspace{0.5cm}\vert H_{\rm K}(f = 0) \vert = 0.9768.$
(2) Für Blau gelte $\text{Coax (1.2/4.4 mm)}$ und $l_{\rm Blau} = 3\ \rm km$. Wie wird $a_{\rm K}(f =f_\star = 30 \ \rm MHz)$ von $\alpha_0$, $\alpha_1$ und $\alpha_2$ beeinflusst?
$\Rightarrow\hspace{0.3cm}\text{Entscheidend ist }\alpha_2\text{ (Skineffekt). Die Beiträge von } \alpha_0\text{ (Ohmsche Verluste) und }\alpha_1 \text{ (Querverluste) sind jeweils nur ca. 0.2 dB.}$
(3) Setzen Sie zusätzlich Rot auf $\text{Two–wired Line (0.5 mm)}$ und $l_{\rm Rot} = 3\ \rm km$. Welcher Wert ergibt sich für $a_{\rm K}(f =f_\star= 30 \ \rm MHz)$?
- Bis zu welcher Länge $l_{\rm Rot}$ liegt die rote Dämfungsfunktion unter der blauen?
$\Rightarrow\hspace{0.3cm}\text{Für die rote Kurve gilt: }a_{\rm K}(f = f_\star) = 262.5 {\ \rm dB} \text{. Obige Bedingung wird erfüllt für }l_{\rm Rot} = 0.95\ {\rm km} \ \Rightarrow \ a_{\rm K}(f = f_\star) = ??? {\ \rm dB}.$
(4) Setzen Sie Rot auf $\text{Two–wired Line (0.5 mm)}$ und Blau auf $\text{Conversion of Red}$. Es gelte $l_{\rm Rot} = l_{\rm Blau} = 1\ \rm km$.
- Betrachten und Interpretieren Sie die dargestellten Funktionsverläufe für $a_{\rm K}(f)$ und $\vert H_{\rm K}(f) \vert$.
$\Rightarrow\hspace{0.3cm}\text{Sehr gute Approximation der Zweidrahtleitung durch den blauen Parametersatz, sowohl bezüglich }a_{\rm K}(f) \text{ als auch }\vert H_{\rm K}(f) \vert.$
(5) Es gelten die Einstellungen von (4). Welche Anteile der Dämpfungsfunktion gehen auf Ohmschen Verlust, Querverluste und Skineffekt zurück?
$\Rightarrow\hspace{0.3cm}\text{Lösung anhand '''Blau''': }\alpha_0(f = f_\star= 30 \ {\rm MHz}) = 4 \ {\rm dB/km}, \hspace{0.2cm}\alpha_1(f = f_\star) = 12.8 \ {\rm dB/km}, \hspace{0.2cm}\alpha_2(f = f_\star) = 60.9 \ {\rm dB/km};$
$\hspace{1.15cm}\text{Bei einer Zweidrahtleitung ist der Einfluss der Längs– und der Querverluste signifikant größer als bei einem Koaxialkabel.}$
(6) Variieren Sie ausgehend von der bisherigen Einstellung den Parameter $0.5 \le k_3 \le 1$. Was erkennt man anhand von $a_{\rm K}(f)$ und $\vert H_{\rm K}(f) \vert$?
$\Rightarrow\hspace{0.3cm}\text{Bei festem }k_2\text {wird }a_{\rm K}(f)\text{ immer größer und es ergibt sich für }k_3 = 1\text{ ein linearer Verlauf; }\vert H_{\rm K}(f) \vert \text{ nimmt immer schneller ab;}$
$\hspace{1.15cm}\text{Mit }k_3 \to 0.5\text{ nähert sich die Dämpfungsfunktion der Zweidrahtleitung der eines Koaxialkabels immer mehr an.}$
Vorgeschlagene Parametersätze
(1) Nur blauer Parametersatz, $l=1$ km, $B=30$ MHz, $r=0$, $a_0=20$, $a_1=0$, $a_2=0$:
Konstante Werte $a_K=20$ dB und $\left| H_K(f)\right|=0.1$. Nur Ohmsche Verluste werden berücksichtigt.
(2) Parameter wie (1), aber zusätzlich $a_1=1$ dB/(km · MHz):
Linearer Anstieg von $a_K(f)$ zwischen $20$ dB und $50$ dB, $\left| H_K(f)\right|$ fällt beidseitig exponentiell ab.
(3) Parameter wie (1), aber $a_0=0$, $a_1=0$, $a_2=1$ dB/(km · MHz1/2).
$a_K(f)$ und $\left| H_K(f)\right|$ werden ausschließlich durch den Skineffekt bestimmt. $a_K(f)$ ist proportional zu $f^{1/2}$.
(4) Parameter wie (1), aber nun mit der Einstellung „Koaxialkabel $2.6/9.5$ mm“ (Normalkoaxialkabel):
Es überwiegt der Skineffekt; $a_k$ ($f=30$ MHz)$=13.05$ dB; ohne $a_0$: $13.04$ dB, ohne $a_1=12.92$ dB.
(5) Parameter wie (1), aber nun mit der Einstellung „Koaxialkabel $1.2/4.4$ mm“ (Kleinkoaxialkabel):
Wieder überwiegt der Skineffekt; $a_k$ ($f=30$ MHz)$=28.66$ dB; ohne $a_0$: $28.59$ dB, ohne $a_1=28.48$ dB.
(6) Nur roter Parametersatz, $l=1 km$, $b=30$ MHz, $r=0$, Einstellung „Zweidrahtleitung $0.4$ mm“.
Skineffekt ist auch hier dominant; $a_k$ ($f=30$ MHz)$=111.4$ dB; ohne $k_1$: $106.3$ dB.
(7) Parameter wie (6), aber nun Halbierung der Kabellänge ($l=0.5$ km):
Auch die Dämpfungswerte werden halbiert: $a_k$ ($f=30$ MHz)$=55.7$ dB; ohne $k_1$: $53.2$ dB.
(8) Parameter wie (7), dazu im blauen Parametersatz die umgerechneten Werte der Zweidrahtleitung:
Sehr gute Approximation der $k$-Parameter durch die $a$-Parameter; Abweichung < $0.4$ dB.
(9) Parameter wie (8), aber nun Approximation auf die Bandbreite $B=20$ MHz:
Noch bessere Approximation der $k$-Parameter durch die $a$-Parameter; Abweichung < $0.15$ dB.
(10) Nur blauer Parametersatz, $l=1$ km, $B=30$ MHz, $r=0$, $a_0=a_1=a_2=0$; unten Darstellung $\left| H_K(f)\right|^2$:
Im gesamten Bereich ist $\left| H_K(f)\right|^2=1$; der Integralwert ist somit $2B=60$ (in MHz).
(11) Parameter wie (10), aber nun mit Einstellung „Koaxialkabel $2.6/9.5$ mm“ (Normalkoaxialkabel):
$\left| H_K(f)\right|^2$ ist bei $f=1$ etwa $1$ und steigt zu den Rändern bis ca. $20$. Der Integralwert ist ca. $550$.
(12) Parameter wie (11), aber nun mit der deutlich größeren Kabellänge $l=5$ km:
Deutliche Verstärkung des Effekts; Anstieg bis ca. $3.35\cdot 10^6$ am Rand und Integralwert $2.5\cdot 10^7$.
(13) Parameter wie (12), aber nun mit Rolloff-Faktor $r=0.5$:
Deutliche Abschwächung des Effekts; Anstieg bis ca. $5.25\cdot 10^4$ ($f$ ca. $20$ MHz), Integralwert ca. $1.07\cdot 10^6$.
(14) Parameter wie (13), aber ohne Berücksichtigung der Ohmschen Verluste ($a_0=0$):
Nahezu gleichbleibendes Ergebnis; Anstieg bis ca. $5.15\cdot 10^4$ ($f$ ca. $20$ MHz), Integralwert ca. $1.05\cdot 10^6$.
(15) Parameter wie (14), aber auch ohne Berücksichtigung der Querverluste ($a_1=0$):
Ebenfalls kein großer Unterschied; Anstieg bis ca. $4.74\cdot 10^4$ ($f$ ca. $20$ MHz), Integralwert ca. $0.97\cdot 10^6$.
(16) Nur roter Parametersatz, $l=1$ km, $B=30$ MHz, $r=0.5$, Einstellung „Zweidrahtleitung $0.4$ mm“:
Anstieg bis ca. $3\cdot 10^8$ ($f$ ca. $23$ MHz), Integralwert ca. $4.55\cdot 10^9$; ohne $k_1$: $0.93\cdot 10^8$ ($f$ ca. $23$ MHz) bzw. $1.41\cdot 10^9$.
Quellenverzeichnis
- ↑ 1.0 1.1 Wellhausen, H. W.: Dämpfung, Phase und Laufzeiten bei Weitverkehrs–Koaxialpaaren. Frequenz 31, S. 23-28, 1977.
- ↑ 2.0 2.1 Pollakowski, M.; Wellhausen, H.W.: Eigenschaften symmetrischer Ortsanschlusskabel im Frequenzbereich bis 30 MHz. Mitteilung aus dem Forschungs- und Technologiezentrum der Deutschen Telekom AG, Darmstadt, Verlag für Wissenschaft und Leben Georg Heidecker, 1995.