Aufgaben:Exercise 3.7Z: Partial Fraction Decomposition

• Return to book

Einige Pol–Nullstellen–Konfigurationen

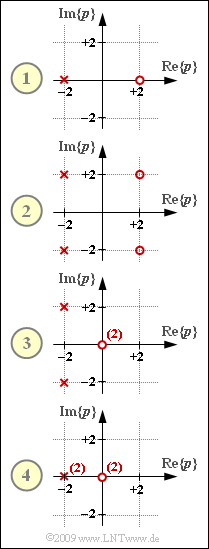
In der Grafik sind vier Vierpole durch ihre Pol–Nullstellen–Diagramme $H_{\rm L}(p)$ gegeben. Sie alle haben gemein, dass die Anzahl $Z$ der Nullstellen gleich der Anzahl $N$ der Polstellen ist. Der konstante Faktor ist jeweils $K=1$.

Im Sonderfall $Z = N$ kann zur Berechnung der Impulsantwort $h(t)$ der Residuensatz nicht direkt angewendet werden. Vielmehr muss vorher eine Partialbruchzerlegung entsprechend

$$H_{\rm L}(p) =1- H_{\rm L}\hspace{0.05cm}'(p) \hspace{0.05cm}$$

vorgenommen werden. Für die Impulsantwort gilt dann

$$h(t) = \delta(t)- h\hspace{0.03cm}'(t) \hspace{0.05cm},$$

wobei $h\hspace{0.03cm}'(t)$ die Laplace–Rücktransformierte von $H_{\rm L}\hspace{0.05cm}'(p)$ angibt, bei der die Bedingung $Z' < N'$ erfüllt ist.

Bei zwei der vier angegebenen Konfigurationen handelt es sich um so genannte Allpässe.

• Darunter versteht man Vierpole, bei denen die Fourier–Spektralfunktion die Bedingung $|H(f)| = 1$   ⇒ $a(f) = 0$ erfüllt.
• In der Aufgabe 3.4Z ist angegeben, wie die Pole und Nullstelle eines solchen Allpasses angeordnet sein müssen.

Weiterhin soll in dieser Aufgabe die $p$–Übertragungsfunktion

$$H_{\rm L}^{(5)}(p) =\frac{p/A}{\left (\sqrt{p/A}+\sqrt{A/p} \right )^2} \hspace{0.05cm}$$

⇒   „Konfiguration $(5)$” näher untersucht werden, die bei richtiger Wahl des Parameters $A$ durch eines der vier in der Grafik vorgegebenen Pol–Nullstellen–Diagramme dargestellt werden kann.

Hinweise:

• Die Aufgabe gehört zum Kapitel Laplace–Rücktransformation.
• Bezug genommen wird insbesondere auf die Seite Partialbruchzerlegung.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Bei welchen der skizzierten Vierpole handelt es sich um Allpässe?

	Konfiguration $(1)$,
	Konfiguration $(2)$,
	Konfiguration $(3)$,
	Konfiguration $(4)$.

2

Welcher Vierpol hat die Übertragungsfunktion $H_{\rm L}^{(5)}(p)$?

	Konfiguration $(1)$,
	Konfiguration $(2)$,
	Konfiguration $(3)$,
	Konfiguration $(4)$.

3

Berechnen Sie die Funktion $H_{\rm L}\hspace{0.01cm}'(p)$ nach einer Partialbruchzerlegung für die Konfiguration (1). Geben Sie den Funktionswert für $p = 0$ ein.

$H_{\rm L}\hspace{0.01cm}'(p = 0) \ = \ $

4

Berechnen Sie $H_{\rm L}\hspace{0.01cm}'(p)$ für Konfiguration $(2)$. Welche Aussagen treffen hier zu?

	$H_{\rm L}\hspace{0.01cm}'(p)$ besitzt die gleichen Nullstellen wie $H_{\rm L}(p)$.
	$H_{\rm L}\hspace{0.01cm}'(p)$ besitzt die gleichen Polstellen wie $H_{\rm L}(p)$.
	Der konstante Faktor von $H_{\rm L}\hspace{0.01cm}'(p)$ ist $K' = 8$.

5

Berechnen Sie $H_{\rm L}\hspace{0.01cm}'(p)$ für Konfiguration $(3)$. Welche Aussagen treffen hier zu?

	$H_{\rm L}\hspace{0.01cm}'(p)$ besitzt die gleichen Nullstellen wie $H_{\rm L}(p)$.
	$H_{\rm L}\hspace{0.01cm}'(p)$ besitzt die gleichen Polstellen wie $H_{\rm L}(p)$.
	Der konstante Faktor von $H_{\rm L}\hspace{0.01cm}'(p)$ ist $K' = 8$.

6

Berechnen Sie $H_{\rm L}\hspace{0.01cm}'(p)$ für Konfiguration $(4)$. Welche Aussagen treffen hier zu?

	$H_{\rm L}\hspace{0.01cm}'(p)$ besitzt die gleichen Nullstellen wie $H_{\rm L}(p)$.
	$H_{\rm L}\hspace{0.01cm}'(p)$ besitzt die gleichen Polstellen wie $H_{\rm L}(p)$.
	Der konstante Faktor von $H_{\rm L}\hspace{0.01cm}'(p)$ ist $K' = 8$.

Musterlösung

Solution

(1)  Nach den in der Zusatzaufgabe 3.4Z angegebenen Kriterien liegt immer dann ein Allpass vor, wenn es zu jeder Polstelle $p_{\rm x} = - A + {\rm j} \cdot B$ in der linken $p$–Halbebene eine entsprechende Nullstelle $p_{\rm o} = + A + {\rm j} \cdot B$ in der rechten Halbebene gibt. $K = 1$ ist dann die Dämpfungsfunktion $a(f) = 0 \ \rm Np$   ⇒   $|H(f)| = 1$. Aus der Grafik auf der Angabenseite erkennt man, dass die beiden Konfigurationen (1) und (2) genau diese Symmetrieeigenschaften aufweisen.

(2)  Die Übertragungsfunktion $H_{\rm L}^{(5)}(p)$ wird ebenso durch die Konfiguration (4) beschrieben, wie die nachfolgende Rechnung zeigt: $$H_{\rm L}^{(5)}(p) \hspace{0.25cm} = \hspace{0.2cm} \frac{p/A}{(\sqrt{p/A}+\sqrt{A/p})^2} =\frac{p/A}{{p/A}+2+ {A/p}} = \hspace{0.2cm}\frac{p^2}{p^2 + 2A \cdot p + A^2} = \frac{p^2}{(p+A)^2 }= H_{\rm L}^{(4)}(p) \hspace{0.05cm}.$$ Die doppelte Nullstelle liegt bei $p_{\rm o} = 0$, der doppelte Pol bei $p_{\rm x} = -A = -2$.

(3)  Für die Konfiguration (1) gilt: $$H_{\rm L}(p) =\frac{p-2}{p+2}=\frac{p+2-4}{p+2}= 1 - \frac{4}{p+2}=1- H_{\rm L}\hspace{-0.05cm}'(p) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}H_{\rm L}\hspace{-0.05cm}'(p) = \frac{4}{p+2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\hspace{0.15cm}\underline{H_{\rm L}\hspace{-0.05cm}'(p =0) =2} \hspace{0.05cm}.$$

(4)  In gleicher Weise ergibt sich für die Konfiguration (2): $$H_{\rm L}(p) =\frac{(p-2 - {\rm j} \cdot 2)(p-2 + {\rm j} \cdot 2)}{(p+2 - {\rm j} \cdot 2)(p+2 + {\rm j} \cdot 2)}= \frac{p^2 -4\cdot p +8 }{p^2 +4\cdot p +8}= \hspace{0.2cm}\frac{p^2 +4\cdot p +8 -8\cdot p}{p^2 +4\cdot p +8} $$ $$H_{\rm L}(p) =1- \frac{8\cdot p}{p^2 +4\cdot p +8}=1- H_{\rm L}\hspace{-0.05cm}'(p) \hspace{0.3cm}\Rightarrow \hspace{0.3cm}H_{\rm L}\hspace{0.05cm}'(p) = 8 \cdot \frac{p}{(p+2 - {\rm j} \cdot 2)(p+2 + {\rm j} \cdot 2)} \hspace{0.05cm}.$$ Richtig sind die beiden letzten Lösungsvorschläge im Gegensatz zur Aussage 1:

• Während $H_{\rm L}(p)$ zwei konjugiert–komplexe Nullstellen aufweist,
• besitzt $H_{\rm L}'(p)$ nur eine einzige Nullstelle bei $p_{\rm o}' = 0$.

(5)  Für die Konfiguration (3) gilt: $$H_{\rm L}(p) = \frac{p^2 }{p^2 +4\cdot p +8}=\frac{p^2 +4\cdot p +8 -4\cdot p -8 }{p^2 +4\cdot p +8} = 1- H_{\rm L}\hspace{-0.05cm}'(p)$$ $$\Rightarrow \hspace{0.3cm}H_{\rm L}\hspace{-0.05cm}'(p) = 4 \cdot \frac{p+2}{(p+2 - {\rm j} \cdot 2)(p+2 + {\rm j} \cdot 2)} \hspace{0.05cm}.$$ Die Nullstelle von $H_{\rm L}'(p)$ liegt nun bei $p_{\rm o}' = -2$ . Die Konstante ist $K' = 4$   ⇒   richtig ist hier nur die Aussage 2.

(6)  Schließlich gilt für die Konfiguration (4): $$H_{\rm L}(p) = \frac{p^2 }{(p+2)^2}=\frac{p^2 +4\cdot p +4 -4\cdot p -4 }{p^2 +4\cdot p +4} = 1- \frac{4\cdot p +4 }{p^2 +4\cdot p +4} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}H_{\rm L}\hspace{0.05cm}'(p) = 4 \cdot \frac{p+1}{(p+2)^2} \hspace{0.05cm}.$$ Richtig ist auch hier der Lösungsvorschlag 2. Allgemein lässt sich sagen:

• Durch die Partialbruchzerlegung wird die Anzahl und die Lage der Nullstellen verändert.
• Die Pole von $H_{\rm L}'(p)$ sind dagegen stets identisch mit denen von $H_{\rm L}(p)$.