Aufgaben:Exercise 1.2Z: Puls Code Modulation

• Return to book

Komponenten der Pulscodemodulation

Alle modernen Nachrichtenübertragungssysteme sind digital. Das Prinzip der digitalen Übertragung von Sprachsignalen geht auf Alec Reeves zurück, der die sogenannte Pulscodemodulation (PCM) bereits 1938 erfunden hat.

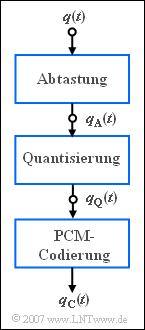
Rechts sehen Sie das (vereinfachte) Blockschaltbild des PCM-Senders mit drei Funktionseinheiten:

• Das bandbegrenzte Sprachsignal ${q(t)}$ wird abgetastet, wobei das Abtasttheorem zu beachten ist, und ergibt das abgetastete Signal $q_{\rm A}(t)$.
• Jeder Abtastwert $q_{\rm A}(t)$ wird auf einen von $M = 2^N$ quantisierten Werten abgebildet und führt zum quantisierten Signal $q_{\rm Q}(t)$.
• Jeder einzelne Quantisierungswert wird durch eine Codefolge von $N$ Binärsymbolen dargestellt und ergibt das codierte Signal $q_{\rm C}(t)$.

In dieser Aufgabe sollen nur die verschiedenen Signale des PCM-Senders klassifiziert werden. Spätere Aufgaben behandeln weitere Eigenschaften der Pulscodemodulation.

Hinweis:   Die Aufgabe gehört zum Kapitel Klassifizierung von Signalen.

Fragebogen

1

Welche der Aussagen sind für das Quellensignal ${q(t)}$ zutreffend?

	Im Normalbetrieb ist ${q(t)}$ ein stochastisches Signal.
	Ein deterministisches Quellensignal ist nur bei Testbetrieb oder für theoretische Untersuchungen sinnvoll.
	${q(t)}$ ist ein zeitdiskretes Signal.
	${q(t)}$ ist ein wertkontinuierliches Signal.

2

Welche der Aussagen treffen für das abgetastete Signal $q_{\rm A}(t)$ zu?

	$q_{\rm A}(t)$ ist ein wertdiskretes Signal.
	$q_{\rm A}(t)$ ist ein zeitdiskretes Signal.
	Je größer die maximale Frequenz des Nachrichtensignals ist, desto größer muss die Abtastrate gewählt werden.

3

Welche Aussagen sind für das quantisierte Signal $q_{\rm Q}(t)$ zutreffend, wenn $N = 8$ zugrunde gelegt wird?

	$q_{\rm Q}(t)$ ist ein zeitdiskretes Signal.
	$q_{\rm Q}(t)$ ist wertdiskret mit $M = 8$ möglichen Werten.
	$q_{\rm Q}(t)$ ist wertdiskret mit $M = 256$ möglichen Werten.
	$q_{\rm Q}(t)$ ist ein Binärsignal.

4

Welche Aussagen sind für das codierte Signal $q_{\rm C}(t)$ zutreffend, wenn $N = 8$ zugrunde gelegt wird?

	$q_{\rm C}(t)$ ist ein zeitdiskretes Signal.
	$q_{\rm C}(t)$ ist ein wertdiskretes Signal mit $M = 8$ möglichen Werten.
	$q_{\rm C}(t)$ ist ein Binärsignal.
	Bei Abtastung im Abstand $T_{\rm A}$ beträgt die Bitdauer $T_{\rm B} = T_{\rm A}$.
	Bei Abtastung im Abstand $T_{\rm A}$ beträgt die Bitdauer $T_{\rm B} = T_{\rm A}/8$.

Musterlösung

Solution

(1)  Richtig sind die Lösungsvorschläge 1, 2 und 4:

• Das Quellensignal ${q(t)}$ ist analog, also wert- und zeitkontinuierlich.
• Im Allgemeinen macht es keinen Sinn, ein deterministisches Signal zu übertragen.
• Für die mathematische Beschreibung eignet sich allerdings ein deterministisches Quellensignal – wie zum Beispiel ein periodisches Signal – besser als ein Zufallssignal.
• Deterministische Signale werden auch für den Testbetrieb herangezogen, um erkannte Fehlfunktionen rekonstruieren zu können.

(2)  Richtig sind die Lösungsvorschläge 2 und 3:

• Das Signal $q_{\rm A}(t)$ nach der Abtastung ist weiterhin wertkontinuierlich, aber nun zeitdiskret.
• Die Abtastfrequenz $f_{\rm A}$ ist dabei durch das so genannte Abtasttheorem vorgegeben.
• Je größer die maximale Frequenz $f_{\rm N,\,max}$ des Nachrichtensignals ist, desto größer muss $f_{\rm A} ≥ 2 \cdot f_{\rm N,\,max}$ gewählt werden.

(3)  Richtig sind die Lösungsvorschläge 1 und 3:

• Das quantisierte Signal $q_{\rm A}(t)$ ist zeit- und wertdiskret, wobei die Stufenzahl $M = 2^8 = 256$ beträgt.
• Ein Binärsignal ist dagegen ein wertdiskretes Signal mit der Stufenzahl $M = 2$.

(4)  Das codierte Signal $q_{\rm C}(t)$ ist binär (Stufenzahl $M = 2$) mit Bitdauer $T_{\rm B} = T_{\rm A}/8$. Richtig sind hier die Lösungsvorschläge 1, 3 und 5.