Difference between revisions of "Aufgaben:Exercise 2.3Z: Oscillation Parameters"
From LNTwww
m (Textersetzung - „*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.“ durch „ “) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
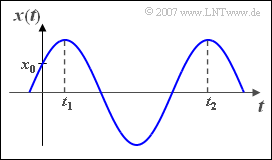
| − | [[File:P_ID316__Sig_Z_2_3.png|right|frame| | + | [[File:P_ID316__Sig_Z_2_3.png|right|frame|Definition von $x-0$, $t_1$ und $t_2$]] |
Jede harmonische Schwingung kann auch in der Form | Jede harmonische Schwingung kann auch in der Form | ||
:$$x(t)=C\cdot\cos\bigg(2\pi \cdot \frac{t-\tau}{T_0}\bigg)$$ | :$$x(t)=C\cdot\cos\bigg(2\pi \cdot \frac{t-\tau}{T_0}\bigg)$$ | ||
| Line 13: | Line 13: | ||
:* die Verschiebung $\tau$ gegenüber einem Cosinussignal. | :* die Verschiebung $\tau$ gegenüber einem Cosinussignal. | ||
| + | |||
Eine zweite Darstellungsform lautet mit der Grundfrequenz $f_0$ und der Phase $\varphi$: | Eine zweite Darstellungsform lautet mit der Grundfrequenz $f_0$ und der Phase $\varphi$: | ||
| Line 27: | Line 28: | ||
| − | '' | + | ''Hinweis:'' |
*Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Harmonische_Schwingung|Harmonische Schwingung]]. | *Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Harmonische_Schwingung|Harmonische Schwingung]]. | ||
| Line 55: | Line 56: | ||
{Wie lautet das Spektrum $X(f)$? Welches Gewicht hat die Spektrallinie bei $+f_0$? | {Wie lautet das Spektrum $X(f)$? Welches Gewicht hat die Spektrallinie bei $+f_0$? | ||
|type="{}"} | |type="{}"} | ||
| − | $\text{Re}[X(f = f_0)]\ = \ $ { 1.5 3% } $\text{V}$ | + | $\text{Re}\big[X(f = f_0)\big]\ = \ $ { 1.5 3% } $\text{V}$ |
| − | $\text{Im}[X(f = f_0)] \ = \ $ { -2.65--2.55 } $\text{V}$ | + | $\text{Im}\big[X(f = f_0)\big] \ = \ $ { -2.65--2.55 } $\text{V}$ |
| Line 64: | Line 65: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Es gilt $T_0 = t_2 | + | '''(1)''' Es gilt $T_0 = t_2 - t_1 = 12\, \text{ms}$ und $f_0 = 1/T_0 \hspace{0.15cm} \underline{\approx 83.33\, \text{Hz}}$. |
| − | '''(2)''' Die Verschiebung beträgt $\tau = 2\, \text{ms}$ und die Phase ist $\varphi = 2\pi \cdot \tau/T_0 = \pi/3$ entsprechend $60^{\circ}$. | + | '''(2)''' Die Verschiebung beträgt $\tau \hspace{0.1cm} \underline{= 2\, \text{ms}}$ und die Phase ist $\varphi = 2\pi \cdot \tau/T_0 = \pi/3$ entsprechend $\varphi =\hspace{0.15cm} \underline{60^{\circ}}$. |
| − | '''(3)''' Aus dem Wert zum Zeitpunkt $t = 0$ folgt für die Amplitude ${C | + | '''(3)''' Aus dem Wert zum Zeitpunkt $t = 0$ folgt für die Amplitude ${C}$: |
:$$x_0=x(t=0)=C\cdot\cos(-60\,^\circ)={C}/{2}=\rm 3\,V | :$$x_0=x(t=0)=C\cdot\cos(-60\,^\circ)={C}/{2}=\rm 3\,V | ||
\hspace{0.3 cm} \Rightarrow \hspace{0.3 cm}\hspace{0.15cm}\underline{\it C=\rm 6\,V}.$$ | \hspace{0.3 cm} \Rightarrow \hspace{0.3 cm}\hspace{0.15cm}\underline{\it C=\rm 6\,V}.$$ | ||
| Line 77: | Line 78: | ||
:$$X(f)={C}/{2}\cdot{\rm e}^{-{\rm j}\varphi}\cdot\delta(f-f_0)+{C}/{2}\cdot{\rm e}^{{\rm j}\varphi}\cdot\delta(f+f_0).$$ | :$$X(f)={C}/{2}\cdot{\rm e}^{-{\rm j}\varphi}\cdot\delta(f-f_0)+{C}/{2}\cdot{\rm e}^{{\rm j}\varphi}\cdot\delta(f+f_0).$$ | ||
| − | :Das Gewicht der Diraclinie bei $f = f_0$ (erster Term) ist ${C}/2 \cdot {\rm e}^{–\text{j}\varphi} \hspace{0.05cm}\approx \underline{1.5 \,\text{V} - \text{j} \cdot 2.6 \,\text{V}}$. | + | :Das Gewicht der Diraclinie bei $f = f_0$ (erster Term) ist ${C}/2 \cdot {\rm e}^{–\text{j}\varphi} = 3 \,\text{V} \cdot \cos(60^\circ)- 3 \,\text{V} \cdot \sin(60^\circ)\hspace{0.05cm}\approx \underline{1.5 \,\text{V} - \text{j} \cdot 2.6 \,\text{V}}$. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
[[Category:Aufgaben zu Signaldarstellung|^2. Periodische Signale^]] | [[Category:Aufgaben zu Signaldarstellung|^2. Periodische Signale^]] | ||
Revision as of 14:37, 12 July 2018
Jede harmonische Schwingung kann auch in der Form
- $$x(t)=C\cdot\cos\bigg(2\pi \cdot \frac{t-\tau}{T_0}\bigg)$$
geschrieben werden. Die Schwingung ist somit durch drei Parameter vollständig bestimmt:
- die Amplitude $C$,
- die Periodendauer $T_0$,
- die Verschiebung $\tau$ gegenüber einem Cosinussignal.
Eine zweite Darstellungsform lautet mit der Grundfrequenz $f_0$ und der Phase $\varphi$:
- $$x(t)=C \cdot\cos(2\pi f_0t-\varphi).$$
Von einer harmonischen Schwingung ist nun bekannt, dass
- das erste Signalmaximum bei $t_1 = 2 \,\text{ms}$ auftritt,
- das zweite Signalmaximum bei $t_2 = 14 \,\text{ms}$ auftritt,
- der Wert $x_0 ={x(t = 0)} = 3 \,\text{V}$ ist.
Hinweis:
- Die Aufgabe gehört zum Kapitel Harmonische Schwingung.
Fragebogen
Musterlösung
(1) Es gilt $T_0 = t_2 - t_1 = 12\, \text{ms}$ und $f_0 = 1/T_0 \hspace{0.15cm} \underline{\approx 83.33\, \text{Hz}}$.
(2) Die Verschiebung beträgt $\tau \hspace{0.1cm} \underline{= 2\, \text{ms}}$ und die Phase ist $\varphi = 2\pi \cdot \tau/T_0 = \pi/3$ entsprechend $\varphi =\hspace{0.15cm} \underline{60^{\circ}}$.
(3) Aus dem Wert zum Zeitpunkt $t = 0$ folgt für die Amplitude ${C}$:
- $$x_0=x(t=0)=C\cdot\cos(-60\,^\circ)={C}/{2}=\rm 3\,V \hspace{0.3 cm} \Rightarrow \hspace{0.3 cm}\hspace{0.15cm}\underline{\it C=\rm 6\,V}.$$
(4) Die dazugehörige Spektralfunktion lautet:
- $$X(f)={C}/{2}\cdot{\rm e}^{-{\rm j}\varphi}\cdot\delta(f-f_0)+{C}/{2}\cdot{\rm e}^{{\rm j}\varphi}\cdot\delta(f+f_0).$$
- Das Gewicht der Diraclinie bei $f = f_0$ (erster Term) ist ${C}/2 \cdot {\rm e}^{–\text{j}\varphi} = 3 \,\text{V} \cdot \cos(60^\circ)- 3 \,\text{V} \cdot \sin(60^\circ)\hspace{0.05cm}\approx \underline{1.5 \,\text{V} - \text{j} \cdot 2.6 \,\text{V}}$.