Difference between revisions of "Applets:Physikalisches Signal & Äquivalentes TP-Signal"
| Line 68: | Line 68: | ||
| − | Aufgrund der Unsymmetrie von $X_+(f)$ bezüglich der Frequenz $f = 0$ kann man bereits jetzt schon sagen, dass die Zeitfunktion $x_+(t)$ bis auf einen trivialen Sonderfall $x_+(t)= 0 \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\ X_+(f)= 0$ stets komplex ist. | + | Aufgrund der Unsymmetrie von $X_+(f)$ bezüglich der Frequenz $f = 0$ kann man bereits jetzt schon sagen, dass die Zeitfunktion $x_+(t)$ bis auf einen trivialen Sonderfall $x_+(t)= 0 \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\ \ X_+(f)= 0$ stets komplex ist. |
| Line 78: | Line 78: | ||
Man erkennt, dass $x_{\rm TP}(t)$ im Allgemeinen komplexwertig ist. Ist aber $X_+(f)$ symmetrisch um die Trägerfrequenz $f_{\rm T}$, so ist $X_{\rm TP}(f)$ symmetrisch um die Frequenz $f=0$ und es ergibt sich dementsprechend eine reelle Zeitfunktion $x_{\rm TP}(t)$. | Man erkennt, dass $x_{\rm TP}(t)$ im Allgemeinen komplexwertig ist. Ist aber $X_+(f)$ symmetrisch um die Trägerfrequenz $f_{\rm T}$, so ist $X_{\rm TP}(f)$ symmetrisch um die Frequenz $f=0$ und es ergibt sich dementsprechend eine reelle Zeitfunktion $x_{\rm TP}(t)$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ===$x_ | + | ===$x_{\rm TP}(t)$–Darstellung einer Summe aus drei harmonischen Schwingungen=== |
In unserem Applet setzen wir stets einen Zeigerverbund aus drei Drehzeigern voraus. Das physikalische Signal lautet: | In unserem Applet setzen wir stets einen Zeigerverbund aus drei Drehzeigern voraus. Das physikalische Signal lautet: | ||
| Line 105: | Line 88: | ||
*Die Indizes sind an das Modulationsverfahren [[Modulationsverfahren/Zweiseitenband-Amplitudenmodulation|Zweiseitenband–Amplitudenmodulation]] angelehnt. „T” steht für „Träger”, „U” für „Unteres Seitenband” und „O” für „Oberes Seitenband”. Entsprechend gilt stets $f_{\rm U} < f_{\rm T}$ und $f_{\rm O} > f_{\rm T}$. Für die Amplituden und Phasen gibt es keine Einschränkungen. | *Die Indizes sind an das Modulationsverfahren [[Modulationsverfahren/Zweiseitenband-Amplitudenmodulation|Zweiseitenband–Amplitudenmodulation]] angelehnt. „T” steht für „Träger”, „U” für „Unteres Seitenband” und „O” für „Oberes Seitenband”. Entsprechend gilt stets $f_{\rm U} < f_{\rm T}$ und $f_{\rm O} > f_{\rm T}$. Für die Amplituden und Phasen gibt es keine Einschränkungen. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Das dazugehörige äquivalente Tiefpass–Signal lautet mit $f_{\rm O}\hspace{0.01cm}' = f_{\rm O}- f_{\rm T} > 0$, $f_{\rm U}\hspace{0.01cm}' = f_{\rm U}- f_{\rm T} < 0$ und $f_{\rm T}\hspace{0.01cm}' = 0$: | ||
| + | |||
| + | :$$x_{\rm TP}(t) = x_\text{TP, T}(t) + x_\text{TP, O}(t) + x_\text{TP, U}(t) = A_{\rm T}\cdot {\rm e}^{-{\rm j} \varphi_{\rm T} } \hspace{0.1cm}+ \hspace{0.1cm} A_{\rm O}\cdot {\rm e}^{-{\rm j} \varphi_{\rm O} } \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm O}\hspace{0.01cm}'\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm}+ \hspace{0.1cm} | ||
| + | A_{\rm U}\cdot {\rm e}^{-{\rm j} \varphi_{\rm U} } \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm U}\hspace{0.01cm}'\hspace{0.05cm}\cdot \hspace{0.05cm}t} . $$ | ||
| + | |||
| + | '''Bild und Text von Beispiel 1 ändern''' | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel | + | $\text{Beispiel 1:}$ |
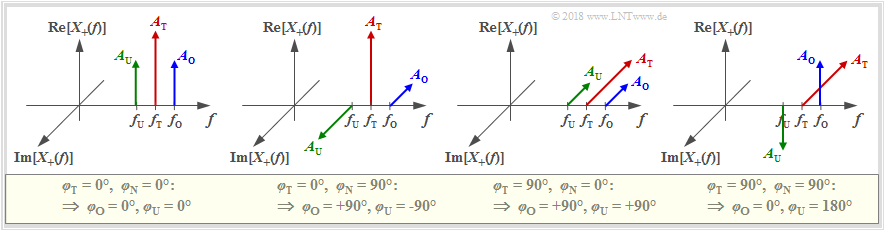
Die hier angegebene Konstellation ergibt sich zum Beispiel bei der [[Modulationsverfahren/Zweiseitenband-Amplitudenmodulation#AM-Signale_und_-Spektren_bei_harmonischem_Eingangssignal|Zweiseitenband-Amplitudenmodulation]] des Nachrichtensignals $x_{\rm N}(t) = A_{\rm N}\cdot \cos\left(2\pi f_{\rm N}\cdot t- \varphi_{\rm N}\right)$ mit dem Trägersignal $x_{\rm T}(t) = A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t - \varphi_{\rm T}\right)$. Hierauf wird in der Versuchsdurchführung häufiger eingegangen. | Die hier angegebene Konstellation ergibt sich zum Beispiel bei der [[Modulationsverfahren/Zweiseitenband-Amplitudenmodulation#AM-Signale_und_-Spektren_bei_harmonischem_Eingangssignal|Zweiseitenband-Amplitudenmodulation]] des Nachrichtensignals $x_{\rm N}(t) = A_{\rm N}\cdot \cos\left(2\pi f_{\rm N}\cdot t- \varphi_{\rm N}\right)$ mit dem Trägersignal $x_{\rm T}(t) = A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t - \varphi_{\rm T}\right)$. Hierauf wird in der Versuchsdurchführung häufiger eingegangen. | ||
| Line 122: | Line 107: | ||
[[File:Zeigerdiagramm_2_neu.png|center|frame|Spektum $X_+(f)$ des analytischen Signals für verschiedene Phasenkonstellationen |class=fit]]}} | [[File:Zeigerdiagramm_2_neu.png|center|frame|Spektum $X_+(f)$ des analytischen Signals für verschiedene Phasenkonstellationen |class=fit]]}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ===Darstellung des äquivalenten TP–Signals nach Betrag und Phase=== | |
| − | |||
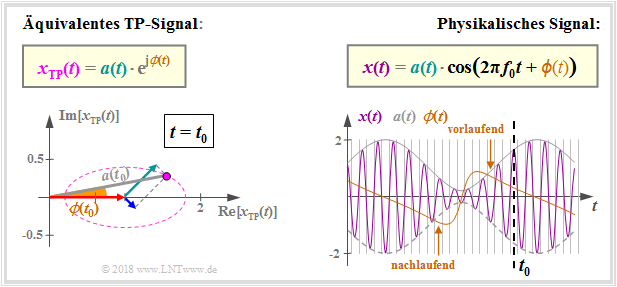
| + | Das im Allgemeinen komplexwertige äquivalenten TP–Signal | ||
| + | :$$x_{\rm TP}(t) = a(t) \cdot {\rm e}^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \phi(t) }$$ | ||
| + | kann entsprechend der hier angegebenen Gleichung in eine Betragsfunktion $a(t)$ und eine Phasenfunktion $\phi(t)$ aufgespalten werden, wobei gilt: | ||
| + | :$$a(t) = \vert x_{\rm TP}(t)\vert = \sqrt{ {\rm Re}^2\big [x_{\rm TP}(t)\big ] + {\rm Im}^2\big [x_{\rm TP}(t)\big ] }\hspace{0.05cm},$$ | ||
| + | :$$\phi(t) = \text{arc }x_{\rm TP}(t) = \arctan \frac{{\rm Im}\big [x_{\rm TP}(t)\big ]}{{\rm Re}\big [x_{\rm TP}(t)\big ]}.$$ | ||
| − | + | Der Grund dafür, dass man ein Bandpass–Signal $x(t)$ meist durch das äquivalente TP–Signal $x_{\rm TP}(t)$ beschreibt ist, dass die Funktionen $a(t)$ und $\phi(t)$ in beiden Darstellungen interpretierbar sind: | |
| − | + | *Der Betrag $a(t)$ des äquivalentes TP–Signals $x_{\rm TP}(t)$ gibt die (zeitabhängige) Hüllkurve von $x(t)$ an. | |
| − | + | *Die Phase $\phi(t)$ von $x_{\rm TP}(t)$ kennzeichnet die Lage der Nulldurchgänge von $x(t)$, wobei gilt: | |
| − | + | :– Bei $\phi(t)>0$ ist der Nulldurchgang früher als seine Solllage ⇒ das Signal ist hier vorlaufend. | |
| − | + | :– Bei $\phi(t)<0$ ist der Nulldurchgang später als seine Solllage ⇒ das Signal ist hier nachlaufend. | |
| − | *$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 2:}$ | + | $\text{Beispiel 2:}$ |
| + | Die Grafik soll diesen Zusammenhang verdeutlichen, wobei $A_{\rm U} > A_{\rm O}$ vorausgesetzt ist ⇒ der grüne Zeiger (für das untere Seitenband) ist länger als der blaue Zeiger (oberes Seitenband). Es handelt sich um eine Momentaufnahme zum Zeitpunkt $t_0$: | ||
| − | [[File: | + | [[File:Ortskurve_3_neu.png|center|frame|Bandpass–Spektrum $X(f)$ |class=fit]] |
| − | + | *Bei diesen Systemparametern liegt die Spitze des Zeigerverbundes $x_{\rm TP}(t)$ – also die geometrisch Summe aus rotem, blauem und grünem Zeiger – auf einer Ellipse. | |
| − | * | + | * In der linken Grafik schwarz eingezeichnet ist der Betrag $a(t_0) = \vert x_{\rm TP}(t_0) \vert$ und in brauner Farbe angedeutet ist der Phasenwert $\phi(t_0) = \text{arc }x_{\rm TP}(t_0) > 0.$ |
| − | * | + | *In der rechten Grafik gibt der Betrag $a(t_0) = \vert x_{\rm TP}(t_0) \vert$ des äquivalenten TP–Signals die Hüllkurve des physikalischen Signals $x(t)$ an. |
| − | + | * Bei $\phi(t) \equiv 0$ würden alle Nulldurchgänge von $x(t)$ in äquidistenten Abständen auftreten. Wegen $\phi(t_0) > 0$ ist zum Zeitpunkt $t_0$ das Signal vorlaufend, das heißt: Die Nulldurchgänge kommen früher, als es das Raster vorgibt. }} | |
| − | * | ||
| − | |||
Revision as of 12:49, 30 July 2018
Contents
Programmbeschreibung
Dieses Applet zeigt den Zusammenhang zwischen dem physikalischen Bandpass–Signal $x(t)$ und dem dazugehörigen äquivalenten Tiefpass–Signal $x_{\rm TP}(t)$. Ausgegangen wird stets von einem Bandpass–Signal $x(t)$ mit frequenzdiskretem Spektrum $X(f)$:
- $$x(t) = x_{\rm T}(t) + x_{\rm O}(t) + x_{\rm U}(t) = A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t- \varphi_{\rm T}\right)+A_{\rm O}\cdot \cos\left(2\pi f_{\rm O}\cdot t- \varphi_{\rm O}\right)+ A_{\rm U}\cdot \cos\left(2\pi f_{\rm U}\cdot t- \varphi_{\rm U}\right). $$
Das physikalische Signal $x(t)$ setzt sich also aus drei harmonischen Schwingungen zusammen, einer Konstellation, die sich zum Beispiel bei der Zweiseitenband-Amplitudenmodulation des Nachrichtensignals $x_{\rm N}(t) = A_{\rm N}\cdot \cos\left(2\pi f_{\rm N}\cdot t- \varphi_{\rm N}\right)$ mit dem Trägersignal $x_{\rm T}(t) = A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t - \varphi_{\rm T}\right)$ ergibt. Die Nomenklatur ist ebenfalls an diesen Fall angepasst:
- $x_{\rm O}(t)$ bezeichnet das „Obere Seitenband” mit der Amplitude $A_{\rm O}= A_{\rm N}/2$, der Frequenz $f_{\rm O} = f_{\rm T} + f_{\rm N}$ und der Phase $\varphi_{\rm O} = \varphi_{\rm T} + \varphi_{\rm N}$.
- Entsprechend gilt für das „Untere Seitenband” $x_{\rm U}(t)$ mit $f_{\rm U} = f_{\rm T} - f_{\rm N}$, $A_{\rm U}= A_{\rm O}$ und $\varphi_{\rm U} = -\varphi_{\rm O}$.
Das dazugehörige äquivalente Tiefpass–Signal lautet mit $f_{\rm O}\hspace{0.01cm}' = f_{\rm O}- f_{\rm T} > 0$, $f_{\rm U}\hspace{0.01cm}' = f_{\rm U}- f_{\rm T} < 0$ und $f_{\rm T}\hspace{0.01cm}' = 0$:
- $$x_{\rm TP}(t) = x_\text{TP, T}(t) + x_\text{TP, O}(t) + x_\text{TP, U}(t) = A_{\rm T}\cdot {\rm e}^{-{\rm j} \varphi_{\rm T} } \hspace{0.1cm}+ \hspace{0.1cm} A_{\rm O}\cdot {\rm e}^{-{\rm j} \varphi_{\rm O} } \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm O}\hspace{0.01cm}'\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm}+ \hspace{0.1cm} A_{\rm U}\cdot {\rm e}^{-{\rm j} \varphi_{\rm U} } \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm U}\hspace{0.01cm}'\hspace{0.05cm}\cdot \hspace{0.05cm}t} . $$
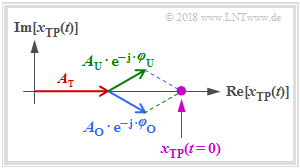
Im Programm dargestellt wird $x_{\rm TP}(t)$ als vektorielle Summe dreier Drehzeiger als violetter Punkt (siehe beispielhafte Grafik für den Startzeitpunkt $t=0$ und cosinusförmigem Träger):
- Der (rote) Zeiger des Trägers $x_\text{TP, T}(t)$ mit der Länge $A_{\rm T}$ und der Nullphasenlage $\varphi_{\rm T} = 0$ liegt in der komplexen Ebene fest. Es gilt also für alle Zeiten $t$: $x_{\rm TP}(t)= A_{\rm T}\cdot {\rm e}^{-{\rm j} \varphi_{\rm T} }$.
- Der (blaue) Zeiger des Oberen Seitenbandes $x_\text{TP, O}(t)$ mit der Länge $A_{\rm O}$ und der Nullphasenlage $\varphi_{\rm O}$ dreht mit der Winkelgeschwindigkeit $2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm O}\hspace{0.01cm}'$ in mathematisch positiver Richtung (eine Umdrehung in der Zeit $1/f_{\rm O}\hspace{0.01cm}')$.
- Der (grüne) Zeiger des Unteren Seitenbandes $x_{\rm U+}(t)$ mit der Länge $A_{\rm U}$ und der Nullphasenlage $\varphi_{\rm U}$ dreht mit der Winkelgeschwindigkeit $2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm U}\hspace{0.01cm}'$, wegen $f_{\rm U}\hspace{0.01cm}'<0$ im Uhrzeigersinn (mathematisch negative Richtung).
- Mit $f_{\rm U}\hspace{0.01cm}' = -f_{\rm O}\hspace{0.01cm}'$ drehen der blaue und der grüne Zeiger gleich schnell, aber in unterschiedlichen Richtungen. Gilt zudem $A_{\rm O} = A_{\rm U}$ und $\varphi_{\rm U} = -\varphi_{\rm O}$, so bewegt sich $x_{\rm TP}(t)$ auf einer Geraden mit einer Neigung von $\varphi_{\rm T}$.
Hinweis: Die Grafik gilt für $\varphi_{\rm O} = +30^\circ$. Daraus folgt für den Startzeitpunkt $t=0$ der Winkel des blauen Zeigers (OSB) gegenüber dem Koordinatensystem: $\phi_{\rm O} = -\varphi_{\rm O} = -30^\circ$. Ebenso folgt aus der Nullphanlage $\varphi_{\rm U} = -30^\circ$ des unteren Seitenbandes (USB, grüner Zeiger) für den in der komplexen Ebene zu berücksichtigenden Phasenwinkel: $\phi_{\rm U} = +30^\circ$.
Den zeitlichen Verlauf von $x_{\rm TP}(t)$ bezeichnen wir im Folgenden auch als Ortskurve. Der Zusammenhang zwischen $x_{\rm TP}(t)$ und dem physikalischen Bandpass–Signal $x(t)$ wird im Abschnitt ??? angegeben. Der Zusammenhang zwischen $x_{\rm TP}(t)$ und dem dazugehörigen analytischen Signal $x_+(t)$ lautet:
- $$x_{\rm TP}(t) = x_{\rm +}(t)\cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \cdot f_{\rm T}\cdot \hspace{0.05cm}t},$$
- $$x_{\rm +}(t) = x_{\rm TP}(t)\cdot {\rm e}^{+{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \cdot f_{\rm T}\cdot \hspace{0.05cm}t}.$$
Theoretischer Hintergrund
Beschreibungsmöglichkeiten von Bandpass-Signalen
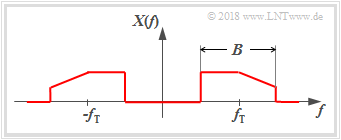
Wir betrachten hier Bandpass-Signale $x(t)$ mit der Eigenschaft, dass deren Spektren $X(f)$ nicht im Bereich um die Frequenz $f = 0$ liegen, sondern um eine Trägerfrequenz $f_{\rm T}$. Meist kann auch davon ausgegangen werden, dass die Bandbreite $B \ll f_{\rm T}$ ist.
Die Grafik zeigt ein solches Bandpass–Spektrum $X(f)$. Unter der Annahme, dass das zugehörige $x(t)$ ein physikalisches Signal und damit reell ist, ergibt sich für die Spektralfunktion $X(f)$ eine Symmetrie bezüglich der Frequenz $f = 0$. Ist $x(t)$ eine gerade Funktion ⇒ $x(-t)=x(+t)$, so ist auch $X(f)$ reell und gerade.
Neben dem physikalischen Signal $x(t)\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X(f)$ verwendet man zur Beschreibung von Bandpass-Signalen gleichermaßen:
- das analytische Signal $x_+(t)\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X_+(f)$, siehe Applet Physikalisches Signal & Analytisches Signal,
- das äquivalente Tiefpass–Signal $x_{\rm TP}(t)\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X_{\rm TP}(f)$, wie im nächsten Unterabschnitt beschrieben.
Spektralfunktionen des analytischen und des äquivalenten TP–Signals
Das zum physikalischen Signal $x(t)$ gehörige analytische Signal $x_+(t)$ ist diejenige Zeitfunktion, deren Spektrum folgende Eigenschaft erfüllt:
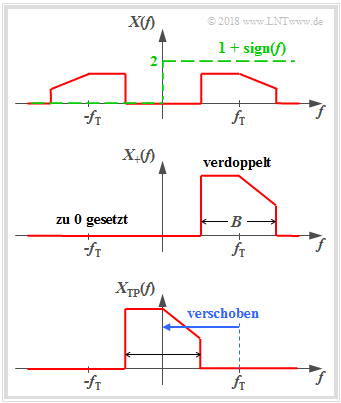
- $$X_+(f)=\big[1+{\rm sign}(f)\big] \cdot X(f) = \left\{ {2 \cdot X(f) \; \hspace{0.2cm}\rm f\ddot{u}r\hspace{0.2cm} {\it f} > 0, \atop {\,\,\,\, \rm 0 \; \hspace{0.9cm}\rm f\ddot{u}r\hspace{0.2cm} {\it f} < 0.} }\right.$$
Die so genannte Signumfunktion ist dabei für positive Werte von $f$ gleich $+1$ und für negative $f$–Werte gleich $-1$.
- Der (beidseitige) Grenzwert liefert $\sign(0) = 0$.
- Der Index „+” soll deutlich machen, dass $X_+(f)$ nur Anteile bei positiven Frequenzen besitzt.
Aus der Grafik erkennt man die Berechnungsvorschrift für $X_+(f)$: Das tatsächliche BP–Spektrum $X(f)$ wird
- bei den positiven Frequenzen verdoppelt, und
- bei den negativen Frequenzen zu Null gesetzt.
Aufgrund der Unsymmetrie von $X_+(f)$ bezüglich der Frequenz $f = 0$ kann man bereits jetzt schon sagen, dass die Zeitfunktion $x_+(t)$ bis auf einen trivialen Sonderfall $x_+(t)= 0 \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\ \ X_+(f)= 0$ stets komplex ist.
Zum Spektrum $X_{\rm TP}(f)$ des äquivalenten TP–Signals kommt man, indem man $X_+(f)$ um die Trägerfrequenz $f_{\rm T}$ nach links verschiebt:
- $$X_{\rm TP}(f)= X_+(f+f_{\rm T}).$$
Im Zeitbereich entspricht diese Operation der Multiplkation von $x_{\rm +}(t)$ mit der komplexen Exponentialfunktion mit negativem Exponenten:
- $$x_{\rm TP}(t) = x_{\rm +}(t)\cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \cdot f_{\rm T}\cdot \hspace{0.05cm}t}.$$
Man erkennt, dass $x_{\rm TP}(t)$ im Allgemeinen komplexwertig ist. Ist aber $X_+(f)$ symmetrisch um die Trägerfrequenz $f_{\rm T}$, so ist $X_{\rm TP}(f)$ symmetrisch um die Frequenz $f=0$ und es ergibt sich dementsprechend eine reelle Zeitfunktion $x_{\rm TP}(t)$.
$x_{\rm TP}(t)$–Darstellung einer Summe aus drei harmonischen Schwingungen
In unserem Applet setzen wir stets einen Zeigerverbund aus drei Drehzeigern voraus. Das physikalische Signal lautet:
- $$x(t) = x_{\rm U}(t) + x_{\rm T}(t) + x_{\rm O}(t) = A_{\rm U}\cdot \cos\left(2\pi f_{\rm U}\cdot t- \varphi_{\rm U}\right)+A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t- \varphi_{\rm T}\right)+A_{\rm O}\cdot \cos\left(2\pi f_{\rm O}\cdot t- \varphi_{\rm O}\right). $$
- Jede der drei harmonischen Schwingungen harmonischen Schwingungen $x_{\rm T}(t)$, $x_{\rm U}(t)$ und $x_{\rm O}(t)$ wird durch eine Amplitude $(A)$, eine Frequenz $(f)$ und einen Phasenwert $(\varphi)$ charakterisiert.
- Die Indizes sind an das Modulationsverfahren Zweiseitenband–Amplitudenmodulation angelehnt. „T” steht für „Träger”, „U” für „Unteres Seitenband” und „O” für „Oberes Seitenband”. Entsprechend gilt stets $f_{\rm U} < f_{\rm T}$ und $f_{\rm O} > f_{\rm T}$. Für die Amplituden und Phasen gibt es keine Einschränkungen.
Das dazugehörige äquivalente Tiefpass–Signal lautet mit $f_{\rm O}\hspace{0.01cm}' = f_{\rm O}- f_{\rm T} > 0$, $f_{\rm U}\hspace{0.01cm}' = f_{\rm U}- f_{\rm T} < 0$ und $f_{\rm T}\hspace{0.01cm}' = 0$:
- $$x_{\rm TP}(t) = x_\text{TP, T}(t) + x_\text{TP, O}(t) + x_\text{TP, U}(t) = A_{\rm T}\cdot {\rm e}^{-{\rm j} \varphi_{\rm T} } \hspace{0.1cm}+ \hspace{0.1cm} A_{\rm O}\cdot {\rm e}^{-{\rm j} \varphi_{\rm O} } \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm O}\hspace{0.01cm}'\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm}+ \hspace{0.1cm} A_{\rm U}\cdot {\rm e}^{-{\rm j} \varphi_{\rm U} } \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm U}\hspace{0.01cm}'\hspace{0.05cm}\cdot \hspace{0.05cm}t} . $$
Bild und Text von Beispiel 1 ändern
$\text{Beispiel 1:}$ Die hier angegebene Konstellation ergibt sich zum Beispiel bei der Zweiseitenband-Amplitudenmodulation des Nachrichtensignals $x_{\rm N}(t) = A_{\rm N}\cdot \cos\left(2\pi f_{\rm N}\cdot t- \varphi_{\rm N}\right)$ mit dem Trägersignal $x_{\rm T}(t) = A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t - \varphi_{\rm T}\right)$. Hierauf wird in der Versuchsdurchführung häufiger eingegangen.
Bei dieser Betrachtungsweise gibt es einige Einschränkungen bezüglich der Programmparameter:
- Für die Frequenzen gelte stets $f_{\rm O} = f_{\rm T} + f_{\rm N}$ und $f_{\rm U} = f_{\rm T} - f_{\rm N}$.
- Ohne Verzerrungen sind die Amplitude der Seitenbänder $A_{\rm O}= A_{\rm O}= A_{\rm N}/2$.
- Die jeweiligen Phasenverhältnisse können der nachfolgenden Grafik entnommen werden.
Darstellung des äquivalenten TP–Signals nach Betrag und Phase
Das im Allgemeinen komplexwertige äquivalenten TP–Signal
- $$x_{\rm TP}(t) = a(t) \cdot {\rm e}^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \phi(t) }$$
kann entsprechend der hier angegebenen Gleichung in eine Betragsfunktion $a(t)$ und eine Phasenfunktion $\phi(t)$ aufgespalten werden, wobei gilt:
- $$a(t) = \vert x_{\rm TP}(t)\vert = \sqrt{ {\rm Re}^2\big [x_{\rm TP}(t)\big ] + {\rm Im}^2\big [x_{\rm TP}(t)\big ] }\hspace{0.05cm},$$
- $$\phi(t) = \text{arc }x_{\rm TP}(t) = \arctan \frac{{\rm Im}\big [x_{\rm TP}(t)\big ]}{{\rm Re}\big [x_{\rm TP}(t)\big ]}.$$
Der Grund dafür, dass man ein Bandpass–Signal $x(t)$ meist durch das äquivalente TP–Signal $x_{\rm TP}(t)$ beschreibt ist, dass die Funktionen $a(t)$ und $\phi(t)$ in beiden Darstellungen interpretierbar sind:
- Der Betrag $a(t)$ des äquivalentes TP–Signals $x_{\rm TP}(t)$ gibt die (zeitabhängige) Hüllkurve von $x(t)$ an.
- Die Phase $\phi(t)$ von $x_{\rm TP}(t)$ kennzeichnet die Lage der Nulldurchgänge von $x(t)$, wobei gilt:
- – Bei $\phi(t)>0$ ist der Nulldurchgang früher als seine Solllage ⇒ das Signal ist hier vorlaufend.
- – Bei $\phi(t)<0$ ist der Nulldurchgang später als seine Solllage ⇒ das Signal ist hier nachlaufend.
$\text{Beispiel 2:}$ Die Grafik soll diesen Zusammenhang verdeutlichen, wobei $A_{\rm U} > A_{\rm O}$ vorausgesetzt ist ⇒ der grüne Zeiger (für das untere Seitenband) ist länger als der blaue Zeiger (oberes Seitenband). Es handelt sich um eine Momentaufnahme zum Zeitpunkt $t_0$:
- Bei diesen Systemparametern liegt die Spitze des Zeigerverbundes $x_{\rm TP}(t)$ – also die geometrisch Summe aus rotem, blauem und grünem Zeiger – auf einer Ellipse.
- In der linken Grafik schwarz eingezeichnet ist der Betrag $a(t_0) = \vert x_{\rm TP}(t_0) \vert$ und in brauner Farbe angedeutet ist der Phasenwert $\phi(t_0) = \text{arc }x_{\rm TP}(t_0) > 0.$
- In der rechten Grafik gibt der Betrag $a(t_0) = \vert x_{\rm TP}(t_0) \vert$ des äquivalenten TP–Signals die Hüllkurve des physikalischen Signals $x(t)$ an.
- Bei $\phi(t) \equiv 0$ würden alle Nulldurchgänge von $x(t)$ in äquidistenten Abständen auftreten. Wegen $\phi(t_0) > 0$ ist zum Zeitpunkt $t_0$ das Signal vorlaufend, das heißt: Die Nulldurchgänge kommen früher, als es das Raster vorgibt.
Versuchsdurchführung
- Wählen Sie zunächst die Aufgabennummer.
- Eine Aufgabenbeschreibung wird angezeigt.
- Parameterwerte sind angepasst.
- Lösung nach Drücken von „Hide solition”.
Mit der Nummer „0” wird auf die gleichen Einstellung wie beim Programmstart zurückgesetzt und es wird ein Text mit weiteren Erläuterungen zum Applet ausgegeben.
Im Folgenden bezeichnet $\rm Grün$ das Untere Seitenband ⇒ $\big (A_{\rm U}, f_{\rm U}, \varphi_{\rm U}\big )$,
$\rm Rot$ den Träger ⇒ $\big (A_{\rm T}, f_{\rm T}, \varphi_{\rm T}\big )$ und
$\rm Blau$ das Obere Seitenband ⇒ $\big (A_{\rm O}, f_{\rm O}, \varphi_{\rm O}\big )$.
(1) Es gelte $\text{Rot:} \hspace{0.15cm} A_{\rm T} = 1\ \text{V}, f_{\rm T} = 100 \ \text{kHz}, \varphi_{\rm T} = 0^\circ$, $\text{Grün:} \hspace{0.15cm} A_{\rm U} = 0.4 \text{V}, \ f_{\rm U} = 80 \ \text{kHz}, \varphi_{\rm U} = -90^\circ$, $\text{Blau:} \hspace{0.15cm} A_{\rm O} = 0.4\ \text{V}, f_{\rm O} = 120 \ \text{kHz}, \varphi_{\rm O} = 90^\circ$.
- Betrachten und interpretieren Sie das äquivalente TP–Signal $x_{\rm TP}(t)$ und das physikalische Signal $x(t)$. Welche Periodendauer $T_0$ erkennt man?
- Das äquivalente TP–Signal $x_{\rm TP}(t)$ nimmt ausgehend von $x_{\rm TP}(t=0)=1\ \text{V}$ auf der reellen Achse Werte zwischen $0.2\ \text{V}$ und $1.8\ \text{V}$ an ⇒ Phase $\phi(t) \equiv 0$.
Der Betrag $|x_{\rm TP}(t)|$ gibt die Hüllkurve $a(t)$ des physikalischen Signals $x(t)$ an. Es gilt mit $A_{\rm N} = 0.8\ \text{V}$ und $f_{\rm N} = 20\ \text{kHz}$: $a(t) = A_{\rm T}+ A_{\rm N} \cdot \sin(2\pi\cdot f_{\rm N} \cdot t)$.
Sowohl $x_{\rm TP}(t)$ als auch $x(t)$ sind periodisch mit der Periodendauer $T_0 = 1/f_{\rm N} = 50\ \rm µ s$.
- Das äquivalente TP–Signal $x_{\rm TP}(t)$ nimmt ausgehend von $x_{\rm TP}(t=0)=1\ \text{V}$ auf der reellen Achse Werte zwischen $0.2\ \text{V}$ und $1.8\ \text{V}$ an ⇒ Phase $\phi(t) \equiv 0$.
(2) Wie ändern sich die Verhältnisse gegenüber (1) mit $f_{\rm U} = 99 \ \text{kHz}$ und $f_{\rm O} = 101 \ \text{kHz}$ ? Wie könnte $x(t)$ entstanden sein?
- Für die Hüllkurve $a(t)$ des Signals $x(t)$ gilt weiterhin $a(t) = A_{\rm T}+ A_{\rm N} \cdot \sin(2\pi\cdot f_{\rm N} \cdot t)$, aber nun mit $f_{\rm N} = 1\ \text{kHz}$. Auch wenn es nicht zu erkennen ist:
$x_{\rm TP}(t)$ und $x(t)$ sind weiterhin periodisch: $T_0 = 1\ \rm ms$. Beispiel: Zweiseitenband–Amplitudenmodulation (ZSB–AM) eines Sinussignals mit Cosinus–Träger.
- Für die Hüllkurve $a(t)$ des Signals $x(t)$ gilt weiterhin $a(t) = A_{\rm T}+ A_{\rm N} \cdot \sin(2\pi\cdot f_{\rm N} \cdot t)$, aber nun mit $f_{\rm N} = 1\ \text{kHz}$. Auch wenn es nicht zu erkennen ist:
(3) Welche Einstellungen müssen gegenüber (2) geändert werden, um zur ZSB–AM eines Cosinussignals mit Sinus–Träger zu gelangen. Was ändert sich gegenüber (2)?
- Die Trägerphase muss auf $\varphi_{\rm T} = 90^\circ$ geändert werden ⇒ Sinus–Träger. Ebenso muss $\varphi_{\rm O} =\varphi_{\rm U} =\varphi_{\rm T} = 90^\circ$ eingestellt werden ⇒ cosinusförmige Nachricht
Die Ortskurve liegt nun auf der imaginären Achse ⇒ $\phi(t) \equiv -90^\circ$. Zu Beginn gilt $x_{\rm TP}(t=0)= - {\rm j} \cdot 1.8 \ \text{V}$.
- Die Trägerphase muss auf $\varphi_{\rm T} = 90^\circ$ geändert werden ⇒ Sinus–Träger. Ebenso muss $\varphi_{\rm O} =\varphi_{\rm U} =\varphi_{\rm T} = 90^\circ$ eingestellt werden ⇒ cosinusförmige Nachricht
(4) Nun gelte $\text{Rot:} \hspace{0.15cm} A_{\rm T} = 1\ \text{V}, \ f_{\rm T} = 100 \ \text{kHz}, \ \varphi_{\rm T} = 0^\circ$, $\text{Grün:} \hspace{0.15cm} A_{\rm U} = 0.4 \text{V}, \ f_{\rm U} = 80 \ \text{kHz}, \ \varphi_{\rm U} = 0^\circ$, $\text{Blau:} \hspace{0.15cm} A_{\rm O} = 0.4\ \text{V}, \ f_{\rm O} = 120 \ \text{kHz}, \ \varphi_{\rm O} = 0^\circ$.
- Welche Eigenschaften weist dieses System „ZSB–AM, wobei Nachrichtensignal und Träger jeweils cosinusförmig” auf? Wie groß ist der Modulationsgrad $m$?
- Das äquivalente TP–Signal $x_{\rm TP}(t)$ nimmt ausgehend von $x_{\rm TP}(t=0)=1.8\ \text{V}$ auf der reellen Achse Werte zwischen $0.2\ \text{V}$ und $1.8\ \text{V}$ an ⇒ Phase $\phi(t) \equiv 0$.
Bis auf den Startzustand $x_{\rm TP}(t=0)$ gleiches Verhalten wie bei der Einstellung (1). Der Modulationsgrad ist jeweils $m = 0.8$.
- Das äquivalente TP–Signal $x_{\rm TP}(t)$ nimmt ausgehend von $x_{\rm TP}(t=0)=1.8\ \text{V}$ auf der reellen Achse Werte zwischen $0.2\ \text{V}$ und $1.8\ \text{V}$ an ⇒ Phase $\phi(t) \equiv 0$.
(5) Es gelten weiter die Parameter gemäß (4) mit Ausnahme von $A_{\rm T}= 0.6 \text{V}$. Wie groß ist nun der Modulationsgrad $m$? Welche Konsequenzen hat das?
- Es liegt nun eine ZSB–AM mit Modulationsgrad $m = 1.333$ vor. Bei $m > 1$ ist die einfachere Hüllkurvendemodulation nicht anwendbar, da nun die Phasenfunktion $\phi(t) \in \{ 0, \ \pm 180^\circ\}$ nicht mehr konstant ist und die Hüllkurve $a(t)$ nicht mehr mit dem Nachrichtensignal übereinstimmt. Vielmehr muss die aufwändigere Synchrondemodulation verwendet werden. Bei Hüllkurvendemodulation käme es zu nichtlinearen Verzerrungen.
(6) Es gelten weiter die Parameter gemäß (4) bzw. (5) mit Ausnahme von $A_{\rm T}= 0$ an ⇒ $m \to \infty$. Welches Modulationsverfahren wird so beschrieben?
- Es handelt sich um eine ZSB–AM ohne Träger und es ist eine eine Synchrondemodulation erforderlich. Das äquivalente TP–Signal $x_{\rm TP}(t)$ liegt zwar auf der reellen Achse, aber nicht nur in der rechten Halbebene. Damit gilt auch hier für die Phasenfunktion $\phi(t) \in \{ 0, \ \pm 180^\circ\}$, wodurch Hüllkurvendemodulation nicht anwendbar ist.
(7) Nun gelte $\text{Rot:} \hspace{0.15cm} A_{\rm T} = 1\ \text{V}, f_{\rm T} = 100 \ \text{kHz}, \varphi_{\rm T} = 0^\circ$, $\text{Grün:} \hspace{0.15cm} A_{\rm U} = 0, \ f_{\rm U} = 80 \ \text{kHz}, \varphi_{\rm U} = -90^\circ$, $\text{Blau:} \hspace{0.15cm} A_{\rm O} = 0.8\ \text{V}, f_{\rm O} = 120 \ \text{kHz}, \varphi_{\rm O} = 90^\circ$.
- Welches Konstellation wird hiermit beschrieben? Welche Eigenschaften dieses Verfahrens erkennt man aus der Grafik?
- Es handelt es sich um eine Einseitenbandmodulation (ESB–AM), genauer gesagt um eine OSB–AM: Der rote Träger liegt fest, der grüne Zeiger fehlt und der blaue Zeiger (OSB) dreht entgegen dem Uhrzeigersinn. Der Modulationsgrad ist $\mu = 0.8$ (bei ESB bezeichnen wir den Modulationsgrad mit $\mu$ anstelle von $m$). Das Trägersignal ist cosinusförmig und das Nachrichtensignal sinusförmig.
Die Ortskurve ist ein Kreis. $x_{\rm TP}(t)$ bewegt sich darauf in mathematisch positiver Richtung. Wegen $\phi(t) \ne \text{const.}$ ist auch hier die Hüllkurvendemodulation nicht anwendbar: Dies erkennt man daran, dass die Hüllkurve $a(t)$ nicht cosinusförmig ist. Vielmehr ist die untere Halbwelle spitzer als die obere ⇒ starke lineare Verzerrungen.
- Es handelt es sich um eine Einseitenbandmodulation (ESB–AM), genauer gesagt um eine OSB–AM: Der rote Träger liegt fest, der grüne Zeiger fehlt und der blaue Zeiger (OSB) dreht entgegen dem Uhrzeigersinn. Der Modulationsgrad ist $\mu = 0.8$ (bei ESB bezeichnen wir den Modulationsgrad mit $\mu$ anstelle von $m$). Das Trägersignal ist cosinusförmig und das Nachrichtensignal sinusförmig.
(8) Es gelten weiter die Parameter gemäß (7) mit Ausnahme von $A_{\rm O}= 0$ und $A_{\rm U}= 0.8 \text{V}$. Welche Unterschiede ergeben sich gegenüber (7)?
- Nun handelt es sich um eine USB–AM: Der rote Träger liegt fest, der blaue Zeiger fehlt und der grüne Zeiger (USB) dreht im Uhrzeigersinn. Alle anderen Aussagen von (7) treffen auch hier zu.
(9) Es gelten weiter die Parameter gemäß (7) mit Ausnahme von $A_{\rm O} = 0.2 \text{ V} \ne A_{\rm U} = 0.4 \text{ V} $. Welche Unterschiede ergeben sich gegenüber (7)?
- Die Ortskurve $x_{\rm TP}(t)$ ist nun keine horizontale Gerade, sondern eine Ellipse mit dem Realteil zwischen $0.4 \text{ V}$ und $1.6 \text{ V}$ sowie dem Imaginärteil im Bereich $\pm 0.2 \text{ V}$. Wegen $\phi(t) \ne \text{const.}$ würde auch hier die Hüllkurvendemodulation zu nichtlinearen Verzerrungen führen
Die hier simulierte Konstellation beschreibt die Situation von (4), nämlich eine ZSB–AM mit Modulationsgrad $m = 0.8$, wobei das obere Seitenband aufgrund der Kanaldämpfung auf $50\%$ reduziert wird.
- Die Ortskurve $x_{\rm TP}(t)$ ist nun keine horizontale Gerade, sondern eine Ellipse mit dem Realteil zwischen $0.4 \text{ V}$ und $1.6 \text{ V}$ sowie dem Imaginärteil im Bereich $\pm 0.2 \text{ V}$. Wegen $\phi(t) \ne \text{const.}$ würde auch hier die Hüllkurvendemodulation zu nichtlinearen Verzerrungen führen
Zur Handhabung des Applets
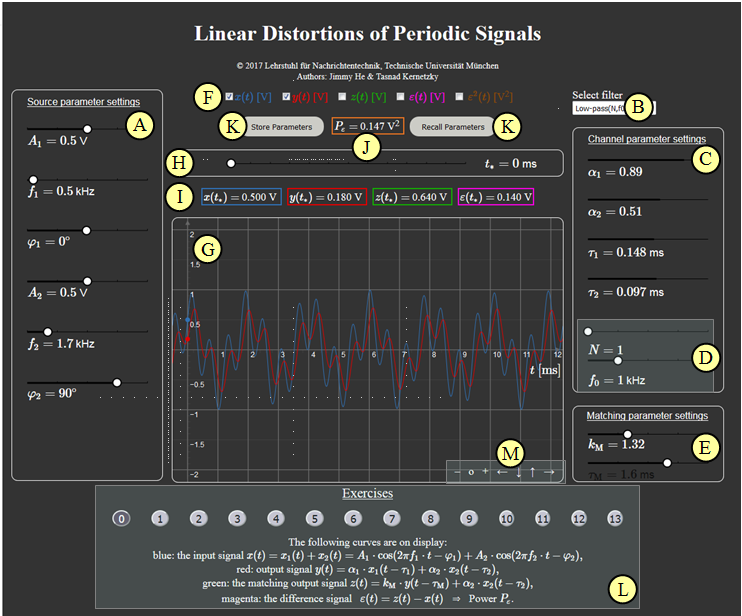
(A) Parametereingabe für das Eingangssignal $x(t)$ per Slider: Amplituden, Frequenzen, Phasenwerte
(B) Vorauswahl für die Kanalparameter: per Slider, Tiefpass oder Hochpass
(C) Eingabe der Kanalparameter per Slider: Dämpfungsfaktoren und Phasenlaufzeiten
(D) Eingabe der Kanalparameter für Hoch– und Tiefpass: Ordnung $n$, Grenzfrequenz $f_0$
(E) Eingabe der Matching–Parameter $k_{\rm M}$ und $\varphi_{\rm M}$
(F) Auswahl der darzustellenden Signale: $x(t)$, $y(t)$, $z(t)$, $\varepsilon(t)$, $\varepsilon^2(t)$
(G) Graphische Darstellung der Signale
(H) Eingabe der Zeit $t_*$ für die Numerikausgabe
( I ) Numerikausgabe der Signalwerte $x(t_*)$, $y(t_*)$, $z(t_*)$ und $\varepsilon(t_*)$
(J) Numerikausgabe des Hauptergebnisses $P_\varepsilon$
(K) Abspeichern und Zurückholen von Parametersätzen
(L) Bereich für die Versuchsdurchführung: Aufgabenauswahl, Aufgabenstellung und Musterlösung
(M) Variationsmöglichkeiten für die grafische Darstellung
$\hspace{1.5cm}$Zoom–Funktionen „$+$” (Vergrößern), „$-$” (Verkleinern) und $\rm o$ (Zurücksetzen)
$\hspace{1.5cm}$Verschieben mit „$\leftarrow$” (Ausschnitt nach links, Ordinate nach rechts), „$\uparrow$” „$\downarrow$” und „$\rightarrow$”
$\hspace{1.5cm}$Andere Möglichkeiten:
$\hspace{1.5cm}$Gedrückte Shifttaste und Scrollen: Zoomen im Koordinatensystem,
$\hspace{1.5cm}$Gedrückte Shifttaste und linke Maustaste: Verschieben des Koordinatensystems.
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2005 von Ji Li im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2018 wurde dieses Programm von Xiaohan Liu im Rahmen ihrer Bachelorarbeit (Betreuer: Tasnád Kernetzky) neu gestaltet und erweitert.