Aufgaben:Exercise 1.2Z: Sets of Digits

• Return to book

Ziffernmengen $A$, $B$, $C$

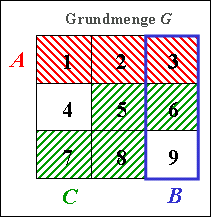
Die Grundmenge $G$ sei die Menge aller Ziffern zwischen $1$ und $9$. Gegeben sind dazu die folgenden Teilmengen:

$$A = \big[\text{die Ziffern} \leqslant 3\big],$$

$$ B = \big[\text{die durch 3 teilbaren Ziffern}\big],$$

$$ C = \big[\text{die Ziffern 5, 6, 7, 8}\big],$$

Daneben seien noch weitere Mengen definiert:

$$D = (A \cap \overline B) \cup (\overline A \cap B),$$

$$E = (A \cup B) \cap (\overline A \cup \overline B), $$

$$F = (A \cup C) \cap \overline B, $$

$$G = (\overline A \cap \overline C) \cup (A \cap B \cap C).$$

Überlegen Sie sich zunächst, welche Ziffern zu den Mengen $D$, $E$, $F$ und $H$ gehören und beantworten Sie dann die folgenden Fragen.
Begründen Sie Ihre Antworten mengentheoretisch.

Hinweise:

• Die Aufgabe gehört zum Kapitel Mengentheoretische Grundlagen.

• Eine Zusammenfassung der theoretischen Grundlagen mit Beispielen bringt das Lernvideo Mengentheoretische Begriffe und Gesetzmäßigkeiten.

Fragebogen

1

Welche der nachfolgenden Aussagen sind richtig?

	$A$ und $B$ sind disjunkte Mengen.
	$A$ und $C$ sind disjunkte Mengen.
	$B$ und $C$ sind disjunkte Mengen.

2

Welche der nachfolgenden Aussagen sind richtig?

	Die Vereinigungsmenge $A \cup B \cup C$ ergibt die Grundmenge $G$.
	Die Komplementärmenge zu $A \cap B \cap C$ ergibt die Grundmenge $G$.

3

Welche der nachfolgenden Aussagen sind richtig?

	Die Komplementärmengen von $D$ und $E$ sind identisch.
	$F$ ist eine Teilmenge der Komplementärmenge von $B$.
	Die Mengen $B$, $C$ und $D$ bilden ein vollständiges System.
	Die Mengen $A$, $C$ und $H$ bilden ein vollständiges System.

Musterlösung

Solution

Für die weiteren in der Aufgabe definierten Mengen gilt:

$$ D = (A \cap \overline B) \cup (\overline A \cap B) =\big[\{1, 2, 3\} \cap \{1, 2, 4, 5, 7, 8\}\big] \cup \big[\{4, 5, 6, 7, 8, 9\} \cap \{3, 6, 9\}\big] = \{1, 2, 6, 9\},$$

$$ E = (A \cup B) \cap (\overline A \cup \overline B) = (A \cap \overline A) \cup (A \cap \overline B) \cup (\overline A \cap B) \cup (\overline A \cap \overline B) = (A \cap \overline B) \cup (\overline A \cap B) = D = \{1, 2, 6, 9\},$$

$$F = (A \cup C= \cap \overline B = \{1, 2, 3, 5, 6, 7, 8\} \cap \{1, 2, 4, 5, 7, 8\} = \{1, 2, 5, 7, 8\},$$

$$H = (\bar A \cap \overline C) \cup (A \cap B \cap C) = (\overline A \cap \overline C) \cup \phi = \{4, 9\}.$$

(1)  Richtig ist nur der Lösungsvorschlag 2:

• $A$ und $C$ haben kein gemeinsames Element.
• $A$ und $B$ beinhalten jeweils die $3$.
• $B$ und $C$ beinhalten jeweils die $6$.

(2)  Richtig ist der Lösungsvorschlag 2:

• Keine Ziffer ist gleichzeitig in $A$, $B$ und $C$ enthalten   ⇒   $ A \cap B \cap C = \phi$   ⇒   $ \overline{A \cap B \cap C} = \overline{\phi} = G$.
• Der erste Vorschlag ist dagegen falsch. Es fehlt die $4$.

(3)  Richtig sind die Lösungsvorschläge 1, 2 und 4:

• Der erste Vorschlag ist richtig:   Die Mengen $D$ und $E$ enthalten genau die gleichen Elemente und somit auch deren Komplementärmengen.
• Auch der zweite Vorschlag ist richtig:   Allgemein, das heißt für beliebige $X$ und $B$ gilt: $X \cap \bar B \subset \bar B \ \Rightarrow$   Mit $X = A \cup C$ folgt somit $F \subset \bar B$.
• Auch der letzte Vorschlag ist richtig:   $A = \{1, 2, 3\},$ $C = \{5, 6, 7, 8\}$ und $H = \{4, 9\}$ bilden ein „vollständiges System”.
• Der dritte Vorschlag ist dagegen falsch, weil $B$ und $C$ nicht disjunkt sind.