Aufgaben:Exercise 2.3: Algebraic Sum of Binary Numbers

• Return to book

Summe von Binärzahlen

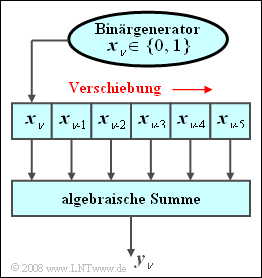
Ein Zufallsgenerator gibt zu jedem Taktzeitpunkt ($\nu$) eine binäre Zufallszahl $x_\nu$ ab, die $0$ oder $1$ sein kann.

• Der Wert „1” tritt mit Wahrscheinlichkeit $p = 0.25$ auf.
• Die einzelnen Werte $x_\nu$ seien statistisch voneinander unabhängig.

Die Binärzahlen werden in ein Schieberegister mit $I = 6$ Speicherzellen abgelegt.

Zu jedem Taktzeitpunkt wird der Inhalt dieses Schieberegisters um eine Stelle nach rechts verschoben und jeweils die algebraische Summe $y_\nu$ der Schieberegisterinhalte gebildet:

$$y_{\nu}=\sum\limits_{i=0}^{5}x_{\nu-i}=x_{\nu}+x_{\nu-1}+\ \text{...} \ +x_{\nu-5}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Binomialverteilung.

• Zur Kontrolle Ihrer Ergebnisse können Sie das interaktive Applet Binomial– und Poissonverteilung benutzen.

Fragebogen

1

Welche Werte kann die Summe $y$ annehmen? Was ist der größtmögliche Wert?

$y_\max \ = \ $

2

Berechnen Sie die Wahrscheinlichkeit, dass $y$ größer als $2$ ist.

${\rm Pr}(y > 2) \ = \ $

3

Wie groß ist der Mittelwert der Zufallsgröße $y$?

$m_y \ =$

4

Ermitteln Sie die Streuung der Zufallsgröße $y$.

$\sigma_y \ = \ $

5

Sind die Zufallszahlen $y_\nu$ unabhängig? Begründen Sie Ihr Ergebnis.

	Die Zufallszahlen sind statistisch unabhängig.
	Die Zufallszahlen sind statistisch abhängig.

6

Wie groß ist die bedingte Wahrscheinlichkeit, dass $y_\nu$ wieder gleich $\mu$ ist, wenn vorher $y_{\nu-1} = \mu$ aufgetreten ist? ($\mu = 0,1, \ \text{...} \ , I$).

${\rm Pr}(y_\nu = \mu \hspace{0.05cm} | \hspace{0.05cm} y_{\nu-1} = \mu ) \ = \ $

Musterlösung

Solution

(1)  In jeder Zelle kann eine $0$ oder eine $1$ stehen; deshalb kann die Summe alle ganzzahligen Werte zwischen $0$ und $6$ annehmen:

$$y_{\nu}\in\{0,1,\ \text{...} \ ,6\}\hspace{0.3cm}\Rightarrow\hspace{0.3cm} y_{\rm max} \hspace{0.15cm} \underline{= 6}.$$

(2)  Es liegt eine Binomialverteilung vor. Daher gilt mit $p = 0.25$:

$${\rm Pr}(y =0)=(1-p)^{\it I}=0.75^6=0.178,$$

$${\rm Pr}(y=1)=\left({ I \atop {1}}\right)\cdot (1-p)^{I-1}\cdot p= \rm 6\cdot 0.75^5\cdot 0.25=0.356,$$

$${\rm Pr}(y=2)=\left({ I \atop { 2}}\right)\cdot (1-p)^{I-2}\cdot p^{\rm 2}= \rm 15\cdot 0.75^4\cdot 0.25^2=0.297,$$

$$\Rightarrow \hspace{0.3cm}{\rm Pr}(y>2)=1-{\rm Pr}(y=0)-{\rm Pr}( y=1)-{\rm Pr}( y=2)\hspace{0.15cm} \underline{=\rm 0.169}.$$

(3)  Nach der allgemeinen Gleichung gilt für den Mittelwert der Binomialverteilung:

$$m_y= I\cdot p\hspace{0.15cm} \underline{=\rm 1.5}.$$

(4)  Entsprechend gilt für die Streuung der Binomialverteilung:

$$\sigma_y=\sqrt{ I \cdot p \cdot( 1- p)} \hspace{0.15cm} \underline{= \rm 1.061}.$$

(5)  Richtig ist der Lösungsvorschlag 2:

• Ist $y_\nu = 0$, so können zum nächsten Zeitpunkt nur die Werte $0$ und $1$ folgen, nicht aber $2$, ... , $6$.
• Das heißt:   Die Folge $ \langle y_\nu \rangle$ weist (starke) statistische Bindungen auf.

(6)  Die gesuchte Wahrscheinlichkeit ist identisch mit der Wahrscheinlichkeit dafür, dass das neue Binärsymbol gleich dem aus dem Schieberegister herausgefallenen Symbol ist. Daraus folgt:

$${\rm Pr} (y_{\nu} = \mu\hspace{0.05cm}| \hspace{0.05cm} y_{\nu-{1}} = \mu) = {\rm Pr}(x_{\nu}= x_{\nu-6}). $$

Da die Symbole $x_\nu$ statistisch voneinander unabhängig sind, kann hierfür auch geschrieben werden:

$${\rm Pr}(x_{\nu} = x_{\nu-6}) = {\rm Pr}\big[(x_{\nu}= 1)\hspace{0.05cm}\cap\hspace{0.05cm}(x_{\nu-6}= 1)\hspace{0.05cm}\cup \hspace{0.05cm}(x_\nu=0)\hspace{0.05cm}\cap\hspace{0.05cm}(x_{\nu-6} =0)\big]= p^{2}+(1- p)^{2}=\rm 0.25^2 + 0.75^2\hspace{0.15cm} \underline{ = 0.625}. $$