Difference between revisions of "Exercise 2.6Z: PN Generator of Length 3"
| Line 35: | Line 35: | ||
| − | {Ermitteln Sie die Ausgangsfolge $〈z_ν\rangle$ für die Zeitpunkte $1$, ... , $P$. Wie lauten die ersten 15 Binärwerte der Ausgangsfolge? ''Hinweis:'' Bezeichnen Sie die Zellen von links nach rechts mit $S_1$, $S_2$ und $S_3$. Ausgegeben wird der Wert $z_ν$, der zum Zeitpunkt $\nu$ in die Speicherzelle $S_1$ eingetragen wird. | + | {Ermitteln Sie die Ausgangsfolge $〈z_ν\rangle$ für die Zeitpunkte $1$, ... , $P$. Wie lauten die ersten 15 Binärwerte der Ausgangsfolge? <br>''Hinweis:'' Bezeichnen Sie die Zellen von links nach rechts mit $S_1$, $S_2$ und $S_3$. Ausgegeben wird der Wert $z_ν$, der zum Zeitpunkt $\nu$ in die Speicherzelle $S_1$ eingetragen wird. |
|type="()"} | |type="()"} | ||
- $1\ 0 \ 0 \ 1 \ 1 \ 0 \ 1 \ 0 \ 1 \ 1 \ 1 \ 1 \ 0 \ 0 \ 0$ . . . | - $1\ 0 \ 0 \ 1 \ 1 \ 0 \ 1 \ 0 \ 1 \ 1 \ 1 \ 1 \ 0 \ 0 \ 0$ . . . | ||
| Line 61: | Line 61: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | [[File:P_ID107__Sto_Z_2_6b.png|right|PN–Generator mit Oktalkennung 15]] | + | [[File:P_ID107__Sto_Z_2_6b.png|right|frame|PN–Generator mit Oktalkennung $15$]] |
'''(1)''' Es handelt sich um eine M-Sequenz mit $L= 3$. Daraus folgt $P= 2^L - 1 \hspace{0.15cm}\underline{= 7}$. | '''(1)''' Es handelt sich um eine M-Sequenz mit $L= 3$. Daraus folgt $P= 2^L - 1 \hspace{0.15cm}\underline{= 7}$. | ||
| + | |||
'''(2)''' Wir bezeichnen die Zellen von links nach rechts mit $S_1$, $S_2$ und $S_3$. Dann gilt: | '''(2)''' Wir bezeichnen die Zellen von links nach rechts mit $S_1$, $S_2$ und $S_3$. Dann gilt: | ||
| Line 73: | Line 74: | ||
Das Ergebnis ist in der ersten Zeile obiger Tabelle (rot markiert) eingetragen: | Das Ergebnis ist in der ersten Zeile obiger Tabelle (rot markiert) eingetragen: | ||
*Zum Taktzeitpunkt $\nu = 7$ ergibt sich die gleiche Speicherbelegung wie zum Zeitpunkt $\nu = 0$. | *Zum Taktzeitpunkt $\nu = 7$ ergibt sich die gleiche Speicherbelegung wie zum Zeitpunkt $\nu = 0$. | ||
| − | *Daraus folgt $ {P = 7}$ und die Folge lautet ab $\nu = 1$ entsprechend dem <u> | + | *Daraus folgt $ {P = 7}$ und die Folge lautet ab $\nu = 1$ entsprechend dem <u>Lösungsvorschlag 3</u> : |
| − | :$$\langle z_\nu \rangle = 1 \ 1 \ 0 \ 0 \ 1 \ 0 \ 1 \ 1 \ 1 \ 0 \ 0 \ 1 \ 0 \ 1 \ 1 \ ...$$ | + | :$$\langle z_\nu \rangle = 1 \ 1 \ 0 \ 0 \ 1 \ 0 \ 1 \ 1 \ 1 \ 0 \ 0 \ 1 \ 0 \ 1 \ 1 \ \text{...}$$ |
| − | Dagegen beschreibt Vorschlag 1 die M-Sequenz des PN-Generators mit Länge $L=4$ und Kennung $(31)$ ⇒ Periodenlänge ist $P= 15$. Beim Vorschlag 2 ist die Periodenläng $P= 4$ zu kurz. | + | *Dagegen beschreibt Vorschlag 1 die M-Sequenz des PN-Generators mit Länge $L=4$ und Kennung $(31)$ ⇒ Periodenlänge ist $P= 15$. |
| + | *Beim Vorschlag 2 ist die Periodenläng $P= 4$ zu kurz. | ||
| − | Der letzte Vorschlag schließlich hätte zwar die gewünschte Periodenlänge $P= 7$, aber aus der Modulo-2-Addition von $S_2= 0$ und $S_3= 1$ (für $\nu = 0$) folgt zum nächsten Zeitpunkt ($\nu = 1$) zwingend: $S_1= 1$. Diese Eigenschaft zeigt die Folge 4 nicht. | + | *Der letzte Vorschlag schließlich hätte zwar die gewünschte Periodenlänge $P= 7$, aber aus der Modulo-2-Addition von $S_2= 0$ und $S_3= 1$ (für $\nu = 0$) folgt zum nächsten Zeitpunkt ($\nu = 1$) zwingend: $S_1= 1$. Diese Eigenschaft zeigt die Folge 4 nicht. |
| Line 87: | Line 89: | ||
| − | [[File: P_ID2897__Sto_Z_2_6d.png|right|PN–Generator mit Oktalkennung 13]] | + | [[File: P_ID2897__Sto_Z_2_6d.png|right|frame|PN–Generator mit Oktalkennung $13$]] |
'''(4)''' In nebenstehender Tabelle ist die Entstehung der PN–Folge beim reziproken Polynom $G_{\rm R}(D)$ eingetragen. Man erkennt, dass der <u>Lösungsvorschlag 2</u> zutrifft: | '''(4)''' In nebenstehender Tabelle ist die Entstehung der PN–Folge beim reziproken Polynom $G_{\rm R}(D)$ eingetragen. Man erkennt, dass der <u>Lösungsvorschlag 2</u> zutrifft: | ||
*Auch bei der reziproken Anordnung muss die Periodenlänge $P = 7$ gelten, so dass der Vorschlag 1 (mit $P = 15$) ausscheidet. | *Auch bei der reziproken Anordnung muss die Periodenlänge $P = 7$ gelten, so dass der Vorschlag 1 (mit $P = 15$) ausscheidet. | ||
*Der Vorschlag 3 ist nur eine um zwei Zeittakte verschobene Version der Ausgangsfolge von $(15)$. | *Der Vorschlag 3 ist nur eine um zwei Zeittakte verschobene Version der Ausgangsfolge von $(15)$. | ||
| − | *Dagegen ist im (richtigen) zweiten Vorschlag die Inverse von ...$ 1 \ 1 \ 0 \ 0 \ 1 \ 0 \ 1$ ... – also die Folge ...$ 1 \ 0 \ 1 \ 0 \ 0 \ 1 \ 1$ ... – enthalten, wenn auch mit einem Phasenversatz. | + | *Dagegen ist im (richtigen) zweiten Vorschlag die Inverse von ... $ 1 \ 1 \ 0 \ 0 \ 1 \ 0 \ 1$ ... – also die Folge ... $ 1 \ 0 \ 1 \ 0 \ 0 \ 1 \ 1$ ... – enthalten, wenn auch mit einem Phasenversatz. |
Revision as of 16:18, 7 August 2018
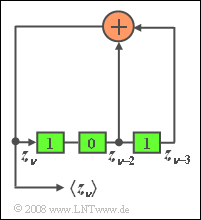
Nebenstehende Skizze zeigt einen PN-Generator der Länge $L = 3$ mit dem Generatorpolynom
- $$G( D) = D^{\rm 3} + D^{\rm 2} + \rm 1$$
und somit der Oktalkennung ($g_3 \ g_2 \ g_1 \ g_0$) = $(1 \ 1 \ 0 \ 1)_{\rm bin} = (15)_{\rm oct}$.
Das zugehörige reziproke Polynom $$G_{\rm R}(D) = D^{\rm 3} ( D^{\rm -3} + D^{\rm -2} + 1) = D^{\rm 3} + D^{\rm 1} + \rm 1$$
hat die Oktalkennung $(1 \ 0 \ 1 \ 1)_{\rm bin} = (13)_{\rm oct}$.
- Zum Startzeitpunkt seien die drei Speicherzellen mit den Binärwerten $1$, $0$ und $1$ vorbelegt.
- Beide Anordnungen erzeugen eine M-Sequenz.
Hinweise:
- Die Aufgabe gehört zum Kapitel Erzeugung von diskreten Zufallsgrößen.
- Wir verweisen hier auch auf das Lernvideo Erläuterung der PN-Generatoren an einem Beispiel.
Fragebogen
Musterlösung
(1) Es handelt sich um eine M-Sequenz mit $L= 3$. Daraus folgt $P= 2^L - 1 \hspace{0.15cm}\underline{= 7}$.
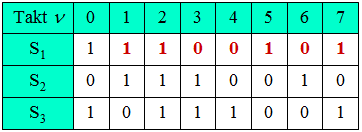
(2) Wir bezeichnen die Zellen von links nach rechts mit $S_1$, $S_2$ und $S_3$. Dann gilt:
- $S_2(\nu) = S_1(\nu - 1)$,
- $S_3(\nu) = S_2(\nu - 1)$,
- $S_1(\nu) = S_2(\nu - 1) \ {\rm mod } \ S_3(\nu - 1)$.
Das Ergebnis ist in der ersten Zeile obiger Tabelle (rot markiert) eingetragen:
- Zum Taktzeitpunkt $\nu = 7$ ergibt sich die gleiche Speicherbelegung wie zum Zeitpunkt $\nu = 0$.
- Daraus folgt $ {P = 7}$ und die Folge lautet ab $\nu = 1$ entsprechend dem Lösungsvorschlag 3 :
- $$\langle z_\nu \rangle = 1 \ 1 \ 0 \ 0 \ 1 \ 0 \ 1 \ 1 \ 1 \ 0 \ 0 \ 1 \ 0 \ 1 \ 1 \ \text{...}$$
- Dagegen beschreibt Vorschlag 1 die M-Sequenz des PN-Generators mit Länge $L=4$ und Kennung $(31)$ ⇒ Periodenlänge ist $P= 15$.
- Beim Vorschlag 2 ist die Periodenläng $P= 4$ zu kurz.
- Der letzte Vorschlag schließlich hätte zwar die gewünschte Periodenlänge $P= 7$, aber aus der Modulo-2-Addition von $S_2= 0$ und $S_3= 1$ (für $\nu = 0$) folgt zum nächsten Zeitpunkt ($\nu = 1$) zwingend: $S_1= 1$. Diese Eigenschaft zeigt die Folge 4 nicht.
(3) Richtig sind die Lösungsvorschläge 2, 3 und 4:
- Die maximale Anzahl aufeinander folgender Einsen ist $L$ (nämlich dann, wenn in allen $L$ Speicherzellen eine Eins steht).
- Es ist dagegen nicht möglich, dass alle Speicherzellen mit Nullen belegt sind. Deshalb gibt es stets eine Eins mehr als Nullen.
- Die Periodenlänge der letzten Folge beträgt $P = 2$. Bei einer M-Sequenz gilt dagegen $P= 2^L - 1.$ Für keinen Wert von $L$ ist $P = 2$ möglich.
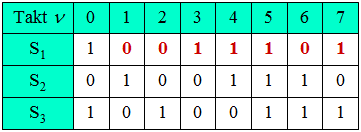
(4) In nebenstehender Tabelle ist die Entstehung der PN–Folge beim reziproken Polynom $G_{\rm R}(D)$ eingetragen. Man erkennt, dass der Lösungsvorschlag 2 zutrifft:
- Auch bei der reziproken Anordnung muss die Periodenlänge $P = 7$ gelten, so dass der Vorschlag 1 (mit $P = 15$) ausscheidet.
- Der Vorschlag 3 ist nur eine um zwei Zeittakte verschobene Version der Ausgangsfolge von $(15)$.
- Dagegen ist im (richtigen) zweiten Vorschlag die Inverse von ... $ 1 \ 1 \ 0 \ 0 \ 1 \ 0 \ 1$ ... – also die Folge ... $ 1 \ 0 \ 1 \ 0 \ 0 \ 1 \ 1$ ... – enthalten, wenn auch mit einem Phasenversatz.