Difference between revisions of "Aufgaben:Exercise 2.5Z: Compression Factor vs. Residual Redundancy"
From LNTwww
m (Textersetzung - „*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.“ durch „ “) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID2449__Inf_Z_2_5_neu.png|right| | + | [[File:P_ID2449__Inf_Z_2_5_neu.png|right|frame|Datenlänge $L(N)$ für zwei Quellen nach LZW–Codierung]] |
Wir betrachten wie in der [[Aufgaben:2.5_Restredundanz_bei_LZW-Codierung|Aufgabe 2.5]] die Datenkomprimierung mit dem 1983 veröffentlichten [[Informationstheorie/Komprimierung_nach_Lempel,_Ziv_und_Welch#Der_Lempel.E2.80.93Ziv.E2.80.93Welch.E2.80.93Algorithmus|Lempel–Ziv–Welch–Algorithmus]]. Dabei gilt: | Wir betrachten wie in der [[Aufgaben:2.5_Restredundanz_bei_LZW-Codierung|Aufgabe 2.5]] die Datenkomprimierung mit dem 1983 veröffentlichten [[Informationstheorie/Komprimierung_nach_Lempel,_Ziv_und_Welch#Der_Lempel.E2.80.93Ziv.E2.80.93Welch.E2.80.93Algorithmus|Lempel–Ziv–Welch–Algorithmus]]. Dabei gilt: | ||
| − | * Die Eingangsfolge habe die Länge | + | * Die Eingangsfolge habe die Länge $N$. |
| − | * Die Länge der LZW–Coderausgabe ist | + | * Die Länge der LZW–Coderausgabe ist $L$. |
| + | |||
| + | |||
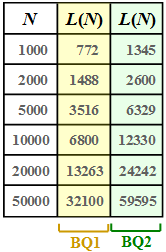
| + | Die Grafik zeigt für zwei verschiedene binäre Nachrichtenquellen $\rm BQ1$ und $\rm BQ2$ den Zusammenhang zwischen den Folgenlängen $N$ und $L$, dargestellt durch den Funktionsverlauf $L(N)$. Die beiden Nachrichtenquellen besitzen die gleichen statistischen Eigenschaften wie in der [[Aufgaben:Aufgabe_2.5:_Restredundanz_bei_LZW-Codierung|Aufgabe 2.5]]: | ||
| + | * $\rm BQ1$ ist aufgrund von ungleichen Symbolwahrscheinlichkeiten $(p_{\rm A} = 0.89$ und $p_{\rm B} = 0.11)$ redundant. Es bestehen keine Bindungen zwischen den einzelnen Symbolen. Die Entropie ist $H = 0.5$ bit/Quellensymbol. | ||
| + | * $\rm BQ2$ ist redundanzfrei und weist die Entropie $H = 1$ bit/Quellensymbol auf. | ||
| − | |||
| − | |||
| − | |||
Weiter benötigen Sie für die Lösung dieser Aufagbe noch zwei Definitionen: | Weiter benötigen Sie für die Lösung dieser Aufagbe noch zwei Definitionen: | ||
| − | * Der <i>Komprimierungsfaktor</i> ist definitionsgemäß | + | * Der <i>Komprimierungsfaktor</i> ist definitionsgemäß |
| + | :$$K(N) = \frac{L(N)}{N}\hspace{0.05cm}.$$ | ||
* Die relative Redundanz der LZW–Coderfolge (im Folgenden <i>Restredundanz</i> genannt) ist | * Die relative Redundanz der LZW–Coderfolge (im Folgenden <i>Restredundanz</i> genannt) ist | ||
:$$r(N) = \frac{L(N) - N \cdot H}{L(N)}= 1 - \frac{ N \cdot H}{L(N)}\hspace{0.05cm}.$$ | :$$r(N) = \frac{L(N) - N \cdot H}{L(N)}= 1 - \frac{ N \cdot H}{L(N)}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
*Die Aufgabe gehört zum Kapitel [[Informationstheorie/Komprimierung_nach_Lempel,_Ziv_und_Welch|Komprimierung nach Lempel, Ziv und Welch]]. | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Komprimierung_nach_Lempel,_Ziv_und_Welch|Komprimierung nach Lempel, Ziv und Welch]]. | ||
| − | *Insbesondere wird Bezug genommen auf die Seiten [[Informationstheorie/Komprimierung_nach_Lempel,_Ziv_und_Welch# | + | *Insbesondere wird Bezug genommen auf die Seiten |
| + | :: [[Informationstheorie/Komprimierung_nach_Lempel,_Ziv_und_Welch#Restredundanz_als_Ma.C3.9F_f.C3.BCr_die_Effizienz_von_Codierverfahren|Restredrundanz als Maß für die Effizienz von Codierverfahren]], | ||
| + | :: [[Informationstheorie/Komprimierung_nach_Lempel,_Ziv_und_Welch#Effizienz_der_Lempel.E2.80.93Ziv.E2.80.93Codierung|Effizienz der Lempel-Ziv-Codierung]] sowie | ||
| + | :: [[Informationstheorie/Komprimierung_nach_Lempel,_Ziv_und_Welch#Quantitative_Aussagen_zur_asymptotischen_Optimalit.C3.A4t|Quantitative Aussagen zur asymptotischen Optimalität]]. | ||
| Line 27: | Line 37: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welche Komprimierungfaktoren | + | {Welche Komprimierungfaktoren $K(N)$ ergeben sich mit $N = 10000$? |
|type="{}"} | |type="{}"} | ||
| − | + | $\rm BQ1$: $K(N = 10000) \ = \ $ { 0.68 3% } | |
| − | + | $\rm BQ2$: $K(N = 10000) \ = \ $ { 1.233 3% } | |
| − | {Wie groß ist die Restredundanz | + | {Wie groß ist die Restredundanz $r(N)$ (in Prozent)? Es gelte wieder $N = 10000$. |
|type="{}"} | |type="{}"} | ||
| − | + | $\rm BQ1$: $r(N = 10000) \ = \ $ { 26.5 3% } $\ \%$ | |
| − | + | $\rm BQ2$: $r(N = 10000) \ = \ $ { 19.0 3% } $\ \%$ | |
| − | {Welche Aussagen liefert der Vergleich von | + | {Welche Aussagen liefert der Vergleich von $N = 10000$ und $N = 50000$? |
|type="[]"} | |type="[]"} | ||
| − | + Bei beiden Quellen ist | + | + Bei beiden Quellen ist $K(N = 50000)$ kleiner als $K(N = 10000)$. |
| − | + Bei beiden Quellen ist | + | + Bei beiden Quellen ist $r(N = 50000)$ kleiner als $r(N = 10000)$. |
| − | - Nur bei | + | - Nur bei $\rm BQ1$ ergeben sich mit $N = 50000$ günstigere Werte. |
Revision as of 09:52, 26 September 2018
Wir betrachten wie in der Aufgabe 2.5 die Datenkomprimierung mit dem 1983 veröffentlichten Lempel–Ziv–Welch–Algorithmus. Dabei gilt:
- Die Eingangsfolge habe die Länge $N$.
- Die Länge der LZW–Coderausgabe ist $L$.
Die Grafik zeigt für zwei verschiedene binäre Nachrichtenquellen $\rm BQ1$ und $\rm BQ2$ den Zusammenhang zwischen den Folgenlängen $N$ und $L$, dargestellt durch den Funktionsverlauf $L(N)$. Die beiden Nachrichtenquellen besitzen die gleichen statistischen Eigenschaften wie in der Aufgabe 2.5:
- $\rm BQ1$ ist aufgrund von ungleichen Symbolwahrscheinlichkeiten $(p_{\rm A} = 0.89$ und $p_{\rm B} = 0.11)$ redundant. Es bestehen keine Bindungen zwischen den einzelnen Symbolen. Die Entropie ist $H = 0.5$ bit/Quellensymbol.
- $\rm BQ2$ ist redundanzfrei und weist die Entropie $H = 1$ bit/Quellensymbol auf.
Weiter benötigen Sie für die Lösung dieser Aufagbe noch zwei Definitionen:
- Der Komprimierungsfaktor ist definitionsgemäß
- $$K(N) = \frac{L(N)}{N}\hspace{0.05cm}.$$
- Die relative Redundanz der LZW–Coderfolge (im Folgenden Restredundanz genannt) ist
- $$r(N) = \frac{L(N) - N \cdot H}{L(N)}= 1 - \frac{ N \cdot H}{L(N)}\hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Komprimierung nach Lempel, Ziv und Welch.
- Insbesondere wird Bezug genommen auf die Seiten
Fragebogen
Musterlösung
(1) Der Komprimierungsfaktor ist definiert als der Quotient der Längen von LZW–Ausgangsfolge (L) und Eingangsfolge (N = 10000):
- $${\rm BQ1:}\hspace{0.3cm} K \hspace{0.2cm} = \hspace{0.2cm} \frac{6800}{10000}\hspace{0.15cm}\underline{= 0.680}\hspace{0.05cm},$$
- $$ {\rm BQ2:}\hspace{0.3cm} K \hspace{0.2cm} = \hspace{0.2cm} \frac{12330}{10000}\hspace{0.15cm}\underline{= 1.233}\hspace{0.05cm}. $$
- Die LZW–Codierung macht natürlich nur bei der redundanten Binärquelle BQ1 Sinn. Hier kann die Datenmenge um 32% gesenkt werden.
- Bei der redundanzfreien Binärquelle BQ2 führt dagegen die LZW–Codierung zu einer um 23.3% größeren Datenmenge.
(2) Aus der angegebenen Gleichung erhält man mit N = 10000:
- $${\rm BQ1:}\hspace{0.3cm} H = 0.5\hspace{0.05cm},\hspace{0.2cm} r(N=10000) \hspace{0.2cm} = \hspace{0.2cm}1 - \frac{0.5 \cdot N}{L } = 1 - \frac{5000}{6800 } \hspace{0.15cm}\underline{\approx 26.5\,\%}\hspace{0.05cm},$$
- $$ {\rm BQ2:}\hspace{0.3cm} H = 1.0\hspace{0.05cm},\hspace{0.2cm} r(N=10000) \hspace{0.2cm} = \hspace{0.2cm}1 - \frac{N}{L } = 1 - \frac{10000}{12330 } \hspace{0.15cm}\underline{\approx 19\,\%}\hspace{0.05cm}.$$
- Die Restredundanz gibt die (relative) Redundanz der LZWQ–Ausgangsfolge an.
- Obwohl die Quelle BQ1 für die LZW–Codierung besser geeignet ist als die redundanzfreie Quelle BQ2, ergibt sich bei BQ1 wegen der Redundanz in der Eingangsfolge eine größere Restredundanz.
- Eine kleinere Restredundanz r(N) bei gegebenem N sagt also nichts darüber aus, ob die LZW–Codierung für die vorliegende Quelle sinnvoll ist.
- Hierzu muss der Komprimierungsfaktor K betrachtet werden. Allgemein gilt folgender Zusammenhang zwischen r(N) und K(N):
- $$r(N) = 1 - \frac{H}{K(N)}\hspace{0.05cm},\hspace{0.2cm} K(N) = H \cdot (1- r(N)) \hspace{0.05cm}.$$
(3) Aus der Tabelle auf der Angabenseite kann man ablesen (bzw. daraus ableiten)
- für die redundante Binärquelle BQ1:
- $$L(N = 50000) = 32100\hspace{0.05cm},\hspace{0.2cm} K(N = 50000) = 0.642\hspace{0.05cm},\hspace{0.2cm}r(N = 50000) \hspace{0.15cm}\underline {= 22.2\,\% \hspace{0.05cm}},$$
- für die redundanzfreie Binärquelle BQ2:
- $$L(N = 50000) = 59595\hspace{0.05cm},\hspace{0.2cm} K(N = 50000) = 1.192\hspace{0.05cm},\hspace{0.2cm}r(N = 50000) \hspace{0.15cm}\underline {= 16.1\,\% \hspace{0.05cm}}.$$
Richtig sind somit die Aussagen 1 und 2:
- Für beide Quellen ist der Komprimierungsfaktor K(N) für N = 50000 kleiner als für N = 10000.
- Gleiches gilt für die Resrredundanz: r(N = 50000) ist kleiner als r(N = 10000).
- Sowohl hinsichtlich K(N) als auch hinsichtlich r(N) ergeben sich also bei größerem N „günstigere” Werte, auch dann, wenn eigentlich wie bei der redundanzfreien Binärquelle BQ2 die Anwendung von Lempel–Ziv zu einer Verschlechterung führt.