Aufgaben:Exercise 2.8: Huffman Application for a Markov Source

• Return to book

Symmetrische Markovquelle

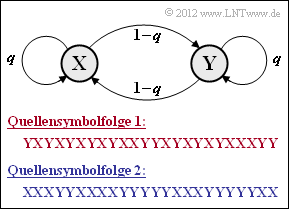
Wir betrachten hier die binäre symmetrische Markovquelle entsprechend nebenstehender Grafik, die durch den einzigen Parameter

$$q = {\rm Pr}(\boldsymbol{\rm X}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm X}) = {\rm Pr}(\boldsymbol{\rm Y}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm Y})$$

vollständig beschrieben wird.

• Die angegebenen Quellensymbolfolgen gelten für die bedingten Wahrscheinlichkeiten  $q = 0.2$  bzw.  $q = 0.8$.
• In der Teilaufgabe (1) ist zu klären, welche Symbolfolge – die rote oder die blaue – mit  $q = 0.2$  und welche mit  $q = 0.8$  generiert wurde.

Die Eigenschaften von Markovquellen werden im Kapitel Nachrichtenquellen mit Gedächtnis ausführlich beschrieben. Aufgrund der hier vorausgesetzten Symmetrie bezüglich der Binärsymbole  $\rm X$  und  $\rm Y$  ergeben sich einige gravierende Vereinfachungen, wie in der Zusatzaufgabe 1.5Z hergeleitet wird:

• Die Symbole  $\rm X$  und  $\rm Y$  sind gleichwahrscheinlich, das heißt, es ist $p_{\rm X} = p_{\rm Y} = 0.5$. Damit lautet die erste Entropienäherung:   $H_1 = 1\,\,{\rm bit/Quellensymbol}\hspace{0.05cm}.$
• Die Entropie der Markovquelle ergibt sich sowohl für  $q = 0.2$  als auch für  $q = 0.8$  zu

$$H = q \cdot {\rm log_2}\hspace{0.15cm}\frac{1}{q} + (1-q) \cdot {\rm log_2}\hspace{0.15cm}\frac{1}{1-q} = 0.722\,\,{\rm bit/Quellensymbol}\hspace{0.05cm}.$$

• Bei Markovquellen sind alle Entropienäherungen mit Ordnung $k \ge 2$ durch $H_1$ und $H = H_{k \to \infty}$ bestimmt. Die folgenden Zahlenwerte gelten wieder für  $q = 0.2$  und  $q = 0.8$  gleichermaßen:

$$H_2 = {1}/{2}\cdot \big [ H_1 + H \big ] = 0.861\,\,{\rm bit/Quellensymbol}\hspace{0.05cm},$$

$$H_3 = {1}/{3} \cdot \big [ H_1 + 2H \big ] = 0.815\,\,{\rm bit/Quellensymbol}\hspace{0.05cm}.$$

In dieser Aufgabe soll der Huffman–Algorithmus auf $k$–Tupel angewandt werden, wobei wir uns auf $k = 2$ und $k = 3$ beschränken.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Entropiecodierung nach Huffman.
• Insbesondere wird auf die Seite Anwendung der Huffman-Codierung auf k-Tupel Bezug genommen.
• Nützliche Informationen finden Sie auch in den Angabenblättern zu  Aufgabe 2.7  und  Aufgabe 2.7Z.
• Zur Kontrolle Ihrer Ergebnisse verweisen wir auf das Interaktionsmodul  Shannon–Fano– und Huffman–Codierung.

Fragebogen

1

Welche der vorne angegebenen Beispielfolgen gilt für $q = 0.8$?

	die rote Quellensymbolfolge 1,
	die blaue Quellensymbolfolge 2,

2

Welche der folgenden Aussagen treffen zu?

	Auch die direkte Anwendung von Huffman ist hier sinnvoll.
	Huffman macht bei Bildung von Zweiertupeln $(k = 2)$ Sinn.
	Huffman macht bei Bildung von Dreiertupeln $(k = 3)$ Sinn.

3

Wie lauten die Wahrscheinlichkeiten der Zweiertupel $(k = 2)$ für  $\underline{q = 0.8}$?

$p_{\rm A} = \rm Pr(XX)\ = \ $

$p_{\rm B} = \rm Pr(XY)\ = \ $

$p_{\rm C} = \rm Pr(YX)\ = \ $

$p_{\rm D} = \rm Pr(YY)\ = \ $

4

Ermitteln Sie mit dem angegebenen Flash–Modul den Huffman–Code für $\underline{k = 2}$.
Wie groß ist in diesem Fall die mittlere Codewortlänge?

$L_{\rm M} \ = \ $ $\ \rm bit/Quellensymbol$

5

Welche Schranke ergibt sich für die mittlere Codewortlänge, wenn Zweiertupel gebildet werden $(k = 2)$? Interpretation.

	$L_{\rm M} \ge H_1 = 1.000$ bit/Quellensymbol,
	$L_{\rm M} \ge H_2 \approx 0.861$ bit/Quellensymbol,
	$L_{\rm M} \ge H_3 \approx 0.815$ bit/Quellensymbol,
	$L_{\rm M} \ge H_{k \to \infty} \approx 0.722$ bit/Quellensymbol,
	$L_{\rm M} \ge 0.5$ bit/Quellensymbol.

6

Berechnen Sie die Wahrscheinlichkeiten der Dreiertupel $(k = 3)$ für  $\underline{q = 0.8}$?

$p_{\rm A} = \rm Pr(XXX)\ = \ $

$p_{\rm B} = \rm Pr(XXY)\ = \ $

$p_{\rm C} = \rm Pr(XYX)\ = \ $

$p_{\rm D} = \rm Pr(XYY)\ = \ $

$p_{\rm E} = \rm Pr(YXX)\ = \ $

$p_{\rm F} = \rm Pr(YXY)\ = \ $

$p_{\rm G} = \rm Pr(YYX)\ = \ $

$p_{\rm H} = \rm Pr(YYY)\ = \ $

7

Ermitteln Sie mit dem genannten Flash–Modul den Huffman–Code für $\underline{k = 3}$.
Wie groß ist in diesem Fall die mittlere Codewortlänge?

$L_{\rm M} \ = \ $ $\ \rm bit/Quellensymbol$

Musterlösung

Solution

(1)  Richtig ist der Lösungsvorschlag 2:

• Bei der blauen Quellensymbolfolge 2 erkennt man sehr viel weniger Symbolwechsel als in der roten Folge.
• Die Symbolfolge 2 wurde mit dem Parameter $q = {\rm Pr}(\boldsymbol{\rm X}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm X}) = {\rm Pr}(\boldsymbol{\rm Y}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm Y}) = 0.8$ erzeugt und die rote Symbolfolge 1 mit $q = 0.2$.

(2)  Richtig sind die Antworten 2 und 3.:

• Da hier die Quellensymbole $\rm X$ und $\rm X$ gleichwahrscheinlich angenommen wurden, macht die direkte Anwendung von Huffman keinen Sinn.
• Dagegen kann man die inneren statistischen Bindungen der Markovquelle zur Datenkomprimierung nutzen, wenn man $k$–Tupel bildet $(k ≥ 2)$.
• Je größer $k$ ist, desto mehr nähert sich die Codewortlänge $L_{\rm M}$ der Entropie $H$.

(3)  Die Symbolwahrscheinlichkeiten sind $p_{\rm X} = p_{\rm Y} = 0.5$. Damit erhält man für die Zweiertupel:

$$p_{\rm A} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XX}) = p_{\rm X} \cdot {\rm Pr}(\boldsymbol{\rm X}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm X}) = 0.5 \cdot q = 0.5 \cdot 0.8 \hspace{0.15cm}\underline{ = 0.4} \hspace{0.05cm},$$

$$p_{\rm B} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XY}) = p_{\rm X} \cdot {\rm Pr}(\boldsymbol{\rm Y}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm X}) = 0.5 \cdot (1-q)= 0.5 \cdot 0.2 \hspace{0.15cm}\underline{ = 0.1} \hspace{0.05cm},$$

$$p_{\rm C} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm YX}) = p_{\rm Y} \cdot {\rm Pr}(\boldsymbol{\rm X}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm Y}) = 0.5 \cdot (1-q)= 0.5 \cdot 0.2 \hspace{0.15cm}\underline{ = 0.1} \hspace{0.05cm},$$

$$p_{\rm D} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm YY}) = p_{\rm Y} \cdot {\rm Pr}(\boldsymbol{\rm Y}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm Y}) = 0.5 \cdot q = 0.5 \cdot 0.8\hspace{0.15cm}\underline{ = 0.4} \hspace{0.05cm}.$$

Zur Huffman–Codierung für $k = 2$

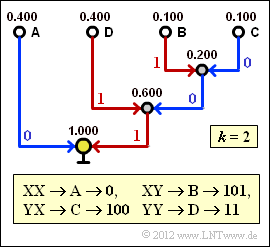
(4)  Nebenstehender Bildschirmabzug des Programms Shannon–Fano– und Huffman–Codierung zeigt die Konstruktion des Huffman–Codes für $k = 2$ mit den soeben berechneten Wahrscheinlichkeiten. Damit gilt für die mittlere Codewortlänge:

$$L_{\rm M}\hspace{0.01cm}' = 0.4 \cdot 1 + 0.4 \cdot 2 + (0.1 + 0.1) \cdot 3 = 1.8\,\,{\rm bit/Zweiertupel}$$

$$\Rightarrow\hspace{0.3cm}L_{\rm M} = {L_{\rm M}\hspace{0.01cm}'}/{2}\hspace{0.15cm}\underline{ = 0.9\,{\rm bit/Quellensymbol}}\hspace{0.05cm}.$$

(5)  Richtig iist der Lösungsvorschlag 2:

• Nach dem Quellencodierungstheorem gilt $L_{\rm M} ≥ H$.
• Wendet man aber Huffman–Codierung an und lässt dabei Bindungen zwischen nicht benachbarten Symbolen außer Betracht $(k = 2)$, so gilt als unterste Grenze der Codewortlänge nicht $H = 0.722$, sondern $H_2 = 0.861$ (auf den Zusatz bit/Quellensymbol wird für den Rest der Aufgabe verzichtet).
• Das Ergebnis der Teilaufgabe (4) war $L_{\rm M} = 0.9.$
• Würde eine unsymmetrische Markovkette vorliegen und zwar derart, dass sich für die Wahrscheinlichkeiten $p_{\rm A}$, ... , $p_{\rm D}$ die Werte $50\%$, $25\%$ und zweimal $12.5\%$ ergeben würden, so käme man auf die mittlere Codewortlänge $L_{\rm M} = 0.875$.
• Wie die genauen Parameter dieser unsymmetrischen Markovquelle aussehen, weiß aber auch der Aufgabensteller (G. Söder) nicht.
• Auch nicht, wie sich der Wert $0.875$ auf $0.861$ senken ließe. Der Huffman–Algorithmus ist hierfür jedenfalls ungeeignet.

(6)  Mit $q = 0.8$ und $1 - q = 0.2$ erhält man:

$$p_{\rm A} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XXX}) = 0.5 \cdot q^2 \hspace{0.15cm}\underline{ = 0.32} = p_{\rm H} = {\rm Pr}(\boldsymbol{\rm YYY})\hspace{0.05cm},$$

$$p_{\rm B} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XXY}) = 0.5 \cdot q \cdot (1-q) \hspace{0.15cm}\underline{ = 0.08}= p_{\rm G} = {\rm Pr}(\boldsymbol{\rm YYX}) \hspace{0.05cm},$$

$$p_{\rm C} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XYX}) = 0.5 \cdot (1-q)^2\hspace{0.15cm}\underline{ = 0.02} = p_{\rm F}= {\rm Pr}(\boldsymbol{\rm YXY}) \hspace{0.05cm},$$

$$p_{\rm D} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XYY}) = 0.5 \cdot (1-q) \cdot q \hspace{0.15cm}\underline{ = 0.08} = p_{\rm E} = {\rm Pr}(\boldsymbol{\rm YXX})\hspace{0.05cm}.$$

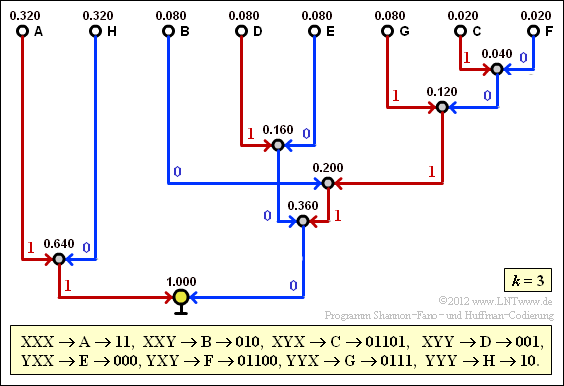
(7)  Der Bildschirmabzug des Flash–Moduls verdeutlicht die Konstellation des Huffman–Codes für $k = 3$. Damit erhält man für die mittlere Codewortlänge:

$$L_{\rm M}\hspace{0.01cm}' = 0.64 \cdot 2 + 0.24 \cdot 3 + 0.04 \cdot 5 = 2.52\,\,{\rm bit/Dreiertupel}\hspace{0.3cm} \Rightarrow\hspace{0.3cm}L_{\rm M} = {L_{\rm M}\hspace{0.01cm}'}/{3}\hspace{0.15cm}\underline{ = 0.84\,{\rm bit/Quellensymbol}}\hspace{0.05cm}.$$

Zur Huffman–Codierung für $k = 3$

• Man erkennt die Verbesserung gegenüber (4).
• Die für $k = 2$ gültige informationstheoretische Schranke $H_2 = 0.861$ wird nun von der mittleren Codewortlänge $L_{\rm M}$ unterschritten.
• Die neue Schranke für $k = 3$ ist $H_3 = 0.815$.
• Um die Quellenentropie $H = 0.722$ zu erreichen (besser gesagt: diesem Endwert bis auf ein $ε$ nahe zu kommen), müsste man allerdings unendlich lange Tupel bilden $(k → ∞)$.