Difference between revisions of "Aufgaben:Exercise 1.5Z: Sinc-shaped Impulse Response"
m (Textersetzung - „*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.“ durch „ “) |
|||
| Line 4: | Line 4: | ||
[[File:P_ID857__LZI_Z_1_5.png|right|frame|si–förmige Impulsantwort]] | [[File:P_ID857__LZI_Z_1_5.png|right|frame|si–förmige Impulsantwort]] | ||
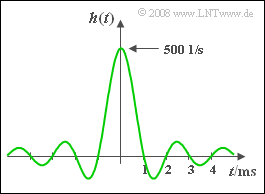
Die Impulsantwort eines linearen zeitinvarianten (und akausalen) Systems wurde wie folgt ermittelt (siehe Grafik): | Die Impulsantwort eines linearen zeitinvarianten (und akausalen) Systems wurde wie folgt ermittelt (siehe Grafik): | ||
| − | :$$h(t) = 500\hspace{0.1cm}{ {\rm s}}^{-1}\cdot{\rm si}[\pi | + | :$$h(t) = 500\hspace{0.1cm}{ {\rm s}}^{-1}\cdot{\rm si}\big[\pi |
| − | \cdot {t}/({ 1\hspace{0.1cm}{\rm ms}})] .$$ | + | \cdot {t}/({ 1\hspace{0.1cm}{\rm ms}})\big] .$$ |
Berechnet werden sollen die Ausgangssignale $y(t)$, wenn am Eingang verschiedene Cosinusschwingungen unterschiedlicher Frequenz $f_0$ angelegt werden: | Berechnet werden sollen die Ausgangssignale $y(t)$, wenn am Eingang verschiedene Cosinusschwingungen unterschiedlicher Frequenz $f_0$ angelegt werden: | ||
:$$x(t) = 4\hspace{0.05cm}{\rm V}\cdot {\rm cos}(2\pi \cdot f_0 | :$$x(t) = 4\hspace{0.05cm}{\rm V}\cdot {\rm cos}(2\pi \cdot f_0 | ||
| Line 16: | Line 16: | ||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Einige_systemtheoretische_Tiefpassfunktionen|Einige systemtheoretische Tiefpassfunktionen]]. | + | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Einige_systemtheoretische_Tiefpassfunktionen|Einige systemtheoretische Tiefpassfunktionen]]. |
| − | *Die Lösung kann | + | *Die Lösung kann im Zeitbereich oder im Frequenzbereich gefunden werden. In der Musterlösung finden Sie beide Lösungswege. |
| − | *Gegeben ist | + | *Gegeben ist das folgende bestimmte Integral: |
:$$\int_{ 0 }^{ \infty } \frac{\sin(u) \cdot \cos(a \cdot u)}{u} \hspace{0.15cm}{\rm | :$$\int_{ 0 }^{ \infty } \frac{\sin(u) \cdot \cos(a \cdot u)}{u} \hspace{0.15cm}{\rm | ||
d}u = \left\{ \begin{array}{c} \pi/2 \\ \pi/4 \\ 0 \\ \end{array} \right.\quad \quad | d}u = \left\{ \begin{array}{c} \pi/2 \\ \pi/4 \\ 0 \\ \end{array} \right.\quad \quad | ||
| Line 31: | Line 31: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Berechnen Sie den Frequenzgang $H(f)$ des LZI-Systems. Wie groß sind die äquivalente Bandbreite und der Gleichsignalübertragungsfaktor? | + | {Berechnen Sie den Frequenzgang $H(f)$ des LZI-Systems. <br>Wie groß sind die äquivalente Bandbreite und der Gleichsignalübertragungsfaktor? |
|type="{}"} | |type="{}"} | ||
$\Delta f \ =\ $ { 1 3% } $\ \rm kHz$ | $\Delta f \ =\ $ { 1 3% } $\ \rm kHz$ | ||
Revision as of 09:12, 6 November 2018
Die Impulsantwort eines linearen zeitinvarianten (und akausalen) Systems wurde wie folgt ermittelt (siehe Grafik):
- $$h(t) = 500\hspace{0.1cm}{ {\rm s}}^{-1}\cdot{\rm si}\big[\pi \cdot {t}/({ 1\hspace{0.1cm}{\rm ms}})\big] .$$
Berechnet werden sollen die Ausgangssignale $y(t)$, wenn am Eingang verschiedene Cosinusschwingungen unterschiedlicher Frequenz $f_0$ angelegt werden:
- $$x(t) = 4\hspace{0.05cm}{\rm V}\cdot {\rm cos}(2\pi \cdot f_0 \cdot t ) .$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Einige systemtheoretische Tiefpassfunktionen.
- Die Lösung kann im Zeitbereich oder im Frequenzbereich gefunden werden. In der Musterlösung finden Sie beide Lösungswege.
- Gegeben ist das folgende bestimmte Integral:
- $$\int_{ 0 }^{ \infty } \frac{\sin(u) \cdot \cos(a \cdot u)}{u} \hspace{0.15cm}{\rm d}u = \left\{ \begin{array}{c} \pi/2 \\ \pi/4 \\ 0 \\ \end{array} \right.\quad \quad \begin{array}{c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c}{ |a| < 1,} \\{ |a| = 1,} \\ { |a| > 1.} \\ \end{array}$$
Fragebogen
Musterlösung
- $$H(f) = \left\{ \begin{array}{c} \hspace{0.25cm}K \\ K/2 \\ 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.005cm} f\hspace{0.05cm} \right| < \Delta f/2,} \\ {\left| \hspace{0.005cm}f\hspace{0.05cm} \right| = \Delta f/2,} \\ {\left|\hspace{0.005cm} f \hspace{0.05cm} \right| > \Delta f/2.} \\ \end{array}$$
- Die äquidistanten Nulldurchgänge der Impulsantwort treten im Abstand $Δt = 1 \ \rm ms$ auf.
- Daraus folgt die äquivalente Bandbreite $Δf \rm \underline{ = 1 \ \rm kHz}$.
- Wäre $K = 1$, so müsste $h(0) = Δf = 1000 \cdot \rm 1/s$ gelten.
- Wegen der Angabe $h(0) = 500 \cdot{\rm 1/s} = Δf/2$ ist somit der Gleichsignalübertragungsfaktor $K = H(f = 0) \; \rm \underline{= 0.5}$.
(2) Diese Aufgabe lässt sich am einfachsten im Spektralbereich lösen. Für das Ausgangsspektrum gilt: $Y(f) = X(f)\cdot H(f) .$
- $X(f)$ besteht aus zwei Diracfunktionen bei $± f_0$, jeweils mit Gewicht $A_x/2 =2 \rm V$.
- Bei $f = f_0 = 1 \ {\rm kHz} > Δf/2$ ist aber $H(f) = 0$, so dass $Y(f) = 0$ und damit auch $y(t) = 0$ ist ⇒ $\underline{y(t = 0) = 0}$.
Die Lösung im Zeitbereich basiert auf der Faltung:
- $$y(t) = x (t) * h (t) = \int_{ - \infty }^{ + \infty } {h ( \tau )} \cdot x ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$
- Zum Zeitpunkt $t = 0$ erhält man unter Berücksichtigung der Symmetrie der Cosinusfunktion:
- $$y(t = 0 ) = \frac{A_x \cdot \Delta f}{2} \cdot \int_{ - \infty }^{ + \infty } {\rm si} ( \pi \cdot \Delta f \cdot \tau ) \cdot {\rm cos}(2\pi \cdot f_0 \cdot \tau ) \hspace{0.1cm}{\rm d}\tau.$$
- Mit der Substitution $u = π · Δf · τ$ kann hierfür auch geschrieben werden:
- $$y(t = 0 ) = \frac{A_x }{\pi} \cdot \int_{ 0 }^{ \infty } \frac{\sin(u) \cdot \cos(a \cdot u)}{u} \hspace{0.15cm}{\rm d}u .$$
Hierbei ist die Konstante $a = 2f_0/Δf = 2$. Mit diesem Wert liefert das angegebene Integral den Wert 0: $y(t = 0 ) = {A_y } = 0.$
(3) Der Frequenzgang bei $f = f_0 = 100 \ \rm Hz$ ist nach den Berechnungen zur Teilaufgabe (1) gleich $K = 0.5$. Deshalb ergibt sich
- $$A_y = A_x/2 = 2\ \rm V.$$
Zum gleichen Ergebnis kommt man über die Faltung nach obiger Gleichung. Für $a = 2f_0/Δf = 0.2$ ist das Integral gleich $π/2$ und man erhält
- $$y(t = 0 ) = {A_y } = \frac{A_x}{\pi} \cdot \frac{\pi}{2} = \frac{A_x}{2} \hspace{0.15cm}\underline{= 2\,{\rm V}}.$$
(4) Genau bei $f = 0.5 \ \rm kHz$liegt der Übergang vom Durchlass– zum Sperrbereich und es gilt für diese singuläre Stelle:
- $$H(f = f_0) = K/2.$$
Somit ist die Amplitude des Ausgangssignals nur halb so groß wie in der Teilaufgabe (3) berechnet, nämlich $A_y \; \underline{= 1 \ \rm V}$. Zum gleichen Ergebnis kommt man mit $a = 2f_0/Δf = 1$ über die Faltung.